はじめに
今回は量子振幅増幅と呼ばれる手法を解説し、その応用例としてグローバーのアルゴリズムを紹介する。グローバーのアルゴリズムは、ソートされていないデータベースから特定のデータを探索する手法であり、![]() 個のデータに対し
個のデータに対し![]() 回の問い合わせで目的とするデータを発見できる。古典コンピュータの場合、ソートされていないデータベースから目的のデータを見つけるには線形探索するしかなく、その問い合わせ回数は
回の問い合わせで目的とするデータを発見できる。古典コンピュータの場合、ソートされていないデータベースから目的のデータを見つけるには線形探索するしかなく、その問い合わせ回数は![]() である。したがって量子コンピュータを用いることで検索速度を加速させることができる。
である。したがって量子コンピュータを用いることで検索速度を加速させることができる。
量子振幅増幅
本節では量子振幅増幅について説明する。グローバーのアルゴリズムについては次節で解説する。
![]() 個の量子ビットからなる量子状態
個の量子ビットからなる量子状態![]() が次式で与えられているとする。
が次式で与えられているとする。
(1) 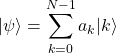
ここで、振幅![]() は複素数である。
は複素数である。![]() に対しては次の規格化条件が成り立っている。
に対しては次の規格化条件が成り立っている。
(2) 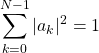
(3) ![]()
式(3)の2行目の式に見るように量子状態は2進数で表されることに注意する。いまの場合は2ビットの2進数である。また、式(2)より
(4) ![]()
が成り立つ。量子状態![]() を測定したとき、
を測定したとき、![]() が測定される確率が
が測定される確率が![]() となるのが量子力学の原理であった。
となるのが量子力学の原理であった。
さて、ある2値関数![]() が定義されているとき、
が定義されているとき、![]() となる量子状態
となる量子状態![]() を検索したい。それを行うため、式(1)の右辺を、
を検索したい。それを行うため、式(1)の右辺を、![]() を満たす状態
を満たす状態![]() と
と![]() を満たす状態
を満たす状態![]() に分ける。
に分ける。
(5) 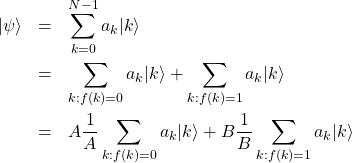
ここで
(6) 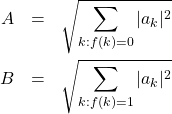
とした。いま
(7) 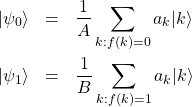
とし、さらに式(2)から
(8) ![]()
(9) ![]()
と書くことができる。2つのベクトル![]() と
と![]() に対し
に対し
(10) 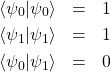
が成り立つことから(![]() は2つのベクトルの内積を表す)、2つのベクトル
は2つのベクトルの内積を表す)、2つのベクトル![]() が張る2次元ベクトル空間でアルゴリズムを考えることができる。ここでは
が張る2次元ベクトル空間でアルゴリズムを考えることができる。ここでは
(11) 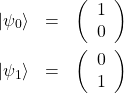
と置いて考える。いま見つけたいのは![]() となる状態である。つまり、
となる状態である。つまり、![]() の
の![]() 軸成分である
軸成分である![]() を増幅させれば良い。増幅の手順は以下の通り(下図参照)。
を増幅させれば良い。増幅の手順は以下の通り(下図参照)。
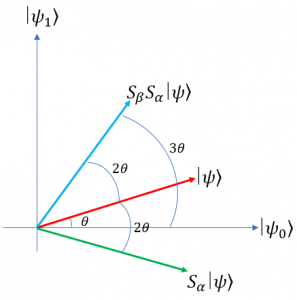
 (赤いベクトル)を軸
(赤いベクトル)を軸 に関して反転し、
に関して反転し、 (緑のベクトル)を作る。
(緑のベクトル)を作る。 (緑のベクトル)を軸
(緑のベクトル)を軸 に関して反転し、
に関して反転し、 (青いベクトル)を作る。
(青いベクトル)を作る。
この手順を経ると![]() は
は![]() に増えるので振幅も
に増えるので振幅も![]() に増えることになる。具体的に、演算
に増えることになる。具体的に、演算![]() の中身を見ていく。
の中身を見ていく。
![]() の導出:軸
の導出:軸![]() に関する反転なので、
に関する反転なので、![]() の
の![]() 軸成分が反転すればよい。したがって
軸成分が反転すればよい。したがって
(12) ![]()
が成り立てばよい。すなわち
(13) ![]()
である。
(14) ![]()
(15) ![]()
と一般化できる(上式において![]() とおけば式(14)を得る)。いま
とおけば式(14)を得る)。いま
(16) 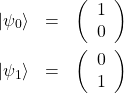
としたから
(17) ![]()
となる。天下り的であるが、求めるべき行列![]() は次式となる。
は次式となる。
(18) 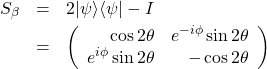
![]() は
は![]() の単位行列、
の単位行列、![]() は列ベクトルと行ベクトルの積なので行列である。
は列ベクトルと行ベクトルの積なので行列である。
以上で![]() が求まったので青色のベクトルは
が求まったので青色のベクトルは
(19) 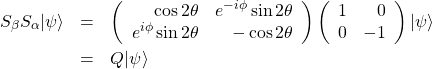
となる。ここで
(20) ![]()
である。ここまでの手順を繰り返すことによりさらに振幅を増幅させる。![]() 回繰り返した結果は
回繰り返した結果は
(21) ![]()
となる(計算は面倒ですが線形代数の基本問題です)。増幅前の状態は
(22) ![]()
であったから、![]() の成分が
の成分が![]() から
から![]() に増幅されたことが分かる。以上が量子振幅増幅のアルゴリズムである。
に増幅されたことが分かる。以上が量子振幅増幅のアルゴリズムである。
グローバーのアルゴリズム
上で説明した量子振幅増幅を使い、グローバーのアルゴリズムを説明する。考える問題は以下である。
(23)
ここで、
である。式(23)の右辺は、
桁の2進数
から
までの状態の重ね合わせである。ある関数
が定義されており、
を満たす
がただ1つ存在する。ほかの
については
である。状態
を見つけよ。
式(23)の右辺を変形すると
(24) ![]()
(25) 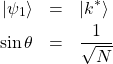
である。![]() が
が![]() になるまで増幅を行えば、式(24)の右辺の第1項の振幅は0(=
になるまで増幅を行えば、式(24)の右辺の第1項の振幅は0(=![]() )、第2項の振幅は1(=
)、第2項の振幅は1(=![]() )になる。増幅回数
)になる。増幅回数![]() は以下のように見積もることができる。式(21)より
は以下のように見積もることができる。式(21)より
(26) ![]()
したがって
(27) ![]()
となる。いまビット数![]() が十分大きいとき、
が十分大きいとき、![]() も十分大きくなる。このとき、式(25)の2つ目の式より
も十分大きくなる。このとき、式(25)の2つ目の式より![]() は十分小さくなり、
は十分小さくなり、![]() としてよい。したがって、
としてよい。したがって、![]() と置けるから、
と置けるから、![]() となる。すなわち、
となる。すなわち、![]() の手間で検索を行うことができる。以上がグローバーのアルゴリズムの内容である。
の手間で検索を行うことができる。以上がグローバーのアルゴリズムの内容である。
まとめ
今回は量子振幅増幅と呼ばれる手法を解説し、その応用例としてグローバーのアルゴリズムを紹介した。グローバーのアルゴリズムは、ソートされていないデータベースから特定のデータを探索する手法であり、![]() 個のデータに対し
個のデータに対し![]() 回の問い合わせで目的とするデータを発見できる。古典コンピュータの場合、問い合わせ回数は
回の問い合わせで目的とするデータを発見できる。古典コンピュータの場合、問い合わせ回数は![]() であるから、量子コンピュータを用いることで検索速度を加速させることができる。
であるから、量子コンピュータを用いることで検索速度を加速させることができる。
グローバーのアルゴリズムは、誤り耐性あり量子コンピュータ(FTQC)向けのアルゴリズムである。FTQCの実用化にはまだ多くの時間が必要であり、このアルゴリズムがすぐに実用化されることはないことを付記しておく。