はじめに
今回は量子位相推定と呼ばれる手法を解説する。量子フーリエ変換とともに、多くの量子アルゴリズム(暗号解読、量子化学、量子機械学習など)の要素技術として使われる手法である。
量子位相推定とは(概論)
量子アルゴリズムとは、さまざまな量子回路を組み合わせて構築するものであることを過去のブログで見てきた。量子回路は量子ゲートから構成され、1量子ゲートと2量子ゲートがあることも見た。1量子ゲートは、1量子ビットからなる状態ベクトル![]() (2次元列ベクトル)に
(2次元列ベクトル)に![]() のユニタリー行列
のユニタリー行列![]() (量子アルゴリズムで使われる演算は全てユニタリー性を持たなければならない)を施すものである。
(量子アルゴリズムで使われる演算は全てユニタリー性を持たなければならない)を施すものである。
(1) ![]()
図で示すと以下のようになる。左側が入力ビット、右側が出力ビットである。
![]()
![]() の固有値は一般に
の固有値は一般に![]() (
(![]() は
は![]() を満たす実数)と書くことができるので、対応する固有状態を
を満たす実数)と書くことができるので、対応する固有状態を![]() とすると
とすると
(2) ![]()
が成り立つ。固有状態![]() が既知のとき、位相
が既知のとき、位相![]() を求めるアルゴリズムが量子位相推定である。
を求めるアルゴリズムが量子位相推定である。
量子位相推定とは(詳細)
先のブログで量子フーリエ変換![]() を解説した。
を解説した。
(3) 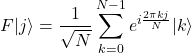
ここで、![]() であり、
であり、![]() は量子ビット数である。式(3)を眺めると、左辺の状態ベクトル内にある
は量子ビット数である。式(3)を眺めると、左辺の状態ベクトル内にある![]() が右辺の指数関数の肩に移動していることが分かる。つまり、逆フーリエ変換をすれば、指数関数の肩にある値を状態ベクトル内部に移すことができる。
が右辺の指数関数の肩に移動していることが分かる。つまり、逆フーリエ変換をすれば、指数関数の肩にある値を状態ベクトル内部に移すことができる。
(4) 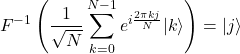
この事実を踏まえて式(2)を見直す。いま求めたい値![]() は指数関数の肩に乗っているので、逆フーリエ変換を利用して状態ベクトル側に下ろす。その後この状態を測定することにより
は指数関数の肩に乗っているので、逆フーリエ変換を利用して状態ベクトル側に下ろす。その後この状態を測定することにより![]() の値を知ることできるだろう。この方針に従って以下の計算を行う。
の値を知ることできるだろう。この方針に従って以下の計算を行う。
まず最初に、![]() 個の量子ビットを用意する。これらをまとめて第1レジスタと呼ぶことにする(下図参照)。全ての量子ビットの状態を0に初期化する。第1レジスタとは別に
個の量子ビットを用意する。これらをまとめて第1レジスタと呼ぶことにする(下図参照)。全ての量子ビットの状態を0に初期化する。第1レジスタとは別に![]() 個の量子ビットから成る第2レジスタを用意する。第2レジスタ上には固有値を求めたいユニタリー行列
個の量子ビットから成る第2レジスタを用意する。第2レジスタ上には固有値を求めたいユニタリー行列![]() の固有状態
の固有状態![]() が既に実現されているとする。
が既に実現されているとする。

第1レジスタと第2レジスタを合わせた全状態を![]() と書くことにすると
と書くことにすると
(5) ![]()
となる。ここで、![]() は同じ状態を
は同じ状態を![]() 回繰り返すことを意味する(
回繰り返すことを意味する(![]() 個の直積)。次に、第1レジスタに属する個々の量子ビットに
個の直積)。次に、第1レジスタに属する個々の量子ビットに![]() ゲート(アダマールゲート)を作用させる(下図参照)。
ゲート(アダマールゲート)を作用させる(下図参照)。

(6) 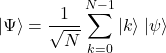
ここで、![]() とした。式(6)の第1レジスタの状態がどのような状態なのかを、
とした。式(6)の第1レジスタの状態がどのような状態なのかを、![]() の場合に調べてみる。
の場合に調べてみる。
(7) 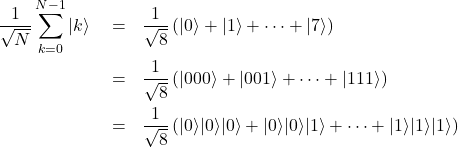
式中の左から右への量子ビットの並び![]() は、図における量子ビットの上から下への並びに対応している(下図参照)。
は、図における量子ビットの上から下への並びに対応している(下図参照)。
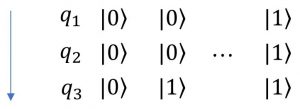
以上が3量子ビットのときの第1レジスタの内容である。この後の説明を一般の![]() 量子ビットに戻って行うと分かり難くなるので、もうしばらく3量子ビットのまま説明を続ける。
量子ビットに戻って行うと分かり難くなるので、もうしばらく3量子ビットのまま説明を続ける。
アダマールゲートの後、第1レジスタの各ビットを制御ビットとして第2レジスタに![]() の累乗を作用させる(下図参照)。
の累乗を作用させる(下図参照)。
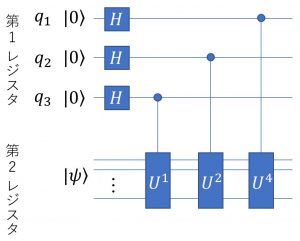
制御ビットが1の時のみ![]() を作用させると言う意味である。全状態は以下のようになる。
を作用させると言う意味である。全状態は以下のようになる。
(8) ![]()
例えば、式(8)の右辺第2項を見てみる。第1レジスタの![]() ビットは1であるから上の回路図より第2レジスタに
ビットは1であるから上の回路図より第2レジスタに![]() がかかる。また、第4項は
がかかる。また、第4項は![]() ビットと
ビットと![]() ビットが1である。上の回路図を見ると、
ビットが1である。上の回路図を見ると、![]() ビットと紐づいている演算は
ビットと紐づいている演算は![]() 、
、![]() ビットと紐づいている演算は
ビットと紐づいている演算は![]() であるからトータルで
であるからトータルで![]() が第2レジスタに作用する。ここまでの考察で、第1レジスタの2進数を10進数に変換した値が
が第2レジスタに作用する。ここまでの考察で、第1レジスタの2進数を10進数に変換した値が![]() の肩に乗ることが分かったので
の肩に乗ることが分かったので
(9) 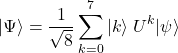
とまとめることができる。ここまでくれば一般の![]() ビットの場合に拡張するのは容易である。
ビットの場合に拡張するのは容易である。
(10) 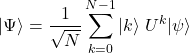
(11) ![]()
が成り立つのでこれを代入すると
(12) 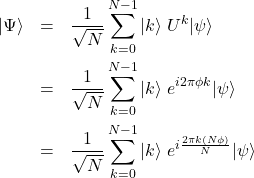
を得る。式(4)の逆フーリエ変換は以下であった。
(13) 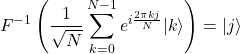
この式に出てくる![]() を
を![]() と思えば、第1レジスタに逆フーリエ変換をかけた後の状態は次式となる。
と思えば、第1レジスタに逆フーリエ変換をかけた後の状態は次式となる。
(14) ![]()
このときの量子回路は下図である(3量子ビットのとき)。
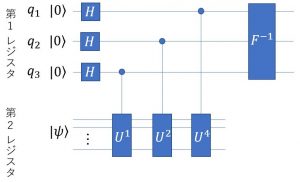
最後に第1レジスタを測定し![]() で割れば
で割れば![]() を求めることができる。
を求めることができる。
上の計算は![]() が整数となる場合に成り立つ結果である。
が整数となる場合に成り立つ結果である。![]() が整数とならない場合でも、その値に近い状態が高い確率で観測される。その誤差は
が整数とならない場合でも、その値に近い状態が高い確率で観測される。その誤差は![]() を
を![]() で割った程度であるから、ビット数
で割った程度であるから、ビット数![]() を増やすほど精度は良くなる。
を増やすほど精度は良くなる。
実装
ここまでのロジックを、IBMのSDKQiskitを用いて実装してみる(ソースコードはここにある。)。![]() として次を考える。
として次を考える。
(15) ![]()
ここで
(16) ![]()
であることを思い出せば、次式が成り立つことが分かる。
(17) ![]()
つまり、![]() の固有値は
の固有値は![]() 、固有状態
、固有状態![]() は
は![]() である。式(11)と対応させれば、
である。式(11)と対応させれば、![]() である。量子回路を作るコードは以下のようになる。
である。量子回路を作るコードは以下のようになる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
import math import qiskit # 第2レジスタのビット数 N_EIGEN_STATE = 1 def execute_IQFT_core(circuit, target, n): for control in range(0, target): circuit.cp(-math.pi / 2 ** (target - control), control, target) circuit.h(target) def execute_IQFT(circuit, n): """ 逆フーリエ変換(IQFT)を実行 """ # ビットの並びを反転 for i in range(math.floor(n / 2)): circuit.swap(i, n - (i + 1)) for i in range(n): execute_IQFT_core(circuit, i, n) def make_circuit(n_encode: int): """ 量子位相推定を実行する。 Parameters ----- n_encode: int 第2レジスタのビット数 Returns ----- qc: qiskit.QuantumCircuit 作成した回路 theta: qiskit.circuit.Parameter 後で設定する位相 """ n = n_encode + N_EIGEN_STATE qc = qiskit.QuantumCircuit(qiskit.QuantumRegister(n), qiskit.ClassicalRegister(n_encode)) # 第2レジスタをUの固有状態にする。 qc.x(n_encode) # 第1レジスターのそれぞれのビットにアダマールゲートを作用させる。 for qubit in range(n_encode): qc.h(qubit) # 第1レジスターの各ビットを制御ビットにして第2レジスタにユニタリー操作をおこなる。 theta = qiskit.circuit.Parameter('φ') r = 1 for c in range(n_encode): for i in range(r): qc.cp(theta, control_qubit=c, target_qubit=n_encode) r *= 2 qc.barrier() # 逆フーリエ変換 execute_IQFT(qc, n_encode) qc.barrier() # 第1レジスタの各ビットを測定する。 for n in range(n_encode): # n番目の量子ビットを測定してn番目の古典ビットに保存する。 qc.measure(n, n) return qc, theta |
この回路を実行するコードは以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
import quantum_phase_estimation as QPE from qiskit.visualization import plot_histogram import matplotlib.pyplot as plt import numpy as np import qiskit # 第1レジスタのビット数 N_ENCODE = 5 if __name__ == "__main__": # 回路を作る。 qc, theta = QPE.make_circuit(N_ENCODE) # θ=2*pi*φを与える(正解値) phase = np.random.rand() # 回路にパラメータを設定する。 qc_parametrized = qc.bind_parameters({theta: phase}) # シミュレータを選択する。 backend = qiskit.Aer.get_backend('qasm_simulator') # 実行回数 shots = 1024 # 計算する。 results = qiskit.execute(qc_parametrized, backend=backend, shots=shots).result() # 結果をとりだす。 answer = results.get_counts() # 測定された位相を算出する。 values = list(results.get_counts().values()) keys = list(results.get_counts().keys()) idx = np.argmax(list(results.get_counts().values())) ans = int(keys[idx], 2) phase_estimated = ans / (2 ** N_ENCODE) # 正しい位相の値 true_phase = phase / (2 * np.pi) print('True phase: {:.4f}'.format(true_phase)) print('Estimated phase: {:.4f}'.format(phase_estimated)) print('Diff: {:.4f}'.format(np.abs(true_phase - phase_estimated))) # ヒストグラムを描画して保存する。 plot_histogram(answer, figsize=(20, 7)) plt.savefig("./histogram.jpg") |
8行目のN_ENCODEは第1レジスタのビット数である。16行目で![]() の正解値を与える。今回は量子コンピュータの実機ではなくPC上で行うシミュレーターを選択した(22行目)。28行目で計算を実行し、38行目で位相
の正解値を与える。今回は量子コンピュータの実機ではなくPC上で行うシミュレーターを選択した(22行目)。28行目で計算を実行し、38行目で位相![]() の推定結果を算出する。45行目で正解値との差分を計算している。実際に計算したときの出力は以下のようになる。
の推定結果を算出する。45行目で正解値との差分を計算している。実際に計算したときの出力は以下のようになる。
|
1 2 3 |
True phase: 0.1178 Estimated phase: 0.1250 Diff: 0.0072 |
第1レジスタの様子は以下のようになる。
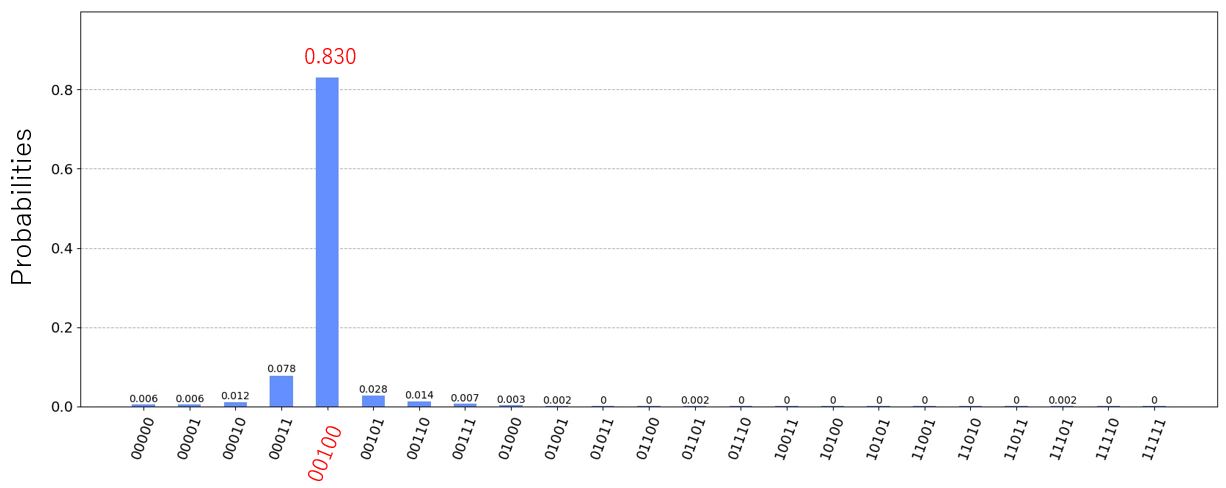
量子ビット数を5としたから横軸の最大値は11111(10進数で31(=![]() ))である。縦軸は各ビットの実現確率を表す。このヒストグラムを見ると、状態4(=00100)の実現確率が最も高いことが分かる。従って推定された位相
))である。縦軸は各ビットの実現確率を表す。このヒストグラムを見ると、状態4(=00100)の実現確率が最も高いことが分かる。従って推定された位相![]() の値は
の値は![]() となる。正解値とのずれは0.0072である。
となる。正解値とのずれは0.0072である。
まとめ
今回は、量子位相推定(QPE)のアルゴリズを解説した。さまざまな分野(量子化学・暗号読解など)での応用が考えられる要素技術である。しかし、QPEを精度よく実行するには、現在の小規模な量子コンピュータ(NISQ)では無理であり、誤り訂正のある大規模な量子コンピュータ(FTQC)の出現を待つ必要がある。その時期は2029年ごろと言われている(記事)。

