はじめに
最近、量子コンピュータの話題が多くなっている。理論やハードウェアの進歩に伴い、商業化や収益化を視野に入れた動きも出てきた。今回は、先の記事の続きとして「量子もつれ」について解説する。量子もつれは、量子コンピュータに高速さをもたらし、現実世界ではあり得ないような振る舞いを示す現象である。
1量子ビット
先の記事では、量子ビットが1つの状態として
(1) ![]()
を考えた。ここで、![]() は列ベクトルを表し、量子力学ではケットベクトルと呼ばれる量である。
は列ベクトルを表し、量子力学ではケットベクトルと呼ばれる量である。![]() と
と![]() は
は
(2) 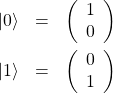
で定義される。また![]() と
と![]() は確率振幅と呼ばれる量であり複素数である。量子力学では、確率振幅の絶対値の2乗が確率を表すので、式(1)は次のように解釈される。すなわち、状態
は確率振幅と呼ばれる量であり複素数である。量子力学では、確率振幅の絶対値の2乗が確率を表すので、式(1)は次のように解釈される。すなわち、状態![]() が
が![]() である確率が
である確率が![]() 、
、![]() である確率が
である確率が![]() である。確率であるから次式が成り立つ。
である。確率であるから次式が成り立つ。
(3) ![]()
これは、状態![]() の規格化条件である。
の規格化条件である。
2量子ビット
(4) ![]()
(5) ![]()
となる。ここで記号![]() はテンソル積(直積)と呼ばれる量であり、左のビットと右のビットが独立してそれぞれの状態を取れることを意味する。この右辺を、普通の文字式同士の掛け算とみなして展開すると
はテンソル積(直積)と呼ばれる量であり、左のビットと右のビットが独立してそれぞれの状態を取れることを意味する。この右辺を、普通の文字式同士の掛け算とみなして展開すると
(6) ![]()
となる。ただし、簡単のため、![]() を
を![]() と書いた。上式の右辺より、2量子ビットの状態は、4つの状態
と書いた。上式の右辺より、2量子ビットの状態は、4つの状態![]() の線形結合で表されることが分かる。
の線形結合で表されることが分かる。![]() と書き直すと
と書き直すと
(7) ![]()
となる。1量子ビットのときの規格化条件(3)に相当するのが次式である。
(8) ![]()
状態![]() が、
が、![]() となる確率が
となる確率が![]() 、
、![]() となる確率が
となる確率が![]() 、
、![]() となる確率が
となる確率が![]() 、
、![]() となる確率が
となる確率が![]() である。
である。![]() は条件(8)を満たす複素数であればどのような数でも良い。
は条件(8)を満たす複素数であればどのような数でも良い。
量子もつれ
![]() のとき、式(6)から(5)へ遡ることができるので、2量子ビット状態は左側のビット
のとき、式(6)から(5)へ遡ることができるので、2量子ビット状態は左側のビット![]() と右側のビット
と右側のビット![]() に分離できる。このことをもっと一般的な条件で言い換えると、
に分離できる。このことをもっと一般的な条件で言い換えると、![]() が成り立つとき、2量子ビット状態は左側のビット
が成り立つとき、2量子ビット状態は左側のビット![]() と右側のビット
と右側のビット![]() に分離できる。ところで、
に分離できる。ところで、![]() は条件(8)を満たす複素数であればどのような数でも良いので、
は条件(8)を満たす複素数であればどのような数でも良いので、![]() となる
となる![]() も存在する。このとき2量子ビット状態は左右のビットに分離できない。このような状態を「量子もつれ状態」と呼ぶ。例えば次の状態は量子もつれ状態である。
も存在する。このとき2量子ビット状態は左右のビットに分離できない。このような状態を「量子もつれ状態」と呼ぶ。例えば次の状態は量子もつれ状態である。
(9) ![]()
(10) ![]()
測定
量子コンピュータと古典的なコンピュータの間の大きな違いの1つに、測定が系に与える影響を挙げることできる。従来のコンピュータの計算結果が、計算を行う回路内の電圧や電流などの測定から影響を受けることはない。一方、量子コンピュータにおける測定は、結果に対して本質的な影響を与える。従って、量子ビットを処理する回路(量子回路と呼ぶ)には、測定という行為も1つのファクタとして組み込まれている。
次の1量子ビット状態を考え、測定についての量子力学の約束事をまとめる。
(11) ![]()
- 測定を行う前は、状態
 は
は  なのか
なのか  なのかはわからない。
なのかはわからない。 - 測定を行うと、状態
 は
は  か
か  のいずれかになる。
のいずれかになる。  が測定される確率は
が測定される確率は  、
、 が測定される確率は
が測定される確率は  である。
である。 が測定されれば状態は
が測定されれば状態は に、
に、 が測定されれば状態は
が測定されれば状態は に「収縮」する。
に「収縮」する。
もつれた状態の測定
さて、もつれた状態(式(10))
(12) ![]()
を測定してみる。最初に左側のビットを測定する。式(12)の右辺第1項の左側ビットは![]() 、第2項の左側ビットは
、第2項の左側ビットは![]() であり、これらの係数はどちらも
であり、これらの係数はどちらも![]() であるから確率は1/2である。
であるから確率は1/2である。![]() が得られるか
が得られるか![]() が得られるかは半々の確率である。いま、
が得られるかは半々の確率である。いま、![]() が得られたとする。このとき、右側ビットはどうなるか。左側ビットが
が得られたとする。このとき、右側ビットはどうなるか。左側ビットが![]() に確定した瞬間に状態
に確定した瞬間に状態![]() は以下の状態に収縮する。
は以下の状態に収縮する。
(13) ![]()
すなわち、右側ビットは![]() に確定してしまう。最初の測定で左側ビットが
に確定してしまう。最初の測定で左側ビットが![]() と測定されるなら、右側ビットは100%の確率で
と測定されるなら、右側ビットは100%の確率で![]() になると言い切ることができる。つまり、こう言うことである。
になると言い切ることができる。つまり、こう言うことである。
2量子ビットがどのような状態にあるかは測定するまで分からない。もし、2量子ビット状態がもつれた状態にあるなら、片方のビットの測定がもう片方の状態を決めてしまう。
ここまでの考察で2つの量子ビットの間の空間的な距離は考えてこなかった。実は量子もつれという現象は、2つのビットがどれだけ離れていようと成り立つことが実験的に確認されている。2017年に中国の研究チームが地上と軌道上にいる衛星との間で量子もつれを観測したと報告している。測定前は状態は分からないが、地上(衛星)で片方のビットを測定すると、もう片方のビットの状態は瞬時に確定するのである。ただし、地上(衛星)での測定結果を衛星(地上)に伝える必要があり、その速度は光速を超えないので、光速を超えて情報が伝達するわけではない。量子もつれがどのような仕組みで起きるのかを説明する理論は存在しないが、この状況を完全に記述する理論は存在する。それが量子力学である。
量子もつれのシミュレーション
量子ビットにさまざまな処理を施す回路の部品を量子ゲートと呼ぶ。量子ゲートをPC(古典コンピュータ)上でシミュレートするPythonフレームワークのひとつにBlueqatがある。これを用いて、量子もつれ状態を作成してみる。最初に、量子もつれ状態を作るために必要な2つの量子ゲート、CNOTゲートとアダマールゲートを紹介する。
アダマールゲート
アダマール(Hadamard)ゲートの回路図は以下の通りである。

上図において![]() はそれぞれ1量子ビット状態を表す。aが入力ビット、bが出力ビットである。アダマールゲートは以下のように状態を変換する。
はそれぞれ1量子ビット状態を表す。aが入力ビット、bが出力ビットである。アダマールゲートは以下のように状態を変換する。
(14) 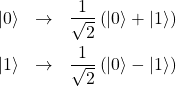
矢印の左側が![]() を、右側が
を、右側が![]() を表す。
を表す。
CNOTゲート
CNOTゲートの回路図は以下の通りである。
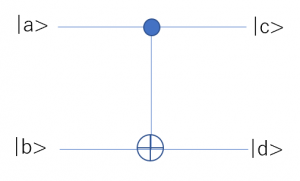
上図において![]() はそれぞれ1量子ビット状態を表す。左側の2つが入力であり、右側の2つが出力である。ビットaを制御ビットと呼び、塗りつぶされた円はaが制御ビットであることを表す。また、ビットbにつながる線上にある十字の丸は古典回路でも使われる排他的論理和である。CNOTゲートでは、a=1のときのみbのビットが反転する。例えば、
はそれぞれ1量子ビット状態を表す。左側の2つが入力であり、右側の2つが出力である。ビットaを制御ビットと呼び、塗りつぶされた円はaが制御ビットであることを表す。また、ビットbにつながる線上にある十字の丸は古典回路でも使われる排他的論理和である。CNOTゲートでは、a=1のときのみbのビットが反転する。例えば、![]() のとき
のとき![]() となり、
となり、![]() のとき
のとき![]() となる。aの状態はそのまま保持されcに出力されることに注意する。ここで、2つの状態
となる。aの状態はそのまま保持されcに出力されることに注意する。ここで、2つの状態
(15) 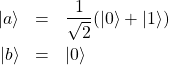
を考える。これはテンソル積を用いて
(16) 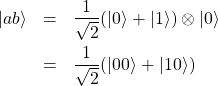
と書くことができる。これはCNOTゲートにより
(17) ![]()
となる。上式は先に見たように2つの量子状態![]() ,
,![]() が量子もつれ状態にあることを表す。従って、2つの状態のテンソル積の形(
が量子もつれ状態にあることを表す。従って、2つの状態のテンソル積の形(![]() )で書くことができない。
)で書くことができない。
量子もつれを作る回路
さて、アダマールゲートとCNOTゲートを組み合わせた次の回路を使うと量子もつれを作ることができる。
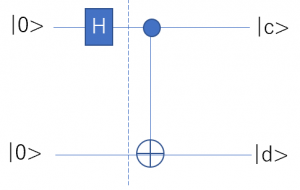
入力は![]() である。ビットaにアダマールゲートを作用させた後の状態(図の破線部分)は
である。ビットaにアダマールゲートを作用させた後の状態(図の破線部分)は
(18) ![]()
である。この状態にCNOTゲートを作用させた後の状態は上のCNOTゲートの説明で見たように量子もつれ状態になる。
(19) ![]()
つまり、上の回路により入力![]() が出力
が出力![]() に変換された。
に変換された。
Blueqatを用いたシミュレーション
道具が揃ったので、Blueqatを用いて、PC上でシミュレートしてみる。コードは以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import blueqat as bq if __name__ == "__main__": # 2量子ビットを使う回路 c = bq.Circuit(2) # アダマールゲートを最初のビット0に適用 x = c.h[0] # ビット0を制御ビットにしてビット1にNOTゲートを適用 x = x.cx[0, 1] # 1000回測定する。 y = x.m[:].run(shots=1000) print(y) |
出力は以下の通り。
|
1 |
Counter({'11': 522, '00': 478}) |
状態![]() が522回、状態
が522回、状態![]() が478回測定されたことを表している。ほぼ半々である。量子力学の結果は確率で与えられることをもう一度強調しておく。
が478回測定されたことを表している。ほぼ半々である。量子力学の結果は確率で与えられることをもう一度強調しておく。
まとめ
今回は量子もつれの説明を行い、PythonフレームワークBlueqatを用いて、シミュレートしてみた。量子コンピュータを使うアルゴリズムの実装は、様々な量子ゲート(今回は2つだけ紹介した)を組み合わせて上記のように記述していく作業になる。既存の機械学習のアルゴリズムを量子回路で書き直す作業についてもいずれ紹介したい。

