はじめに
量子テレポーテーションという単語をGoogleで検索すると、量子テレポーテーションの実験に成功した主旨の記事がたくさん見つかる。今回は、この量子テレポーテーションを解説する。量子テレポーテーションにはいくつかの基本的な量子ゲートが使われている。本記事では、これらの基本要素を説明したあと、量子テレポーテーションについて解説する。
量子テレポーテーションとは
2つの量子ビット(量子ビットについては過去記事を参照)を考え、それらを何らかの手法で量子もつれ状態にする(量子もつれについても過去記事を参照)。量子もつれ状態が壊れないように注意を払いつつ、2つの量子ビットの一方をアリスに、もう一方をボブの手元に置く(下図参照)。アリスの手元にはもう1つの量子ビットを置く。アリスの2つの量子ビットはそのままアリスの手元にあり続け、ボブの1つの量子ビットもボブの手元にあり続ける。3つの量子ビットに下図のように「量子ビット1」「量子ビット2」「量子ビット3」と名前を付ける。
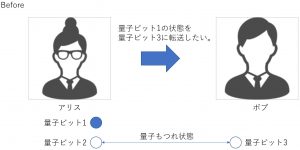
このような状態にあるとき、ある一連の操作(後述)をすることで、アリスの手元にある量子ビット1の状態を、ボブの手元にある量子ビット3に転送(再現)することができる(下図)。
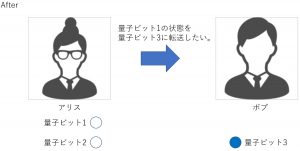
この一連の操作(詳細は後述する)を量子テレポーテーションと呼ぶ。アリスとボブの間の物理的な距離は、転送前の量子もつれ状態が維持できるのであれば、いくらでも長くとることができる。例えば、中国の研究チームは2017年に地上と通信衛星との間で量子テレポーテーションを成功させている(論文)。
量子テレポーテーションを実現するのに必要な量子ゲートについて最初に説明する。過去のブログで説明したとおり、1量子ビットは2つの状態![]() と
と![]() を持つ。それぞれは2次元の列ベクトルで表現される。
を持つ。それぞれは2次元の列ベクトルで表現される。
(1) 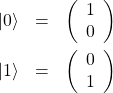
以下で説明する各種ゲートはこのベクトルに作用する行列(ユニタリ行列)である。
 ゲート、
ゲート、 ゲート、
ゲート、 ゲート、
ゲート、 ゲート
ゲート
![]() ゲートは次式を満たす。
ゲートは次式を満たす。
(2) ![]()
行列表記は以下となる。
(3) ![]()
また、以下のように図示される。

![]() ゲートは、ビットを反転させる量子ゲートである。
ゲートは、ビットを反転させる量子ゲートである。
![]() ゲートは次式を満たす。
ゲートは次式を満たす。
(4) ![]()
つまり、![]() の符号(位相)を反転させるゲートである。行列表記は以下となる。
の符号(位相)を反転させるゲートである。行列表記は以下となる。
(5) ![]()
以下のように図示される。

![]() ゲートは次式を満たす。
ゲートは次式を満たす。
(6) 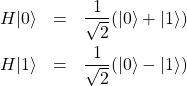
行列表記は以下となる。
(7) ![]()
以下のように図示される。
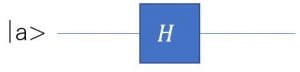
これはHadamarl(アダマール)ゲートと呼ばれる。先のブログでも解説したように、係数の2乗がその状態が実現する確率を表す。アダマールゲートを作用させた後の状態は、![]() が実現する確率は1/2、
が実現する確率は1/2、![]() が実現する確率も1/2である。
が実現する確率も1/2である。
最後に、![]() ゲートを以下に示す。これは2量子ビットに作用するゲートである。
ゲートを以下に示す。これは2量子ビットに作用するゲートである。
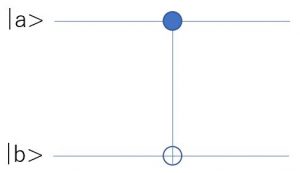
量子ビットaが1のときだけ量子ビットbを反転させ、量子ビットaが0のときは何もしない。
量子テレポーテーション
材料が揃ったので量子テレポーテーションについて説明する。最初にアリスとボブの手元に置く材料を以下に示す。
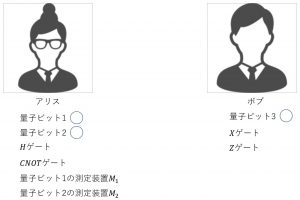
アリスの手元には
があり、ボブの手元には
がある。量子テレポーテーションを実現する量子回路は下図である。
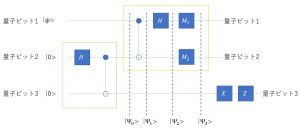
量子ビット1と2はアリスの手元に、量子ビット3はボブの手元にある。アリスが持つ量子ビット1の状態をボブの持つ量子ビット3に転送することが目的である。
最初に、アリスとボブは同じ場所におり、緑の枠で囲った量子回路を用いて、それぞれが持つ量子ビット2と3を量子もつれ状態にする。
(8) ![]()
これは次式を簡略化した書き方である。
(9) ![]()
量子もつれが実現できたら、この状態を維持したまま二人は離れ、そのあとの作業は別々の場所で行う。まず最初に、オレンジ色の枠で囲ったアリスが行う作業を説明する。図中の状態![]() は
は
(10) ![]()
である。いま、量子ビット1の状態![]() を
を
(11) ![]()
と書くことにすると、量子ビット1と2にCNOTゲートを作用させた後の状態![]() は
は
(12) ![]()
となる。量子ビット1にアダマールゲートを作用させた後の状態![]() は
は
(13) 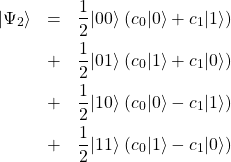
となる。右辺4項の全ての係数が1/2であるから、各項が実現する確率は全て1/4である(係数の2乗が確率になるのであった)。このタイミングでアリスは量子ビット1と2の状態を測定器![]() と
と![]() を用いて測定する。量子ビット1と2の状態が(0,0)ならボブの持つ量子ビット3の状態は
を用いて測定する。量子ビット1と2の状態が(0,0)ならボブの持つ量子ビット3の状態は![]() に確定する。つまり、量子ビット1,2は(0,0)に、量子ビット3の状態が
に確定する。つまり、量子ビット1,2は(0,0)に、量子ビット3の状態が![]() に決まるので全量子ビットの状態
に決まるので全量子ビットの状態![]() は
は
(14) ![]()
になる。量子ビット1と2の状態は測定されたので上の表式からは除いた。量子ビット3の状態はまだ測定されていないので0なのか1なのかは不明なままであることに注意する。同様に、量子ビット1,2が(0,1)なら
(15) ![]()
量子ビット1,2が(1,0)なら
(16) ![]()
量子ビット1,2が(1,1)なら
(17) ![]()
になる。アリスの測定により、離れた場所にいるボブの量子状態は上の4つのいずれかに確定する。ここで、アリスからボブにアリス側の測定結果を伝える。テキスト情報を郵便で送ってもいいし、メールで知らせても良い。その結果ボブは自分が持つ量子ビット3の状態を確定することができる。アリスから受け取った情報が(0,0)ならボブの状態は
(18) ![]()
である。これは最初の量子ビット1が持っていた状態![]() であるから、目的は達成できた。アリスから受け取った情報が(0,1)ならボブの状態は
であるから、目的は達成できた。アリスから受け取った情報が(0,1)ならボブの状態は
(19) ![]()
である。(0,1)を受け取ったボブは量子ビット3に![]() ゲートを作用させれば
ゲートを作用させれば![]() を得ることができる。アリスから受け取った情報が(1,0)ならボブの状態は
を得ることができる。アリスから受け取った情報が(1,0)ならボブの状態は
(20) ![]()
である。(1,0)を受け取ったボブは量子ビット3に![]() ゲートを作用させれば
ゲートを作用させれば![]() を得ることができる。アリスから受け取った情報が(1,1)ならボブの状態は
を得ることができる。アリスから受け取った情報が(1,1)ならボブの状態は
(21) ![]()
である。(1,1)を受け取ったボブは量子ビット3に![]() ゲートを作用させ、そのあと
ゲートを作用させ、そのあと![]() ゲートを作用させれば
ゲートを作用させれば![]() を得ることができる。以上のように、アリスから受け取る情報に応じてボブ側の作業を変えることにより、アリスが持っていた量子ビット1の状態を、離れた場所にいるボブの手元にある量子ビット3へ転送できる。これが量子テレポーテーションである。
を得ることができる。以上のように、アリスから受け取る情報に応じてボブ側の作業を変えることにより、アリスが持っていた量子ビット1の状態を、離れた場所にいるボブの手元にある量子ビット3へ転送できる。これが量子テレポーテーションである。
補足
詳細は省くが、「量子ビットは複製できない」という重要な定理がある(non-cloning theorem:量子複製不可能定理)。アリスの手元で実現していた量子ビット1の状態は、ボブに転送したあと壊れる。
まとめ
今回は、量子テレポーテーションについて説明した。これは机上の理論ではなく実際に実験でも確認されている現象である。上の例で一点注意しなければならないことがある。アリスからボブに測定結果を伝えるには従来の通信手段を使う必要があるということである。従って一瞬で情報が伝わるわけではない。もしそうであれば物理法則が破綻してしまう。
量子テレポーテーションで使われる量子もつれという現象は不思議な現象である。その振る舞いは量子力学で記述できるが、その仕組みは分かっていない。最近読んだ本で、有名な理論物理学者が量子もつれとワームホールの関係に言及していることを知った。ググってみると日経新聞に関連記事が見つかった。ワームホールとは「時空のある一点から別の離れた一点へと直結する空間領域でトンネルのような抜け道である」(by Wikipedia)。宇宙戦艦ヤマトに出てきた「ワープ」である。本当かしら。

