はじめに
今回は、時系列解析の3回目として以下を紹介する。
- ARMA過程
- ARIMA過程
- SARIMA過程
MA過程とAR過程
最初に、先の2回で紹介したMA過程とAR過程の長所と短所をまとめておく。

図1
ARMA過程
ARMA(![]() )過程とは、先の2回で説明した2つの過程、AR(
)過程とは、先の2回で説明した2つの過程、AR(![]() )過程とMA(
)過程とMA(![]() )過程を組み合わせたものである。AR(
)過程を組み合わせたものである。AR(![]() )過程は次式で定義された。
)過程は次式で定義された。
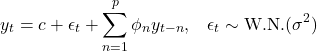
ここで、W.N.(![]() )は分散
)は分散![]() を持つホワイト・ノイズ、
を持つホワイト・ノイズ、![]() は定数である。AR(
は定数である。AR(![]() )過程は
)過程は![]() 個の過去データの線形和で現時刻の値
個の過去データの線形和で現時刻の値![]() を表す。また、MA(
を表す。また、MA(![]() )過程は次式で与えられた。
)過程は次式で与えられた。
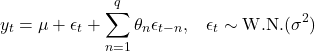
ここで、![]() は定数である。MA(
は定数である。MA(![]() )過程は
)過程は![]() 個のホワイト・ノイズの線形和で記述される。これらを組み合わせたARMA(
個のホワイト・ノイズの線形和で記述される。これらを組み合わせたARMA(![]() )過程は次式で定義される。
)過程は次式で定義される。
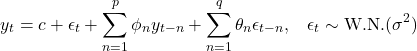
「時系列解析-1」で見たように、MA(![]() )過程は常に定常であった(定常とは、期待値
)過程は常に定常であった(定常とは、期待値![]() と自己共分散
と自己共分散![]() が時間に依存しない状態を表すのであった)。従って、ARMA(
が時間に依存しない状態を表すのであった)。従って、ARMA(![]() )が定常になるか否かは、ARMA(
)が定常になるか否かは、ARMA(![]() )過程の中のAR(
)過程の中のAR(![]() )過程の部分が定常になるか否かによって決まる。
)過程の部分が定常になるか否かによって決まる。
詳細な議論は省くが、ARMA(![]() )過程は定常過程を対象とする場合に高い説明能力を持つことが知られている。従って、このARMA(
)過程は定常過程を対象とする場合に高い説明能力を持つことが知られている。従って、このARMA(![]() )過程を用いて時系列解析を行う場合、まず最初に、与えられた時系列データを定常過程に変換する作業が行われる。具体的な変換方法を次に示す。
)過程を用いて時系列解析を行う場合、まず最初に、与えられた時系列データを定常過程に変換する作業が行われる。具体的な変換方法を次に示す。
非定常過程から定常過程へ
定常過程への変換方法は簡単である。差分を取れば良い。いま時系列データ![]() の1階差分系列を考える。
の1階差分系列を考える。
![]()
1階差分系列と区別するため元の系列![]() を原系列と呼ぶことにする。原系列が非定常過程であり1階差分系列が定常過程のとき、原系列
を原系列と呼ぶことにする。原系列が非定常過程であり1階差分系列が定常過程のとき、原系列![]() を単位根過程
を単位根過程![]() と呼ぶ。1階差分系列
と呼ぶ。1階差分系列![]() が非定常過程の場合には、さらに差分を考える。
が非定常過程の場合には、さらに差分を考える。
![]()
1階差分系列![]() が非定常過程であり2階差分系列
が非定常過程であり2階差分系列![]() が定常過程の時、原系列
が定常過程の時、原系列![]() を2次和分過程
を2次和分過程![]() と呼ぶ。一般に
と呼ぶ。一般に![]() 階差分系列が非定常過程であり
階差分系列が非定常過程であり![]() 階差分過程が定常過程のとき、原系列は
階差分過程が定常過程のとき、原系列は![]() 次和分過程
次和分過程![]() と呼ばれる。
と呼ばれる。
次に、差分を取ることにより非定常過程から定常過程に変化する仕組みを説明する。例として次の過程を考える。
![]()
ここで、![]() は定数である。これはランダム・ウォークと呼ばれる過程である。この過程は係数
は定数である。これはランダム・ウォークと呼ばれる過程である。この過程は係数![]() が1のAR(1)過程であるから非定常過程である(「時系列解析-2」を参照)。さて、この過程の1階差分過程を計算する。
が1のAR(1)過程であるから非定常過程である(「時系列解析-2」を参照)。さて、この過程の1階差分過程を計算する。
![]()
これはホワイトノイズ(プラス定数)であるから定常過程になる。今の場合は一度の差分で定常過程となったが、複数回の差分を繰り返すことにより定常過程になる場合もある。このように非定常過程は差分を取ることにより定常過程に変換できることが多い。与えられた過程に対し差分を取るべきか否かの判定は次のKPSS検定で行うことができる。
KPSS検定
差分前は非定常、差分後は定常になるか否かを判断する一手法としてKPSS検定がある。この検定では、原系列![]() として次式を仮定する。
として次式を仮定する。
(1) ![]()
ここで、![]() は定数である。
は定数である。![]() はトレンド項と呼ばれ、時系列データを単調に増加させるか減少させる。
はトレンド項と呼ばれ、時系列データを単調に増加させるか減少させる。![]() は
は
![]()
を満たすランダム・ウォークであり、![]() である。ここで、
である。ここで、![]() は、平均0、分散
は、平均0、分散![]() の独立同分布からのサンプリングを表す。
の独立同分布からのサンプリングを表す。![]() は定常過程を表す。いま2つの仮説を定義する。
は定常過程を表す。いま2つの仮説を定義する。
- 帰無仮説:
 (単位根なし。差分とらない)
(単位根なし。差分とらない) - 対立仮説:
 (単位根あり。差分をとる)
(単位根あり。差分をとる)
帰無仮説が成り立つ場合、![]() であるからランダム・ウォークは定常過程になることに注意する。この2つの仮説に対し検定を行うのがKPSS検定である。帰無仮説が成立する確率(危険率)が5%(一般的に使われる値)より低ければ帰無仮説を棄却する。つまり、単位根あり(差分をとるべき)と判断する。
であるからランダム・ウォークは定常過程になることに注意する。この2つの仮説に対し検定を行うのがKPSS検定である。帰無仮説が成立する確率(危険率)が5%(一般的に使われる値)より低ければ帰無仮説を棄却する。つまり、単位根あり(差分をとるべき)と判断する。
ARMAの派生モデル
以下、ARMAの派生モデルを紹介する。
ARIMAモデル
先にARMAモデルは定常過程に対し高い説明能力を持つと述べた。原系列の差分を取ることにより定常化した過程(![]() 次和分過程
次和分過程![]() )に対しARMAモデルを適用したモデルをARIMA(
)に対しARMAモデルを適用したモデルをARIMA(![]() )モデルと呼ぶ。この数式を書きおろすには少し準備が必要である。最初にARIMA(
)モデルと呼ぶ。この数式を書きおろすには少し準備が必要である。最初にARIMA(![]() )モデルを考える。これはARMA(
)モデルを考える。これはARMA(![]() )モデルに等しいから
)モデルに等しいから
(2) ![]()
と書ける。ここで、ラグ演算子![]() を次式で導入する。
を次式で導入する。
![]()
![]() は、時刻を1つ昔に戻す(Backword)演算子である。この演算子を使えば
は、時刻を1つ昔に戻す(Backword)演算子である。この演算子を使えば![]() に対しても
に対しても![]() と書ける。これらを式(2)に代入すると
と書ける。これらを式(2)に代入すると
![]()
(3) ![]()
を得る。式(3)がARIMA(![]() )モデルを表す式である。ARIMA(
)モデルを表す式である。ARIMA(![]() )モデルは1階差分系列のARIMA(1,0,1)であるから、
)モデルは1階差分系列のARIMA(1,0,1)であるから、![]() を
を![]() に置き換えれば良い。
に置き換えれば良い。
![]()
これが、ARIMA(![]() )モデルを記述する式である。一般のARIMA(
)モデルを記述する式である。一般のARIMA(![]() )モデルの場合は
)モデルの場合は
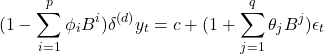
となる。ここで、![]() である。かなり複雑な式になる。
である。かなり複雑な式になる。
SARIMAモデル
自己相関(「時系列解析-1」と「時系列解析-2」で説明した)のグラフを描画した際に、顕著な周期性(季節成分)が見出されることがある。
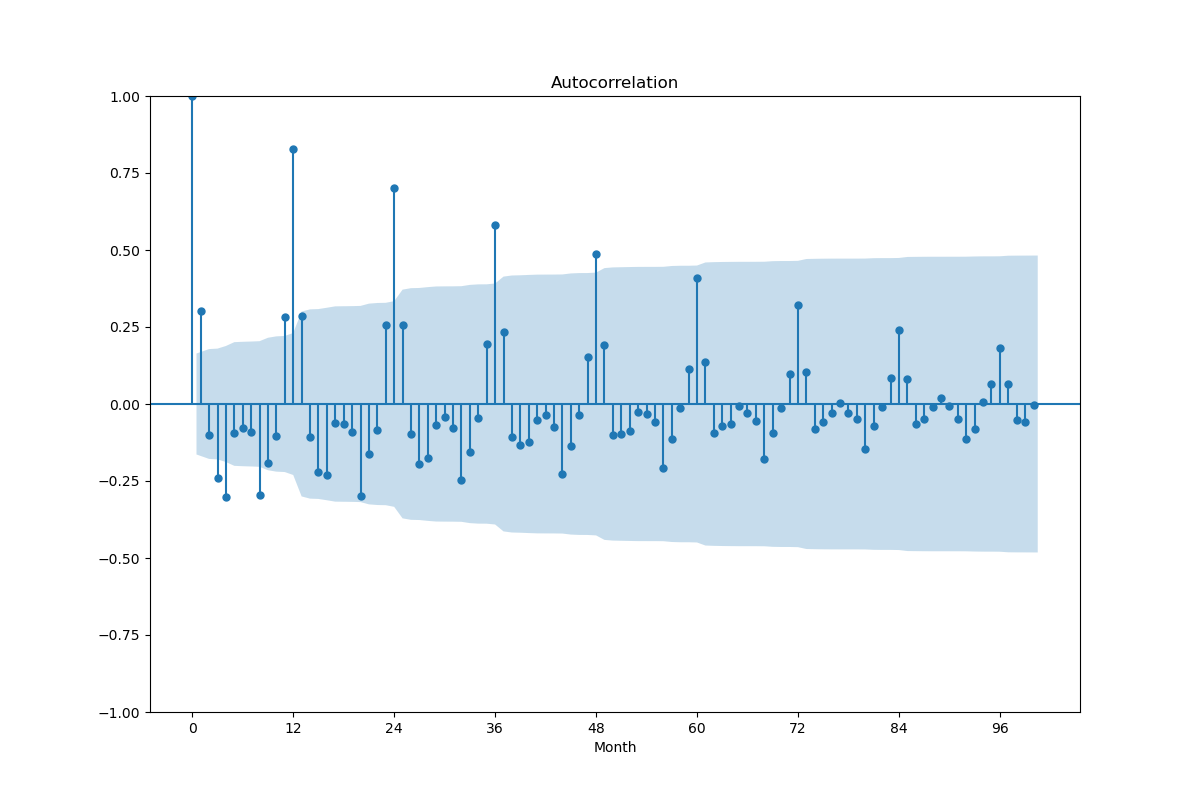
図2
例えば上図は飛行機の乗客数データ(データ解析で良く使われるデータセットのひとつ)の自己相関図である(元データはここにある)。図から12か月の周期を読み取ることができる。この周期を![]() とする。このとき、
とする。このとき、![]() と
と![]() の差を取った差分系列を考える(
の差を取った差分系列を考える(![]() )。新たな系列データ
)。新たな系列データ![]() に対するARIMAモデルを考えると、次数
に対するARIMAモデルを考えると、次数![]() に相当する新たな次数
に相当する新たな次数![]() を定義することができる。系列データ
を定義することができる。系列データ![]() に対するARIMAモデルと系列データ
に対するARIMAモデルと系列データ![]() に対するARIMAモデルを組み合わせたモデルをSARIMAモデルと呼び、SARIMA(
に対するARIMAモデルを組み合わせたモデルをSARIMAモデルと呼び、SARIMA(![]() )(
)(![]() )
)![]() と表記する。具体的な式の形は ARIMA(
と表記する。具体的な式の形は ARIMA(![]() )に輪をかけて複雑になるので割愛する。興味ある方は下に掲載した参考文献の2を見てほしい。
)に輪をかけて複雑になるので割愛する。興味ある方は下に掲載した参考文献の2を見てほしい。
まとめ
今回は、AR過程とMA過程を合わせたARMAモデルを紹介した。さらに、ARMAを定常過程に適用するためのARIMAモデルと周期性を考慮したSARIMAモデルも説明した。次回は実際のデータにSARIMAを適用する。

