はじめに
今回は、最小二乗法を入り口にして、最尤推定、MAP推定、リッジ回帰について説明したい。
最小二乗法
入力データ ![]() と出力データ
と出力データ ![]() が与えられているとする。ここで、
が与えられているとする。ここで、![]() は
は![]() 次元列ベクトルである。これらを用いて次の量を定義する。
次元列ベクトルである。これらを用いて次の量を定義する。
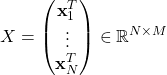
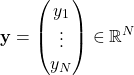
![]() は転置を表す。
は転置を表す。![]() は
は![]() 行列、
行列、![]() は
は![]() 次元列ベクトルである。後の計算を簡単にするため、次式が成り立つとする。
次元列ベクトルである。後の計算を簡単にするため、次式が成り立つとする。
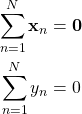
すなわち、データは前処理により「中心化」されている。このとき次の線形回帰モデルを考える。
(1) ![]()
ここで、![]() 、
、![]() である。
である。![]() は誤差ベクトル(ノイズ)を表す。式(1)は
は誤差ベクトル(ノイズ)を表す。式(1)は
![]()
をまとめて書いたものである。![]() は中心化されているので、式(1)に定数項(バイアス項)は存在しないことに注意する。さて、
は中心化されているので、式(1)に定数項(バイアス項)は存在しないことに注意する。さて、![]() が最小になるように
が最小になるように![]() を決めることを考える。その際、次の二乗誤差を用いる。
を決めることを考える。その際、次の二乗誤差を用いる。
(2) 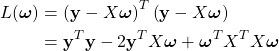
(3) ![]()
を得る。これより
![]()
を得る。![]() の逆行列が存在すれば
の逆行列が存在すれば
![]()
となる。ここまでの手順が最小二乗法である。すなわち、二乗誤差を最小にする![]() を決定する手法である。
を決定する手法である。
最尤推定
最尤推定(Maximum Likelihood Estimation)の入り口は確率である。最初に![]() が同時に実現する確率
が同時に実現する確率![]() を考える。このとき、ベイズの定理より
を考える。このとき、ベイズの定理より
![]()
が成り立つ。左辺は、観測値![]() が与えられたとき
が与えられたとき![]() が実現する確率を表す。この確率を最大にするような
が実現する確率を表す。この確率を最大にするような![]() を求めることが目的である。
を求めることが目的である。
さて、右辺の分母にある確率は![]() に依存しないので定数として扱うことができる。
に依存しないので定数として扱うことができる。
(4) ![]()
(5) ![]()
右辺は、![]() が実現しているとき
が実現しているとき![]() が実現する確率であるが、この確率を
が実現する確率であるが、この確率を![]() の関数と見るとき尤度関数と呼ぶ。尤度関数を最大にするように
の関数と見るとき尤度関数と呼ぶ。尤度関数を最大にするように![]() を決める手法を最尤推定と言う。
を決める手法を最尤推定と言う。
各観測値は独立に同一の分布から得られると仮定すると
(6) 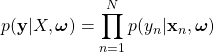
(7) 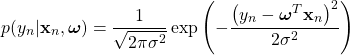
式(7)を式(6)に代入し、その値を最大にするような![]() を求めることが目的であるが、そのまま扱うより対数をとり最大値を探した方が楽である。そこで次の対数尤度を定義する。
を求めることが目的であるが、そのまま扱うより対数をとり最大値を探した方が楽である。そこで次の対数尤度を定義する。
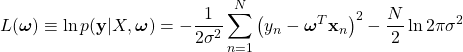
右辺を最大化することは
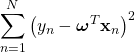
を最小化することと等価である。これは先に考えた最小二乗法の式(2)である。すなわち、最小二乗法とは、尤度関数として正規分布を採用した最尤推定と同じであることが分かる。
MAP推定とリッジ回帰
ここまでの議論で最小二乗法と最尤推定が等価であることを示した。そして求めたい![]() の値は次式で与えられた。
の値は次式で与えられた。
![]()
しかし、![]() が逆行列を持たない場合、
が逆行列を持たない場合、![]() を求めることができない。
を求めることができない。![]() が逆行列を持たない代表的な例として、
が逆行列を持たない代表的な例として、![]() を構成する2つのデータ
を構成する2つのデータ![]() が線形従属となる場合を挙げることができる。このような場合を多重共線性があると言い、このとき
が線形従属となる場合を挙げることができる。このような場合を多重共線性があると言い、このとき![]() の行列式と
の行列式と![]() の行列式は0になる。
の行列式は0になる。
多重共線性を回避する1つの方法としてMAP推定(Maximum A Posteriori Estimation)がある。MAP推定では、式(4)で定数とみなした![]() に対しても正規分布を与える。
に対しても正規分布を与える。
![]()
そして、先と同じように対数尤度を最大化することを考える。
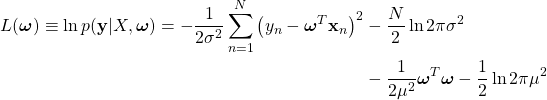
![]() に依存しない項を無視して整理すると
に依存しない項を無視して整理すると
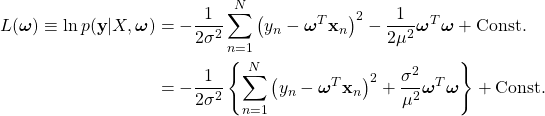
(8) 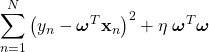
を最小化すれば良いことになる。この解も解析的に求めることができて
![]()
を得る。ここで、![]() は単位行列である。行列
は単位行列である。行列![]() に対しては、
に対しては、![]() に多重共線性の問題があっても常に逆行列を計算することができる。すなわち、MAP推定は多重共線性の問題を回避できる手法である。ところで、式(8)は最小二乗法の式に正則化項(
に多重共線性の問題があっても常に逆行列を計算することができる。すなわち、MAP推定は多重共線性の問題を回避できる手法である。ところで、式(8)は最小二乗法の式に正則化項(![]() )を追加した式とみなすこともできる。この立場からの定式化をリッジ回帰と呼ぶ。つまり、この例においてMAP推定とリッジ回帰は等価である。
)を追加した式とみなすこともできる。この立場からの定式化をリッジ回帰と呼ぶ。つまり、この例においてMAP推定とリッジ回帰は等価である。
パラメータ![]() は、あらかじめ決めておくパラメータ(ハイパーパラメータ)である。このパラメータを決めるにはまた別の議論が必要であるが、今回は割愛する。
は、あらかじめ決めておくパラメータ(ハイパーパラメータ)である。このパラメータを決めるにはまた別の議論が必要であるが、今回は割愛する。
まとめ
今回は、最小二乗法から始めて最尤推定、MAP推定、リッジ回帰について説明した。お互いに関連した手法であること、入り口は異なるが同じ結果を得る手法であることを示した。
今回の説明では、![]() が逆行列を持たない例として多重共線性だけを考えたが、実はもうひとつ重要な例がある。
が逆行列を持たない例として多重共線性だけを考えたが、実はもうひとつ重要な例がある。![]() となる場合である。すなわち、サンプル数
となる場合である。すなわち、サンプル数![]() の方が
の方が![]() の次元数
の次元数![]() より少なくなる場合である。このとき、多重共線性の有無とは無関係に
より少なくなる場合である。このとき、多重共線性の有無とは無関係に![]() の逆行列を計算できない。この場合の対処法の説明は機会を改めたい。
の逆行列を計算できない。この場合の対処法の説明は機会を改めたい。

