はじめに
今回は、ベイズ推論の1手法である変分推論について解説する。具体例としてガウス混合モデルを用いたクラスタリングを行い、実際の計算結果を示す。
変分推論
観測値を![]() 、潜在変数とパラメータを合わせて
、潜在変数とパラメータを合わせて![]() とおく。ただし、
とおく。ただし、![]() である。このとき、同時確率分布
である。このとき、同時確率分布 ![]() を考え、ベイズの定理を適用すると
を考え、ベイズの定理を適用すると
(1) ![]()
を得る。ベイズ推論の目的は事後確率![]() を求めることである。一般に、
を求めることである。一般に、![]() を厳密に求めることはできないので、近似関数
を厳密に求めることはできないので、近似関数![]() を考える。次式
を考える。次式![]() (ELBO:Evidence Lower Bound)が最大になるように
(ELBO:Evidence Lower Bound)が最大になるように![]() を最適化する手法を変分推論と呼ぶ。
を最適化する手法を変分推論と呼ぶ。
(2) ![]()
実は、ELBOの最大化とKLダイバージェンス
(3) ![]()
を最小化することは等価である。従って、KLダイバージェンスの最小化を用いて変分推論を定式化することもできるが、今回はELBOの最大化を利用して定式化する。
平均場近似
上で個々のデータの集まりとして![]() を定義したが、ここでは複数のパラメータ(と潜在変数)の集まりとして
を定義したが、ここでは複数のパラメータ(と潜在変数)の集まりとして![]() を考える。
を考える。![]() を近似するとき最も良く使われる手法が次の平均場近似である。
を近似するとき最も良く使われる手法が次の平均場近似である。
(4) 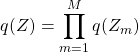
この近似は、![]() 間の相関を無視し、それぞれが独立に生成されると仮定したものである。最適な各関数
間の相関を無視し、それぞれが独立に生成されると仮定したものである。最適な各関数 ![]() を求めるには、
を求めるには、![]() を
を![]() で汎関数微分すれば良い。このことを念頭において式(4)を式(2)に代入すると
で汎関数微分すれば良い。このことを念頭において式(4)を式(2)に代入すると
(5) 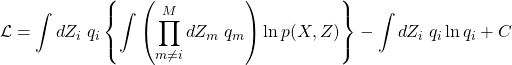
を得る。煩雑さを避けるため![]() とした。
とした。![]() は
は![]() に依存しない全ての項をまとめたものである。いま次の期待値
に依存しない全ての項をまとめたものである。いま次の期待値
(6) ![Rendered by QuickLaTeX.com \begin{equation*} \mathbb{E}_{m\neq i}\left[\ln{p(X,Z)}\right]=\int \left(\prod_{m\neq i}^{M}dZ_m\;q_m\right)\ln{p(X,Z)} \end{equation*}](/wp-content/ql-cache/quicklatex.com-19c0a9c704dcd359d679a6c25e216d70_l3.png)
を定義すると
(7) ![]()
と書くことができる。上式を![]() で汎関数微分したものを0と置くことにより次式を得る。
で汎関数微分したものを0と置くことにより次式を得る。
(8) ![]()
これが近似関数![]() を求める式である。
を求める式である。![]() であるから次の反復アルゴリズムで計算することになる。
であるから次の反復アルゴリズムで計算することになる。
ガウス混合モデル
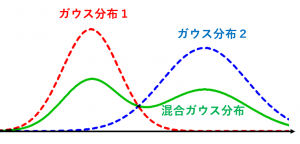
混合モデルとは複数の確率分布(クラスタ)を用いてひとつの確率分布を表現するモデルである。具体的に説明するため、下図を考える。
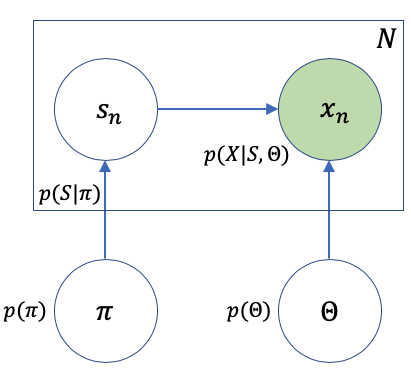
この図は以下のことを表現している。
(9) 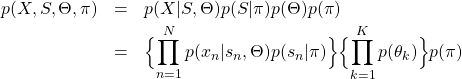
例えば、クラスタ(![]() )をガウス分布で表す場合、複数のガウス分布を適当な比率(
)をガウス分布で表す場合、複数のガウス分布を適当な比率(![]() )で混ぜ合わせて目的の分布を近似することになる(下図)。このモデルをガウス混合モデル(Gaussian Mixture Model:GMM)と呼ぶ。
)で混ぜ合わせて目的の分布を近似することになる(下図)。このモデルをガウス混合モデル(Gaussian Mixture Model:GMM)と呼ぶ。
ガウス混合モデルの変分推論
ガウス混合モデルに平均場近似を適用する。出発式となるのは式(8)で示した次式である。
(10) ![]()
![]() に相当する変数は
に相当する変数は![]() である。ガウス分布を考えるので
である。ガウス分布を考えるので ![]() と置ける。ここで
と置ける。ここで![]() は平均、
は平均、![]() は精度行列である。いま観測値
は精度行列である。いま観測値![]() の次元を
の次元を![]() としているので
としているので![]() の次元も
の次元も![]() である。また、行列
である。また、行列![]() は
は![]() のサイズを持つ。
のサイズを持つ。
式(10)より次の式を得る。
(11) ![]()
この2式を辛抱強く変形していくと、事後確率 ![]() についての式を得る。詳細はPRMLや須山本を見てほしい。これら4式はお互いに依存しているので既に述べたように反復して解くことになる。
についての式を得る。詳細はPRMLや須山本を見てほしい。これら4式はお互いに依存しているので既に述べたように反復して解くことになる。
計算結果
観測値の次元![]() を2としてPythonによる実装を行った。今回はベイズ推論関係のライブラリを使わず、フルスクラッチで実装した。参照した文献は、須山本のp144から始まる「4.4 ガウス混合モデルにおける推論」である。私のソースコードはここにある。最初に適当なガウス分布を用いて観測値を作成する(下図参照)。
を2としてPythonによる実装を行った。今回はベイズ推論関係のライブラリを使わず、フルスクラッチで実装した。参照した文献は、須山本のp144から始まる「4.4 ガウス混合モデルにおける推論」である。私のソースコードはここにある。最初に適当なガウス分布を用いて観測値を作成する(下図参照)。
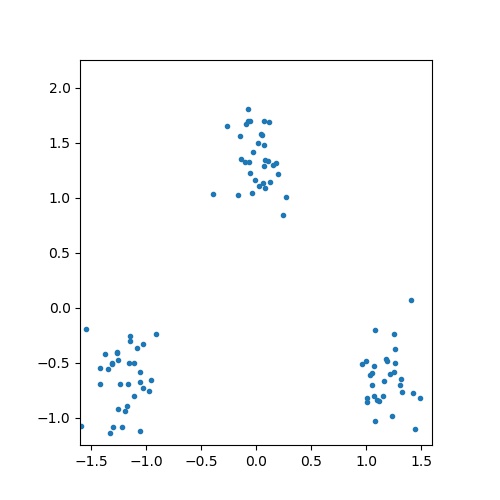
これを入力値として、![]() として変分推論を行う。結果は以下の通り。
として変分推論を行う。結果は以下の通り。
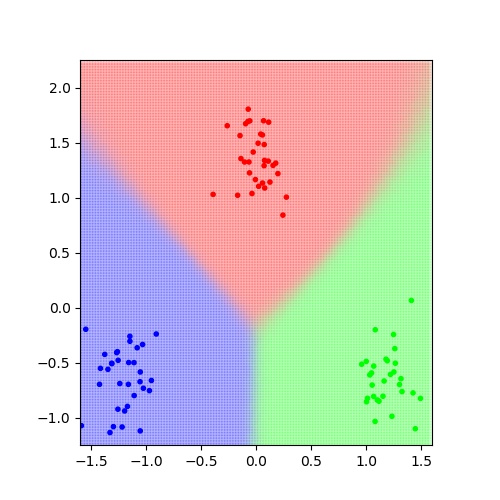
各クラスタを3色で示した。綺麗に分割できている。また、観測値以外の点についても、どのクラスタに属するかを確率として予測することができる。つまり、1点ごとに確率が求まるので、全平面を塗り分けることができる。今回は1点つき100回確率を求めその平均値を用いて色を決定した。図に見るように境界部分では色が混ざり連続的にもう一方の色へ変化していくことが分かる。このような変化を捉えることができるのがベイス推論の大きな特徴である。
別の観測値を考える。
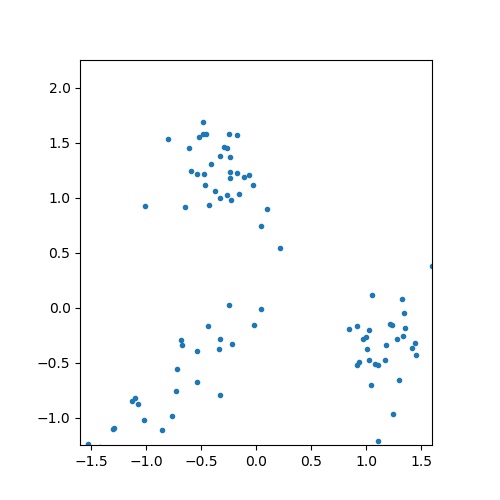
推論結果は以下の通り。
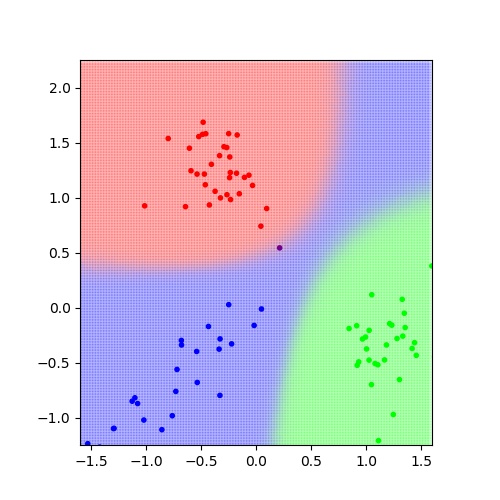
赤の境界近傍にある観測点の1つが紫色となっている。これは青である確率と赤で確率がほぼ互角となったためであろう。この図の注目すべき点は、右上の領域が青で塗られている点である。青の観測値は斜め方向に分散が大きいため、このように予測されたのである。単純に距離だけで判断するのであれば赤や緑で塗られるはずである。
以下、数値計算する上での注意点を列記する。
まとめ
今回は、ベイス推論の1手法である変分推論を紹介し、クラスタリングに適用した事例を示した。ベイズ推論自体は、回帰や分類問題など幅広く応用できる機械学習の手法である。深層学習に触発されたAIブームの中、ベイズ推論もまた注目されている。
参考文献
どちらも私のバイブルである。PRMLについては演習問題もおすすめです。