今回は次元削減の話です。
お世話になっております。長文しか書けないBBです。
次元削減と聞くと重力系の技のような印象ですが、機械学習では特徴量の項目数を少なくする処理を指します。特徴量とは機械学習を行う際に使う数値データのことです。特徴量が例えば「幅」という項目だけならば1次元のデータ、「幅」と「奥行」なら2次元のデータとなります。
なら3次元は「幅」「奥行」「高さ」、4次元目は「時間」??5次元目なんか想像もつかない……となる方もいらっしゃるかもしれませんので補足を。次元を持たせる項目はぶっちゃけ何でもいいです。単純な話、「親指の長さ」「人差し指の長さ」と考えれば片手で5次元、両手で10次元の項目を定義したことになります。特徴量の次元なんてそんなもんだととらえてください。
次元削減でデータをシンプルに
機械学習でも特徴量が多すぎると精度が悪くなってしまうことがあります。いわゆる「次元の呪い」と呼ばれる現象ですが、小難しいことを抜きにしても高次元のデータというのは扱いにくいものです。せめて3次元までのデータであれば図に落とし込むことができますので視覚的にも傾向を把握しやすくなります。データの次元数を削減する手法として、とりあえず取っ付き辛いと評判(僕個人の感想)の主成分分析が今回のお題です。
簡単に言ってしまえば主成分分析とはなんなのか
主成分分析ってもうすでに小難しそうな響きですが、なにをするのかイメージすることは難しくないのでまずは図で理解してきましょう。
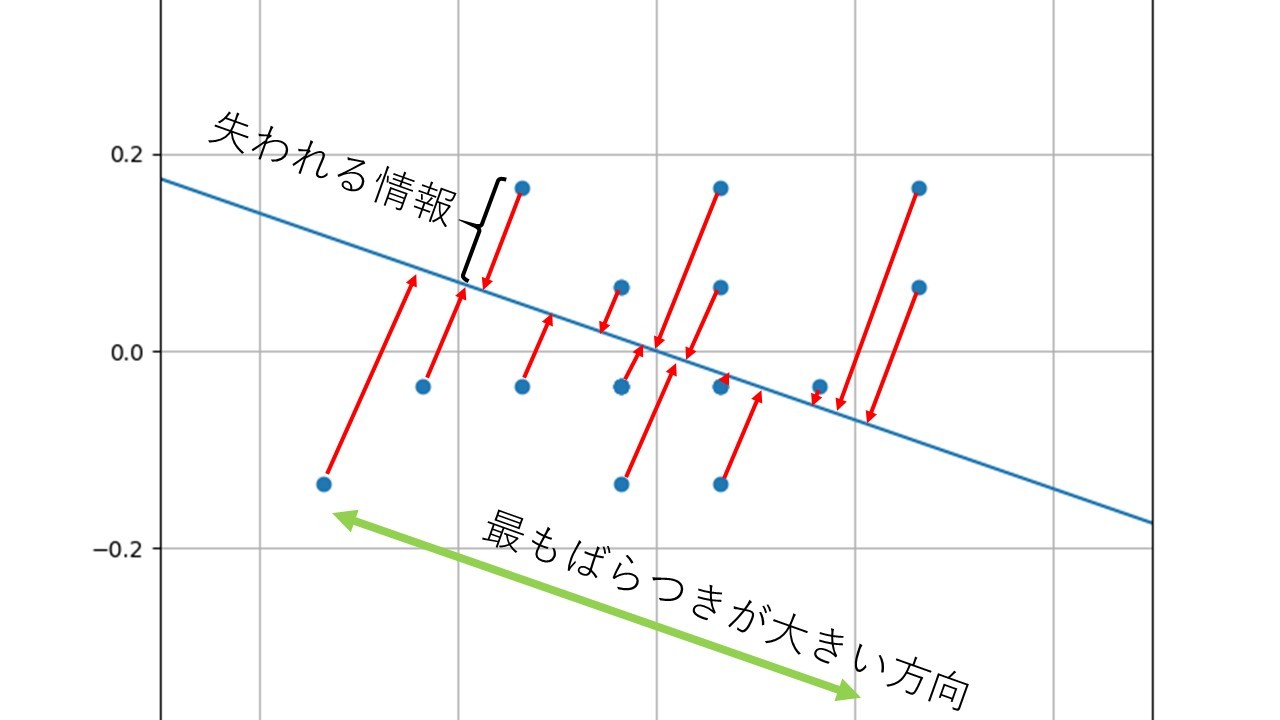
散布図の中に青い直線が引かれており、それぞれのデータから青直線に向かって直角になるように赤い矢印が下ろしてあります。主成分分析ではこの青直線とそれぞれの赤矢印がぶつかったところにデータを写し取っていきます。この処理によってそれぞれの点が青直線のどこにあるか1つの数値で決まることになります。つまり、XとYの2次元だったデータが、1次元のデータに次元が削減されたことになりますね。ではこの青直線、いったいどうやって決めるのかというと、図に示したようにそれぞれのデータが1番ばらつくように引いた線になります。なぜこんな定義になっているのかといえば、「直線に写し取った結果失う情報量が最も少なくなるようにする為」というのが答えになります。この場合、失われる情報というのは直線とそれぞれの点の距離(赤矢印)になります。これが主成分分析の第1主成分の定義です。
第1とついている以上、第2もあるのはうすうす感づいているのではないでしょうか。では第2主成分は何なのか。2番目にばらつきが大きくなる線か?とお考えの人も多いでしょうが残念。僕もネットの拾い読みで信じていた口ですが、これはちょっと考えればおかしいことに気づきます。なぜなら2番目にばらつきが大きい直線なんて、第1主成分で使った青直線をほんのちょっとずらせばいいだけということになってしまいます。では何をもって第2主成分というのか、それは第1主成分が捨ててしまった情報、つまり赤矢印方向の直線に写し取った情報なのです。図にしたらこんな感じです。
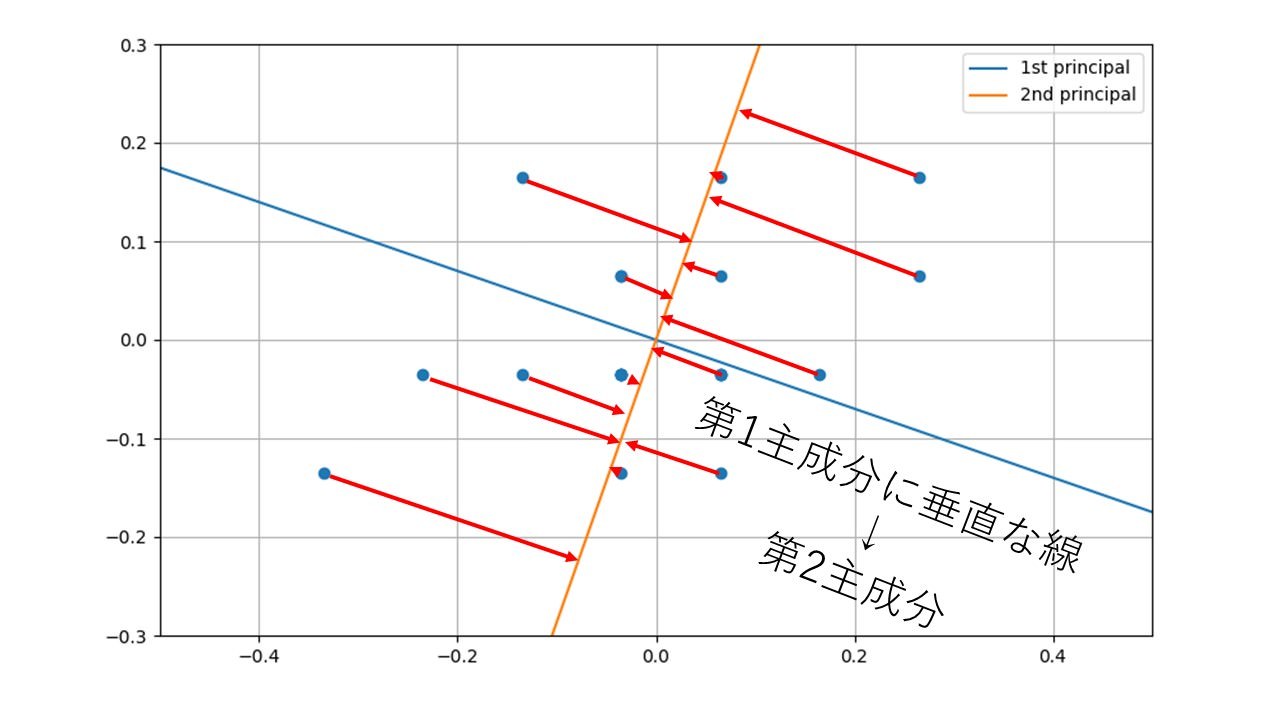
この図で使ったデータは2次元のデータなので第1主成分と第2主成分でその位置を情報を失うことなく(失わないように第2主成分を定義したので)完全に表すことができます。要するに主成分分析とは図の横軸と縦軸を青とオレンジで示した軸にあわせて回転させただけだったわけです。
これで分かったことがあります。今回、扱ったのは2次元のデータですので縦横の2軸を回転させることでできる第1、第2主成分が存在していましたが、もし取り扱ったのが3次元データであればどうだったでしょうか。縦横奥行の3軸を回転させることで主成分分析が行われていたと思いませんか?そう、3次元データでは第3主成分まで定義することができるわけなのです。もっと一般的にいえばM次元のデータは第M主成分まで定義できてしまうということがわかりますね。
NumPyで実装する主成分分析
さて、主成分分析についてのイメージがついたところでNumPyであっさり実装してみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
#!/usr/bin/env python3 # -*- coding: utf-8 -*- import numpy as np from matplotlib import pyplot as plt from sklearn.datasets import load_iris def pca_use_org(data): # ##################### 主成分分析 ######################## # 共分散行列を求める cov_matrix = np.cov(data, rowvar=False) # 固有値と固有ベクトルを取得する l, v = np.linalg.eig(cov_matrix) # 固有値を大きい順に並べる l_index = np.argsort(l)[::-1] l_ = l[l_index] v_ = v[:, l_index] # 固有ベクトルを使ってデータを変換する data_trans = np.dot(data, v_) return data_trans, v_ if __name__ == "__main__": # ###################### データ作成 ######################## # データセットから2次元データを切り出す d_index = [0, 2] iris = load_iris() data = iris.data data = data[:, d_index] # データ全体の平均を0にする print('data=', data) data -= data.mean(axis=0) print('data=', data) # #################### 主成分分析開始 ####################### # 自作関数(numpyはその限りではない)でPCA data_trans, v = pca_use_org(data) # ###################### 作図準備 ########################### # 変換軸となるベクトルを描画用の変数に格納 vec_s = [0, 0] vec_1st_e = [2*v[0, 0], 2*v[0, 1]] vec_2nd_e = [2*v[1, 0], 2*v[1, 1]] # ######################## 作図開始 ######################## # -------------------- 変換前データと変換軸ベクトル --------- plt.figure(figsize=[8, 8]) plt.xlim(-4, 4) plt.ylim(-4, 4) plt.quiver(vec_s[0], vec_s[1], vec_1st_e[0], vec_1st_e[1], angles='xy', scale_units='xy', scale=1, color='r', label='1st') plt.quiver(vec_s[0], vec_s[1], vec_2nd_e[0], vec_2nd_e[1], angles='xy', scale_units='xy', scale=1, color='b', label='2nd') plt.grid() plt.legend() plt.scatter(data[:, 0], data[:, 1], c=iris.target) plt.savefig('charts/fig-3.png') # -------------- 変換後データ、第1主成分、第2主成分 --------- plt.figure(figsize=[8, 8]) plt.subplot2grid((4, 1), (0, 0), rowspan=2) plt.title('1st principal - 2nd principal') plt.grid() plt.scatter(data_trans[:, 0], data_trans[:, 1], c=iris.target) plt.subplot2grid((4, 1), (2, 0)) plt.tick_params(labelleft="off", left="off") plt.title('1st principal') plt.grid() plt.scatter(data_trans[:, 0], np.zeros(len(data_trans[:, 0])), c=iris.target) plt.subplot2grid((4, 1), (3, 0)) plt.title('2nd principal') plt.grid() plt.tick_params(labelleft="off", left="off") plt.scatter(data_trans[:, 1], np.zeros(len(data_trans[:, 1])), c=iris.target) plt.tight_layout() plt.show() |
実行結果
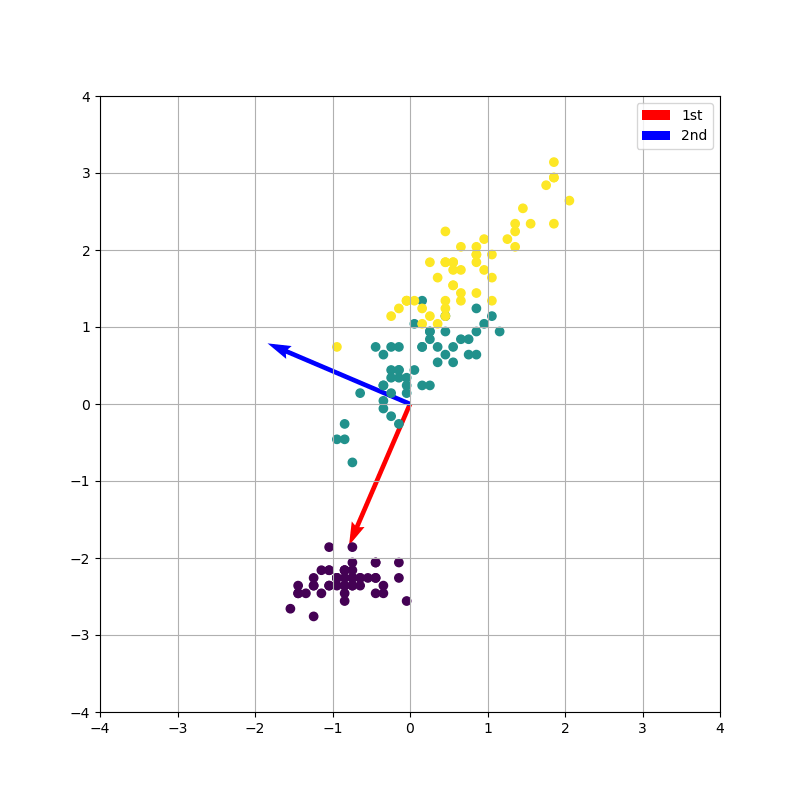
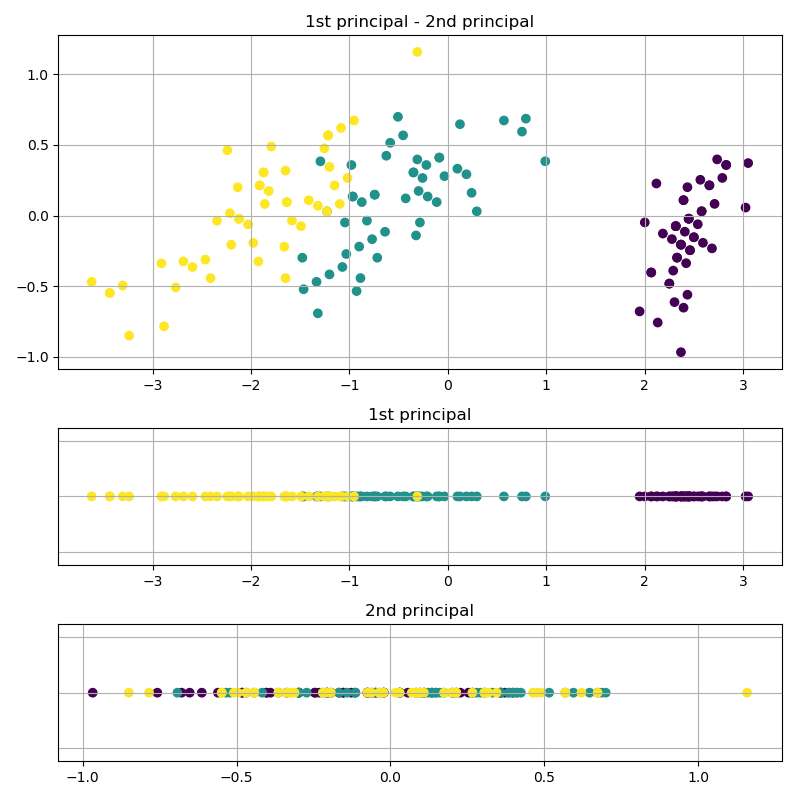
計算に使ったデータはおなじみscikit-learnのirisデータセットです。実行結果の図は1枚目が変換前のデータに変換用の軸を上書きしたものです。2枚目の上の図は第1主成分を横軸に、第2主成分を縦軸に取った図です。2枚目の中下段は変換用の軸にデータを射影した結果です。プロットはラベル毎に色分けされており、3種類のクラスに分けられます。うまいこと、変換軸をもとに変換できていることが分かります。また、射影した図を見てみると第1主成分のデータでは3種類のクラスが分けられていますが、第2主成分のデータはごちゃごちゃに混ざってしまっています。
上記はirisデータセットを切り出して2次元データとして扱っていますが、全部使うと4次元のデータになります。4次元データ全てを使った結果がこちらです。
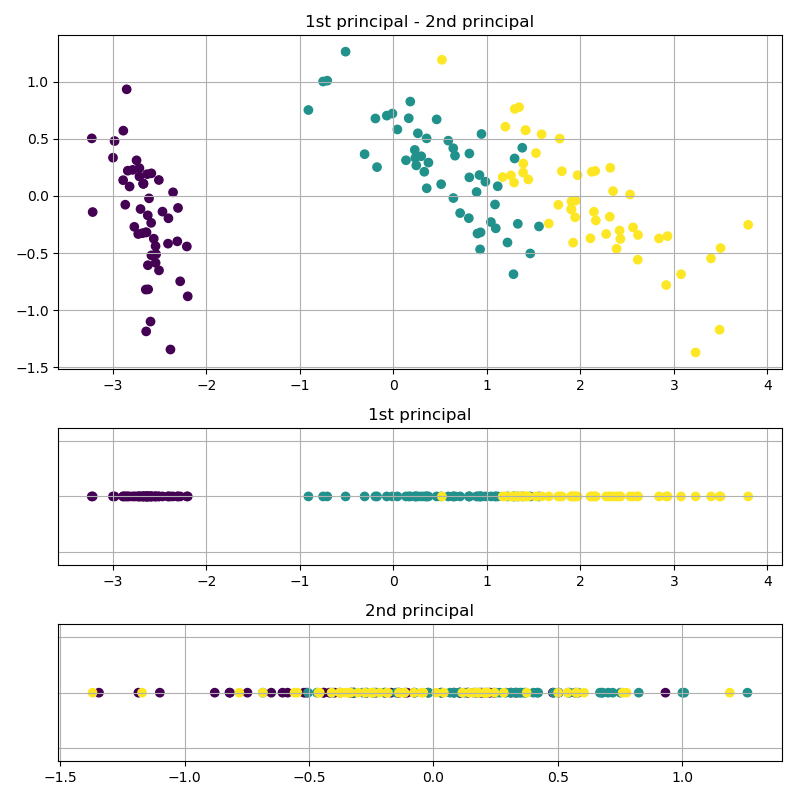
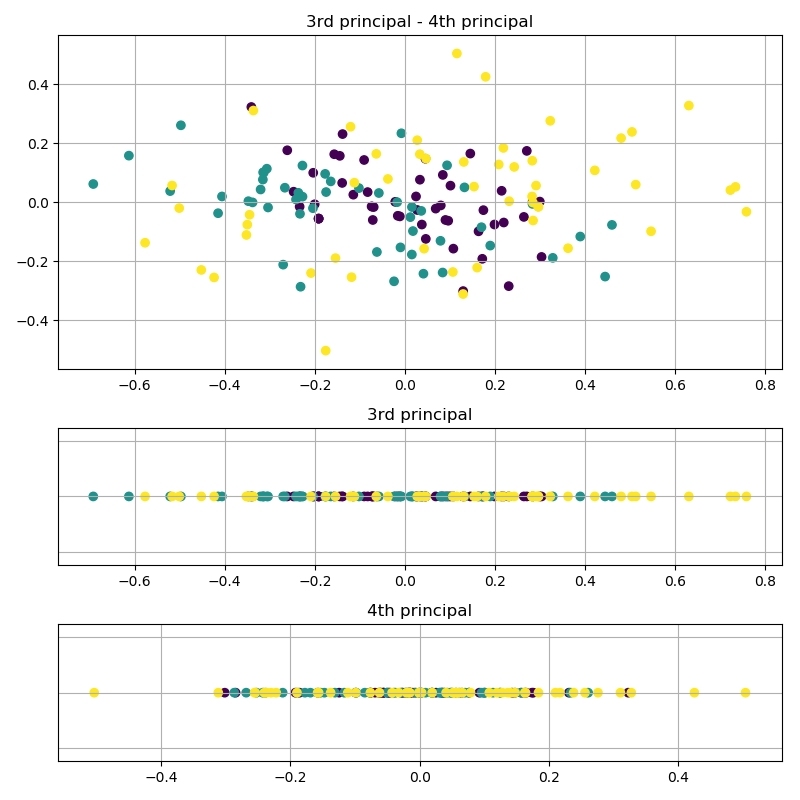
4次元データを使っていますので、第1~第4主成分まで計算することができます。それぞれの軸に射影した図を見てみるとやはり第1主成分ではクラス分けができそうですが、第2~第4主成分はごちゃついてしまってクラス分類どころではなさそうですね。
さて、実際に数値を使って図を作ってみましたが主成分分析のイメージは固まってきたでしょうか。あっさりしたソースコードになっていますがいったい何をやっているのか、次の章で数式を見ながらコードの内容を理解していきましょう。
数式で理解する主成分分析
主成分分析に取り掛かるまでにいくつか知っておきたいことがありますので、ちょちょっとまとめていきます。
分散と共分散
先の説明で少し触れましたが、第1主成分を射影する軸の方向はデータが最もばらつく方向にとると説明しました。このデータのばらつきの指標に分散:![]() があります。式で書くとこうなります。
があります。式で書くとこうなります。
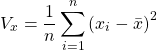
日本語に訳すと、1~n個までのデータ:![]() からそれぞれ平均:
からそれぞれ平均:![]() を引いたもの(これを偏差といいます)の2乗を全部足し合わせてnで割った数が分散となります。式を見る通り、平均から離れているデータが多いほど分散が大きくなります。逆に一定の値をとるようなデータであれば分散は0に近づいていきます。また、
を引いたもの(これを偏差といいます)の2乗を全部足し合わせてnで割った数が分散となります。式を見る通り、平均から離れているデータが多いほど分散が大きくなります。逆に一定の値をとるようなデータであれば分散は0に近づいていきます。また、![]() は2乗をとっていますので、
は2乗をとっていますので、![]() が実数である限りは分散は0以上となります。
が実数である限りは分散は0以上となります。
分散は![]() という1つのデータのみ扱いましたが、今度は別のデータ
という1つのデータのみ扱いましたが、今度は別のデータ![]() が登場します。この2つから共分散:
が登場します。この2つから共分散:![]() を計算します。
を計算します。
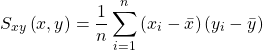
分散の式に似ていますが、共分散は![]() と
と![]() の偏差のかけ合わせた数を足し合わせています。同じ数の2乗の足し合わせだった分散とは違って共分散は正の値も負の値もどちらもとることができます。共分散は2つのデータがどのような傾向にあるかを簡単に示す指標になっています。例えば
の偏差のかけ合わせた数を足し合わせています。同じ数の2乗の足し合わせだった分散とは違って共分散は正の値も負の値もどちらもとることができます。共分散は2つのデータがどのような傾向にあるかを簡単に示す指標になっています。例えば![]() が正の値をとるとき、
が正の値をとるとき、![]() が負の値をとるとすると共分散は負の値となります。両方とも正の値をとる場合、分散は正の値となるわけです。グラフにすると傾きが正の分布は共分散は正、傾きが負の分布は共分散が負になりやすいといえます。
が負の値をとるとすると共分散は負の値となります。両方とも正の値をとる場合、分散は正の値となるわけです。グラフにすると傾きが正の分布は共分散は正、傾きが負の分布は共分散が負になりやすいといえます。
分散共分散行列
高次元のデータを考えたときに分散、共分散の組み合わせがたくさんになってしまい書くのが面倒になりますので行列にまとめてしまおうというのが分散共分散行列です。わかりやすくする為、ここでは![]() と
と![]() の2次元データを考えていきましょう。まずはこんな行列を定義します。
の2次元データを考えていきましょう。まずはこんな行列を定義します。
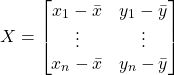
![]() と
と![]() の偏差を1~nまでがんがん並べていっています。その行列にこんなことをします。行列式の計算はちょっと癖がありますので、よくわからないという方は前回記事を参考にしてみてください。
の偏差を1~nまでがんがん並べていっています。その行列にこんなことをします。行列式の計算はちょっと癖がありますので、よくわからないという方は前回記事を参考にしてみてください。
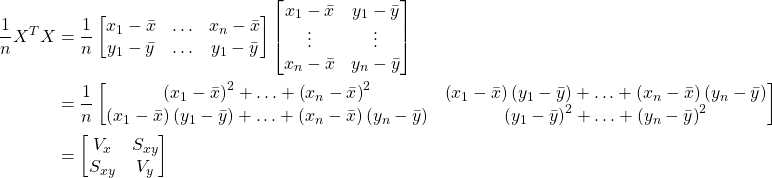
途中式は面倒でしたが見ごとに![]() と
と![]() の分散、共分散からなる行列を計算することができました。
の分散、共分散からなる行列を計算することができました。
主成分分析
前置きが長くなりましたがいよいよ主成分分析について考えていきたいと思います。今回も![]() と
と![]() の2次元データを使って考えていきましょう。主成分分析は2次元データの場合、縦軸と横軸を回転させた新しい座標系にデータを変換させる処理だということは既に説明しました。では変換後のデータを
の2次元データを使って考えていきましょう。主成分分析は2次元データの場合、縦軸と横軸を回転させた新しい座標系にデータを変換させる処理だということは既に説明しました。では変換後のデータを![]() と置くと
と置くと![]() と
と![]() の関係はこのように表すことができます。
の関係はこのように表すことができます。![]() は第1主成分なのか、第2主成分なのか気になる方もいるかもしれませんが、いったん心の中にしまってください。
は第1主成分なのか、第2主成分なのか気になる方もいるかもしれませんが、いったん心の中にしまってください。
(1) ![]()
ここでおもむろに![]() の分散:
の分散:![]() を求めてみます。お忘れかもしれませんが、この分散が最大になるよう
を求めてみます。お忘れかもしれませんが、この分散が最大になるよう![]() 、もとい変換に使われるパラメタの
、もとい変換に使われるパラメタの![]() 、
、![]() を求めることが主成分分析のポイントです。
を求めることが主成分分析のポイントです。![]() は以下の式で表せます。
は以下の式で表せます。
(2) 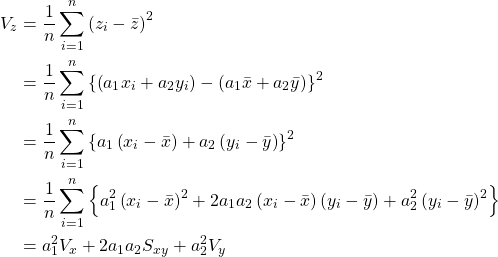
![]() を
を![]() と
と![]() の分散と共分散で表すことができました。
の分散と共分散で表すことができました。
今度は![]() と
と![]() についてもう少し考えてみます。
についてもう少し考えてみます。![]() と
と![]() をそれぞれ
をそれぞれ![]() と
と![]() と置きます。
と置きます。![]() と
と![]() はそれぞれ
はそれぞれ![]() に変換するための軸と
に変換するための軸と![]() 軸、
軸、![]() 軸との角度になっています。詳しいことは省きますが、このような
軸との角度になっています。詳しいことは省きますが、このような![]() と
と![]() を方向余弦といいます。このように定義することで
を方向余弦といいます。このように定義することで![]() と
と![]() には以下の関係というか制限ができます。
には以下の関係というか制限ができます。
(3) ![]()
式(2)と式(3)を使って、![]() が最大になる
が最大になる![]() と
と![]() を求めていきます。式(2)のような方程式と式(3)のような条件式がそろうとLagrangeの未定乗数法を使って答えを出すことができます。色々出てきて頭がパンクしてしまいましたが、もう少しです。
を求めていきます。式(2)のような方程式と式(3)のような条件式がそろうとLagrangeの未定乗数法を使って答えを出すことができます。色々出てきて頭がパンクしてしまいましたが、もう少しです。
Lagrangeの未定乗数法とは「求めたい変数の定義式:式(2) – ![]() x条件式:式(3)」を関数
x条件式:式(3)」を関数![]() として変数
として変数![]() 、
、![]() 、
、![]() の偏微分が0になるように
の偏微分が0になるように![]() 、
、![]() 、
、![]() を求めると
を求めると![]() が最大になるという魔法のような解法です。……お気持ちはわかります。この段階でしれっと変数が追加された憤りはひしひしと。では関数
が最大になるという魔法のような解法です。……お気持ちはわかります。この段階でしれっと変数が追加された憤りはひしひしと。では関数![]() と偏微分を解いていきましょう。
と偏微分を解いていきましょう。
関数![]()
(4) ![]()
偏微分式
(5) ![]()
(6) ![]()
(7) ![]()
式(7)は式(3)と同様なので用済みです。式(5)と式(6)は下のような行列式に書き換えることで知っている人なら知っている固有値問題になります。さっさとやってしまいましょう。
(8) ![]()
ここから分散共分散行列の固有方程式を解くことで![]() 、
、![]() 、
、![]() が求まります。詳細な解法についてはこちらを参照いただくとしてこの場合は以下の式を解いていきます。
が求まります。詳細な解法についてはこちらを参照いただくとしてこの場合は以下の式を解いていきます。
(9) 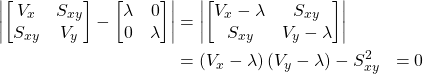
上記の通り![]() の2次方程式となりましたので、2つの
の2次方程式となりましたので、2つの![]() が求まったことになります。それぞれの
が求まったことになります。それぞれの![]() から
から![]() 、
、![]() を求めることができます。2つの
を求めることができます。2つの![]() のうち大きいほうが第1主成分、小さいほうが第2主成分となっており、それぞれに対応する
のうち大きいほうが第1主成分、小さいほうが第2主成分となっており、それぞれに対応する![]() 、
、![]() が変換軸を表すベクトルになっています。
が変換軸を表すベクトルになっています。
まとめ
長い……今回も長かった……。最初の方の内容は執筆していく過程で忘れてしまったので、主成分分析とはなんぞやというところを改めてまとめますね。
- 主成分分析は特徴量の次元削減に使われる手法だよ。
- 次元数Mの特徴量の場合、主成分分析は第1~第M主成分まで求められるよ。
- 分散共分散行列をいろいろやると最終的に固有値問題にいきつくよ。
多少、説明が荒くなった部分(最後のほう)もありますが、なんとなく主成分分析について警戒心がほぐれたと感じていただければ幸いです!

