はじめに
前回に引き続き時系列解析を解説する。今回はAR過程を紹介する。
AR(1)過程
我々が解析対象とする時系列データは、異なる時刻の間に何らかの関係(自己相関と呼ばれる)を持つのが普通である。この相関を記述する過程として前回はMA過程を取り上げた。今回はAR過程と呼ばれるものを紹介する。最初に1次のAR過程(AR(1)過程)を考える。これは次式で定義される。
(1) ![]()
![]() と
と![]() は任意の実数、
は任意の実数、![]() は分散
は分散![]() のホワイトノイズ(前回定義したノイズ)である。右辺を見ると1つ前の時刻の値
のホワイトノイズ(前回定義したノイズ)である。右辺を見ると1つ前の時刻の値![]() に依存していることが分かる。すなわち上式は自己回帰的(Auto Regression)に現在の値
に依存していることが分かる。すなわち上式は自己回帰的(Auto Regression)に現在の値![]() を決める式である。これがARと名付けられた理由である。2つ前までの自身の値に依存するなら2次のAR過程(AR(2)過程)、
を決める式である。これがARと名付けられた理由である。2つ前までの自身の値に依存するなら2次のAR過程(AR(2)過程)、![]() 個前までの自身の値に依存するなら
個前までの自身の値に依存するなら![]() 次のAR過程(AR(p)過程)となる。図1に
次のAR過程(AR(p)過程)となる。図1に![]() の値を変化させたときの式(1)の変化の様子を示す(コードはここにある)。
の値を変化させたときの式(1)の変化の様子を示す(コードはここにある)。
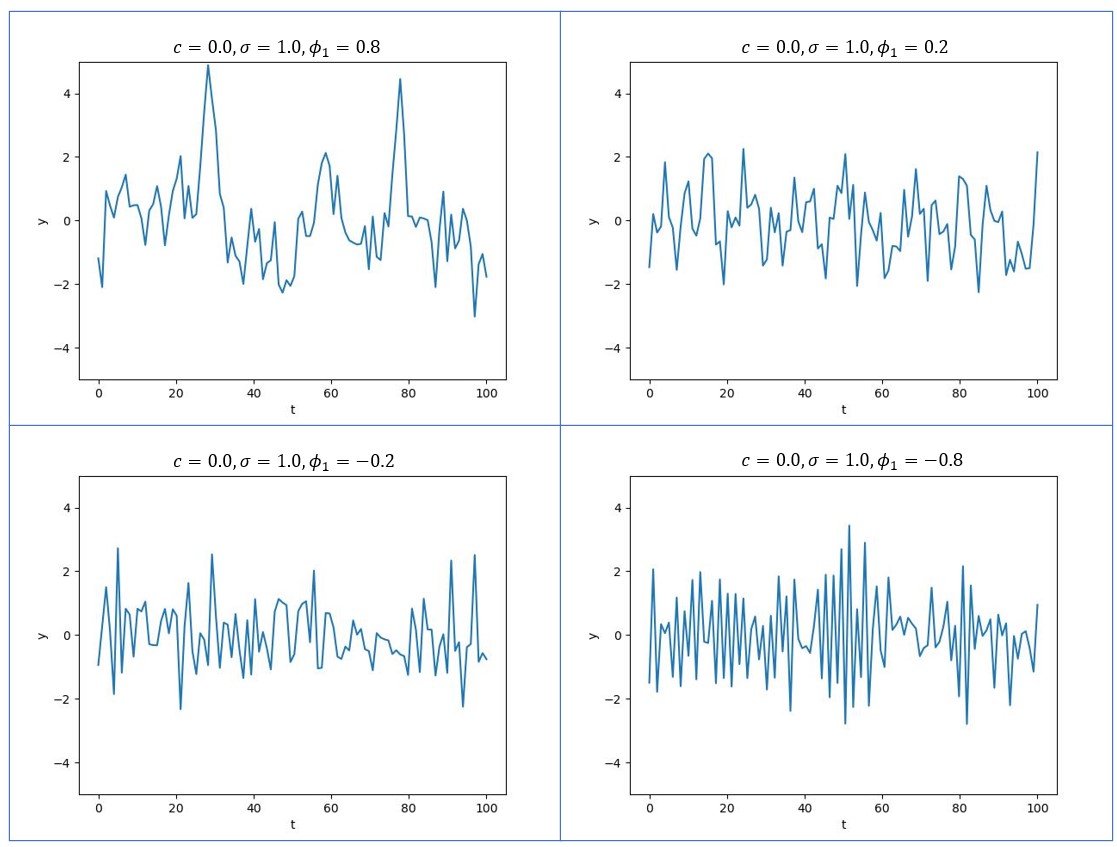
図1
![]() が負になると振動が激しくなる理由は、1つ前の値
が負になると振動が激しくなる理由は、1つ前の値![]() とは符号が逆になる傾向が強くなるためである(式(1)を参照)。さて、AR過程の顕著な振る舞いは
とは符号が逆になる傾向が強くなるためである(式(1)を参照)。さて、AR過程の顕著な振る舞いは![]() のときに起こる。図2に、
のときに起こる。図2に、![]() を
を![]() としたときのグラフを示す。
としたときのグラフを示す。
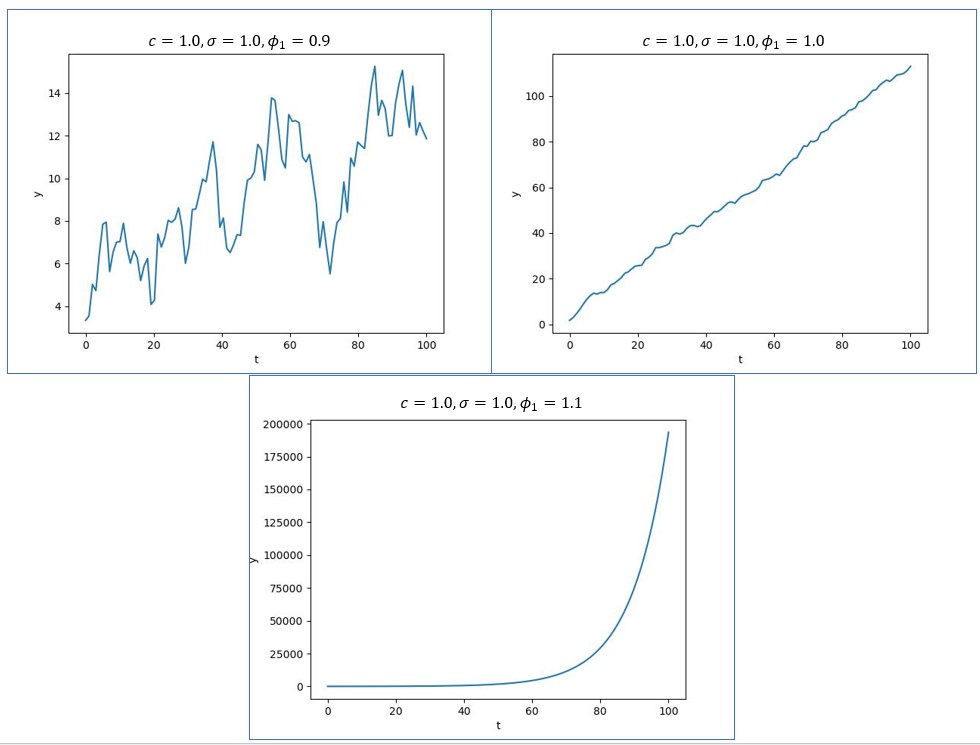
図2
上のグラフの振る舞いを理解するため、式(1)を自己回帰的に![]() 回代入する。
回代入する。
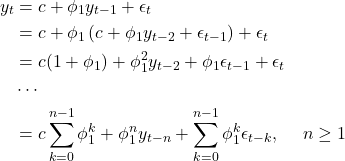
(2) 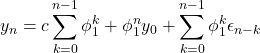
(3) 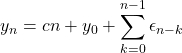
式(3)は、![]() についての1次関数(傾き
についての1次関数(傾き![]() )にノイズが付加された式である。これが図2の上右図に相当する。また、式(2)の右辺にある3つの項全てに
)にノイズが付加された式である。これが図2の上右図に相当する。また、式(2)の右辺にある3つの項全てに![]() の累乗の項が含まれているので、
の累乗の項が含まれているので、![]() のとき、
のとき、![]() が大きいと指数関数的に増大する。これが図2の
が大きいと指数関数的に増大する。これが図2の![]() のグラフが指数関数となる理由である(図では
のグラフが指数関数となる理由である(図では![]() とした)。
とした)。![]() のときグラフは単調増加あるいは指数関数的に増加するから、
のときグラフは単調増加あるいは指数関数的に増加するから、![]() の期待値は時間に依存する。よって
の期待値は時間に依存する。よって![]() のときAR(1)過程は非定常である。
のときAR(1)過程は非定常である。
次に、AR(1)過程の定常性について考える。定常性の定義は以下であった。
![]()
ただし、![]() と
と![]() は時間に依存しない量である。
は時間に依存しない量である。
すなわち、期待値と分散がともに時刻に依存しない場合を定常と呼ぶのであった。MA過程はホワイトノイズの線形結合であったから常に定常性を満たしていたが、AR過程の場合は、ある条件を満たす場合だけ定常となる。AR(1)過程が定常となる条件は以下である。
![]()
この方程式は容易に解けて
![]()
となる。従って、![]() であれば
であれば![]() となり定常となる。
となり定常となる。![]() なら
なら![]() となり非定常となる。定常な場合と非定常な場合のグラフの違いを、図1と図2を見て再度確認してほしい(非定常な場合、グラフは1次関数か指数関数となる)。さて、定常な場合のAR(1)過程の期待値を求める。
となり非定常となる。定常な場合と非定常な場合のグラフの違いを、図1と図2を見て再度確認してほしい(非定常な場合、グラフは1次関数か指数関数となる)。さて、定常な場合のAR(1)過程の期待値を求める。
![]()
定常な場合、![]() であるから
であるから
![]()
(4) ![]()
を得る。図1の4つのグラフでは![]() であったからこれを上式に代入すると
であったからこれを上式に代入すると![]() を得る。図1のグラフは確かに0近傍を振動していることを確認できる。一方、図2の上左図では
を得る。図1のグラフは確かに0近傍を振動していることを確認できる。一方、図2の上左図では![]() であった。これらを上式に代入すると
であった。これらを上式に代入すると![]() である。図2の上左図を見ると確かに10近傍を振動していることが分かる。そして、
である。図2の上左図を見ると確かに10近傍を振動していることが分かる。そして、![]() を1に使づけていくと式(4)より
を1に使づけていくと式(4)より![]() は発散するが、その振る舞いはグラフの指数関数的増大を意味している。次に自己共分散
は発散するが、その振る舞いはグラフの指数関数的増大を意味している。次に自己共分散![]() を求める(
を求める(![]() )。
)。
![Rendered by QuickLaTeX.com \begin{align*} \gamma_k &={\rm Cov}[y_t,y_{t-k}]\\ &={\rm Cov}[c+\phi_1y_{t-1}+\epsilon_t,y_{t-k}]\\ &={\rm Cov}[\phi_1y_{t-1}+\epsilon_t,y_{t-k}]\\ &={\rm Cov}[\phi_1y_{t-1},y_{t-k}]+{\rm Cov}[\epsilon_t,y_{t-k}]\\ &={\rm Cov}[\phi_1y_{t-1},y_{t-k}]\\ &=\phi_1{\rm Cov}[y_{t-1},y_{t-k}]\\ &=\phi_1{\rm Cov}[y_{t-1},y_{t-1-(k-1)}]\\ &=\phi_1\gamma_{k-1} \end{align*}](/wp-content/ql-cache/quicklatex.com-1573bb52f6abb0f6a47aadabe796af12_l3.png)
![]() のときは次式となる。
のときは次式となる。
![Rendered by QuickLaTeX.com \begin{align*} \gamma_0 &={\rm Cov}[y_t,y_{t}]\\ &={\rm Cov}[c+\phi_1y_{t-1}+\epsilon_t,c+\phi_1y_{t-1}+\epsilon_t]\\ &={\rm Cov}[\phi_1y_{t-1},\phi_1y_{t-1}]+{\rm Cov}[\epsilon_t,\epsilon_t]\\ &=\phi_1^2{\rm Cov}[y_{t-1},y_{t-1}]+\sigma^2\\ &=\phi_1^2\gamma_0+\sigma^2 \end{align*}](/wp-content/ql-cache/quicklatex.com-1aad50bd69a22f97d7daebf6dce04c03_l3.png)
これを解いて
![]()
を得る。以上より自己相関![]() は次式で計算される。
は次式で計算される。
![]()
これは等比級数の漸化式なので![]() を厳密に求めることができる。
を厳密に求めることができる。
![]()
![]() なので、
なので、![]() となる。
となる。![]() を増やしていくと、
を増やしていくと、![]() のとき(定常のとき)自己相関は指数関数的に減衰し、
のとき(定常のとき)自己相関は指数関数的に減衰し、![]() のとき(非定常のとき)指数関数的に増大し、
のとき(非定常のとき)指数関数的に増大し、![]() のとき(非定常のとき)
のとき(非定常のとき)![]() のままとなる。ここで大切なことは、AR過程が定常過程の場合、その自己相関は指数関数的に減衰するということである。
のままとなる。ここで大切なことは、AR過程が定常過程の場合、その自己相関は指数関数的に減衰するということである。
最後に、AR過程とMA過程の関係について一言ふれておく。![]() のとき(定常のとき)、
のとき(定常のとき)、![]() で式(2)は
で式(2)は
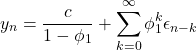
となる。これはホワイトノイズの線形和であり、前回説明したMA過程に相当する。すなわち、AR(1)過程が定常な場合(![]() )、AR(1)過程はMA(
)、AR(1)過程はMA(![]() )過程と等価になる。
)過程と等価になる。
さて、AR(1)過程を一般化したAR(![]() )過程を与える式は次式になる。
)過程を与える式は次式になる。
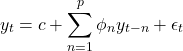
これについての議論は煩雑になるので今回は取り上げない。興味があれば下に挙げた参考文献を見てほしい。
AR過程の長所と短所
AR過程の長所と短所を以下にまとめる。
長所
- 過去のデータに基づく予測が可能である(自己回帰的)。
- 長期に渡る相関を少ないパラメータ数で表現できる。
- 周期性(季節性)を取り込むことができる。
- モデルが単純で理解しやすい。
- パラメータの数が少ないため計算コストが低い。
短所
- 自己相関なので外れ値の影響がしばらく続く。ただし、定常過程の場合は自己相関は指数関数的に減衰するのでいずれ影響はなくなる。
- 過去のデータを利用できない場合に適用が難しい。
まとめ
今回は、AR過程の最も簡単な場合(AR(1)過程)について説明した。MA過程は常に定常となるが、AR過程ではある条件下でのみ定常となる。AR(1)過程の場合は、![]() の場合に定常となり、そのときの自己相関
の場合に定常となり、そのときの自己相関![]() は、
は、![]() が大きくなると(現在の時刻から離れると)、指数関数的に減衰することを見た。また、定常な場合は、AR(1)過程はMA(
が大きくなると(現在の時刻から離れると)、指数関数的に減衰することを見た。また、定常な場合は、AR(1)過程はMA(![]() )過程に帰着することも示した。一方、
)過程に帰着することも示した。一方、![]() の場合(非定常な場合)、
の場合(非定常な場合)、![]() のグラフは指数関数的に増大することも示した。
のグラフは指数関数的に増大することも示した。
参考文献

