毎月アルゴリズム – 第1回 –

はじめに

こんにちは。よっしーです。
先日、初歩的な数学のアルゴリズムを考えてみようというブログを書かせていただきました。
アルゴリズムはあまり詳しくなかったので調べながら書いていたのですが、思ったよりも面白くてもうちょっと勉強
してみようかなと思い、毎月少しずつアルゴリズム記事を書いていこうと思い立ちました。
今回がその一回目です(前回のものは第0回ということで笑)。
自分も勉強中ですので、拙い文章や表現がわかりにくいところがあるかもしれませんがご容赦ください。
良ければ毎月見てくださいますと幸いです。

アルゴリズムとは

アルゴリズムとは特定の手順を追って実行すれば解を得ることができるor解がない場合はそのことが確かめられる手順のことを指します。
なので、プログラムを組むということは特定のアルゴリズムを実行しているにすぎません。

アルゴリズムはよく料理の下準備や、レシピに例えられます。
ニンジンをいちょう切りにするための切り方でも効率よく切れば、包丁を動かす回数を減らしながら、同じ結果を得ることができます。
おいしいシチューのレシピは一度作ってしまうと、今後それをトレースするだけでずっと同じおいしいシチューを作り続けることができます。

プログラミングにおいても同じことが言えます。
同じ結果になるプログラムを書いてくれと100人依頼すれば100通りのコードができます。
100通りのアルゴリズムがある中で、良いもの、悪いものに分かれたりするのですが、一般的にプログラミングの界隈では計算効率が良いものを良いアルゴリズムと言います。
過去のプログラマーが効率の良いアルゴリズムを考えてくれているのでそのアルゴリズムをいくつか紹介していけたら良いなと思います。

アルゴリズムを考える前に

計算量ってどうやって変わるの？

少し下準備として計算量の話をしておきます。
計算量を考えるときはアルゴリズムで実行する計算の試行回数が何に比例するか考えることが重要です。
ただ厳密に何に比例するかを考えるのではなく、一番計算量に大きく関わると考えられる項を考えます。

以下のようなコードを考えてみます。

// case1

var num = 10;

for (var i = 0; i < num; i++)
{
    // 計算
}

// case1

var num = 10;

for (var i = 0; i < num; i++)

{

// 計算

}

// case2
var num = 10;

for (var i = 0; i < num; i++)
{
    for (var j = 0; j < num; j++)
    {
        // 計算
    }
}

// case2

var num = 10;

for (var i = 0; i < num; i++)

{

for (var j = 0; j < num; j++)

{

// 計算

}

上記2つのfor文を回したときに計算にかかる時間はどのくらい変わるでしょうか？
ここでは単純にループの回数=計算にかかる時間と考えてよいです。
case1は10回ループが回って、case2は100回ループが回ります。
ここで、上でおいた変数numはデータ数とかで変わったりしますので仮に10,000になったとしたらどうなるでしょう。

case1: 10,000 回
case2: 100,000,000 回

桁数が大きく離れてしまいました。
一般的に考えると、case1は $n$ に比例し、case2は $n^2$ に比例しています。
両者の計算量はデータの個数が増えるだけでとても大きな差ができてしまいます。

オーダーの話

上記で $n$ と $n^2$ では大きな違いがあるという話をしました。
数が大きくなれば $n^2$ の計算に比べて $n$ という数字はどんどん小さくなっていきます。
それは2数を比べる際だけではなく、同じ式の中でも同様です。
case2において $n^2$ 回ループが回るという話をしましたが、ループはそんなきれいに $n^2$ 回計算されるとかにはならないことが多いです。
例えば $2n^2+3n+4$ 回回るとか、何かしらの式で表されるような回数の計算が行われたりします。
前と同じように $n$ に10,000を入れてみたらどうなるでしょうか。

$2n^2 + 3n + 4 = 200,030,004$

$3n + 4$ が寄与している部分はとても小さいことがわかります。
なら、大体 $2n^2 + 3n + 4$ は $2n^2$ と同じでいいよねってなりませんか？
アルゴリズムの計算量においては変化の度合いが一番大きいもの以外は無視します。
今回だと $2n^2$ が一番変化の度合いが大きいので $3n + 4$ は無視してしまいます。

今度は $2n^2$ と $n^2$ の違いに関してです。
$2n^2$ と $n^2$ と $2n$ を考えて、上記と同様に $n$ に10,000を入れたときのことを考えます。

$2n^2 = 200,000,000$
$n^2 = 100,000,000$
$2n = 20,000$

次に $n$ に20,000を入れてみると

$2n^2 = 800,000,000$
$n^2 = 400,000,000$
$2n = 40,000$

$2n^2$ と $n^2$ を比べたとき、 $n$ にどんな値を入れようとも2倍しか差は出ません(係数ってそういうものなので)。
でも $2n^2$ と $2n$ を比べたとき、 $n$ に入れた値を変えるだけで数値が相当大きく動くことがわかります。
$2n^2$ において、数の変化の影響を最も受けるのは $n$ だということがわかります。
そのため、計算量に最も関わるのは $n$ の部分なんだなと言うことがわかりますので、大雑把に計算量を見積もるときは係数は無視していいよねってなりませんか？
アルゴリズムの計算量においては係数部分は無視することになります。

上を整理し、計算量を表す記号を導入すると、

最高次数の項以外は無視できる(一番計算量の寄与が大きい項以外無視できる)
$2n^2 + 3n + 4 \to 2n^2$
係数は無視できる
$2n^2 \to n^2$
それをアルゴリズムの計算量オーダーと呼び、ランダウ記号で以下のように表す。
$O(n^2)$

よく出てくるオーダー

計算量として、 $n$ や $n^2$ というのが出てきましたが、アルゴリズムを勉強しているとしばしば以下のオーダーに出会うことになります。
$O(\log n)$ , $O(n)$ , $O(n\log n)$ , $O(n^2)$ , $O(2^n)$ , $O(n!)$

計算量は以下のようになります。
$O(\log n) < O(n) < O(n\log n) < O(n^2) < O(2^n) < O(n!)$

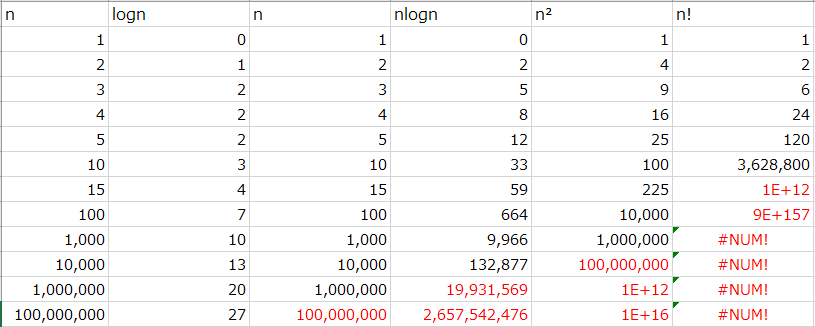
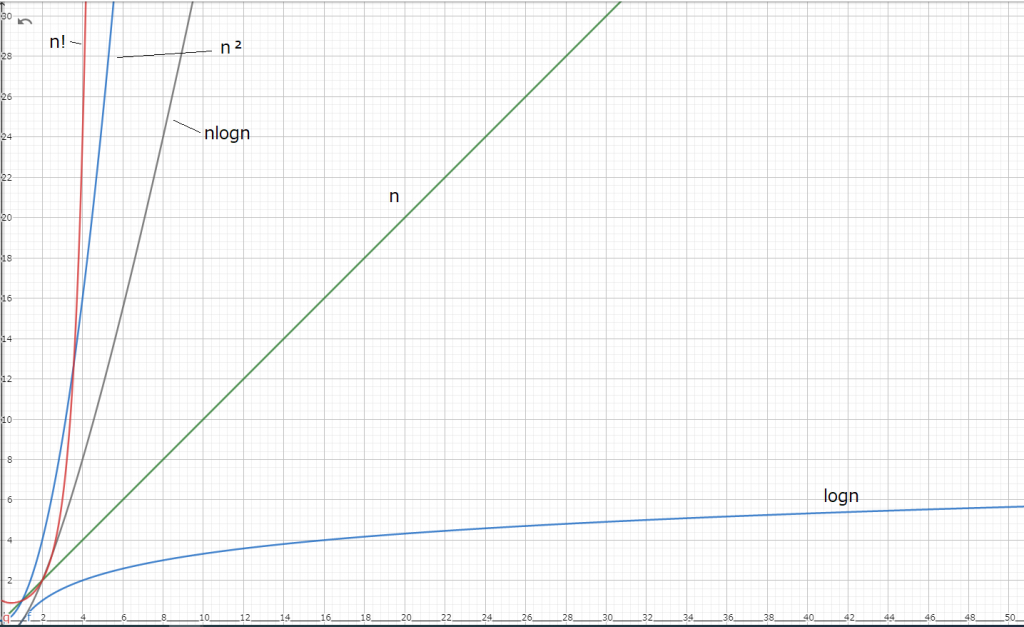
ループ数でどのように計算量が推移するか表とグラフにまとめてみました。
$10^8$ を超えるデータは赤字にしています。
$n!$ は急速な勢いで伸びてることがわかります( $10^300$ 程度より大きくなるとExcelの仕様上#NUM!と表示されてしまいます)。
逆に $\log n$ はとても緩やかに増加することがわかります。

アルゴリズムを考えてみる

アルゴリズムの代表的なものとしてソートがあります。
ソートとは特定の規則に従ってデータを並び替えることです。
並び替えかたにもいろいろなアルゴリズムがあるので今回は一つだけ紹介します。

バブルソート

概要

バブルソートは隣接する2つの数字を比較して入れ替える操作を繰り返してソートを行う手法です。
どんどん左に数字が移動していく様子(大きい数字が少しずつ右に行く)が泡のようだからついたと言われています。

オーダー

オーダーは $O(n^2)$ です。
試行回数の計算は
$(n-1) + (n-2) + (n-3) + ...... + 3 + 2 + 1 = n(n-1)/2$ 回となります。
この回数はデータによらず一定になります(後で処理内容を説明すると自明になります)。

処理

元データを用意する
データ列の一番右のデータ(以下A)とその一つ左隣のデータ(以下B)を比較する
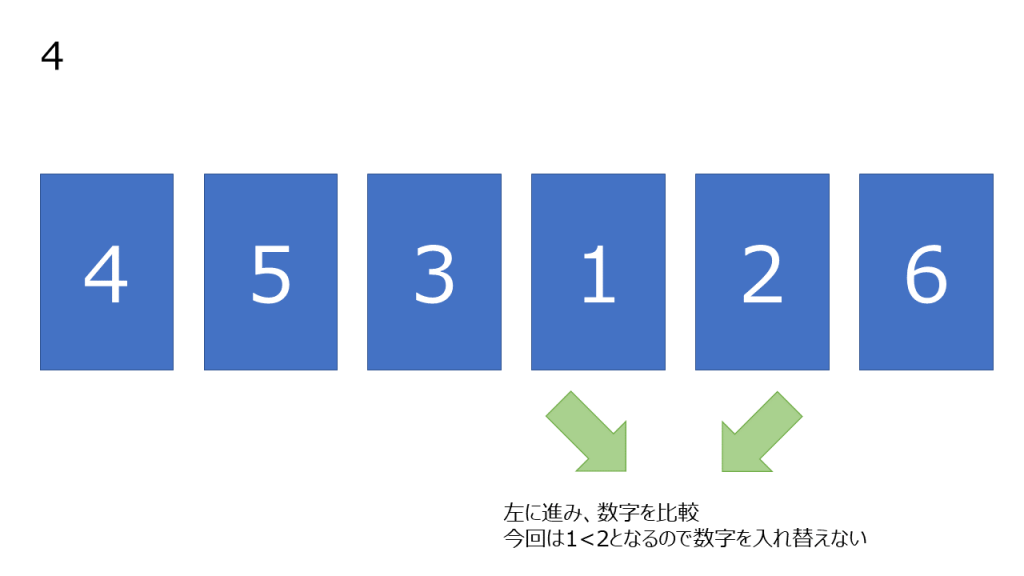
A < B となる場合数字を入れ替える(それ以外の場合はそのまま)
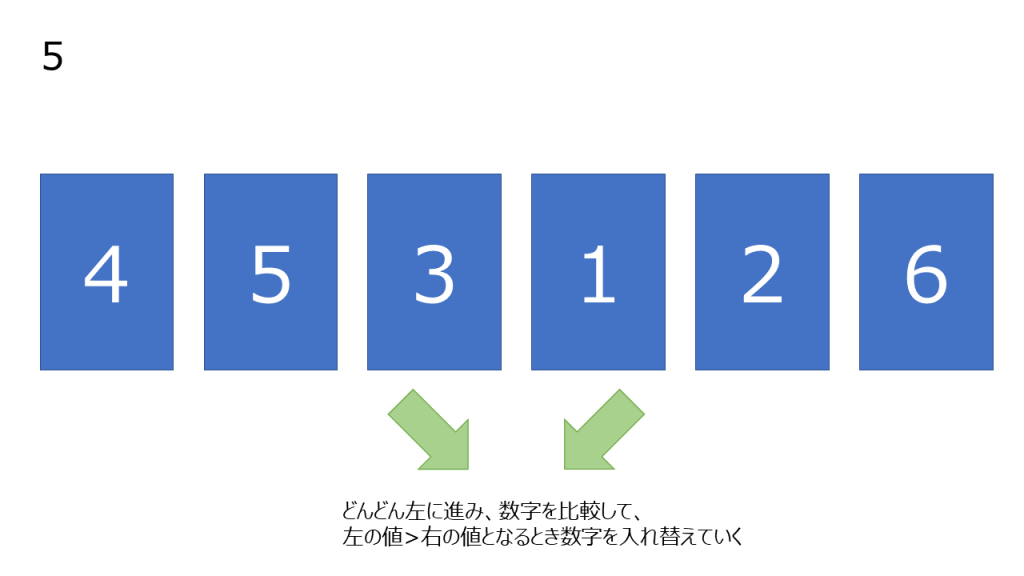
要素を一つ左にずらし、右から2番目のデータと右から三番目のデータ(以下C)を比較する
B < C となる場合数字を入れ替える(それ以外の場合はそのまま)
4, 5 の処理を繰り返し行い(比較する要素を一つ左にずらす)、ソート済みのデータの前まで(今回は1週目なので一番左に行くまで)実行する
一番左の要素をソート済みとする(ここまでで1ラウンド)
2 ~ 7 の操作を繰り返し、すべてがソート済みのデータになるまで行う

上記処理の簡略図

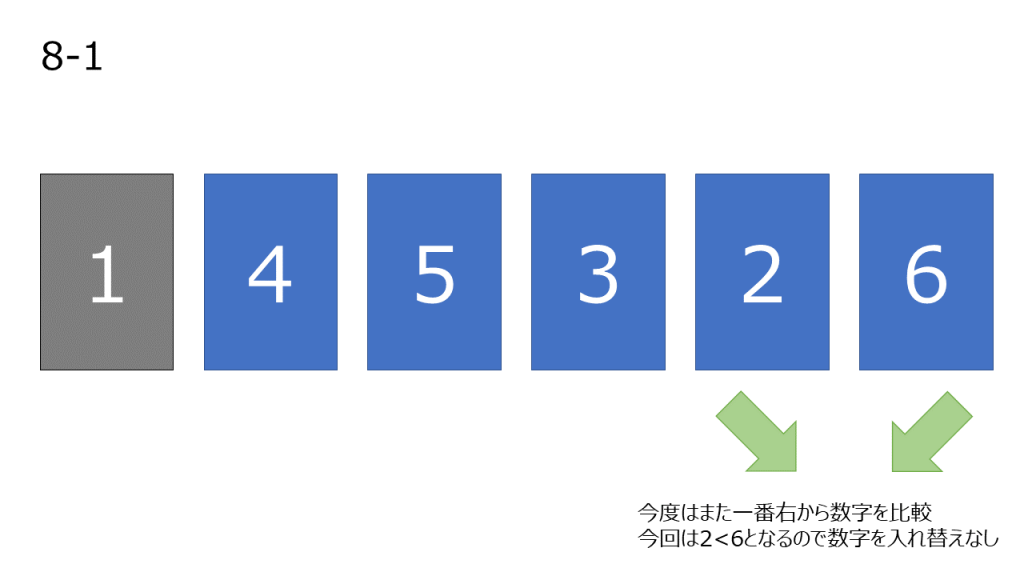
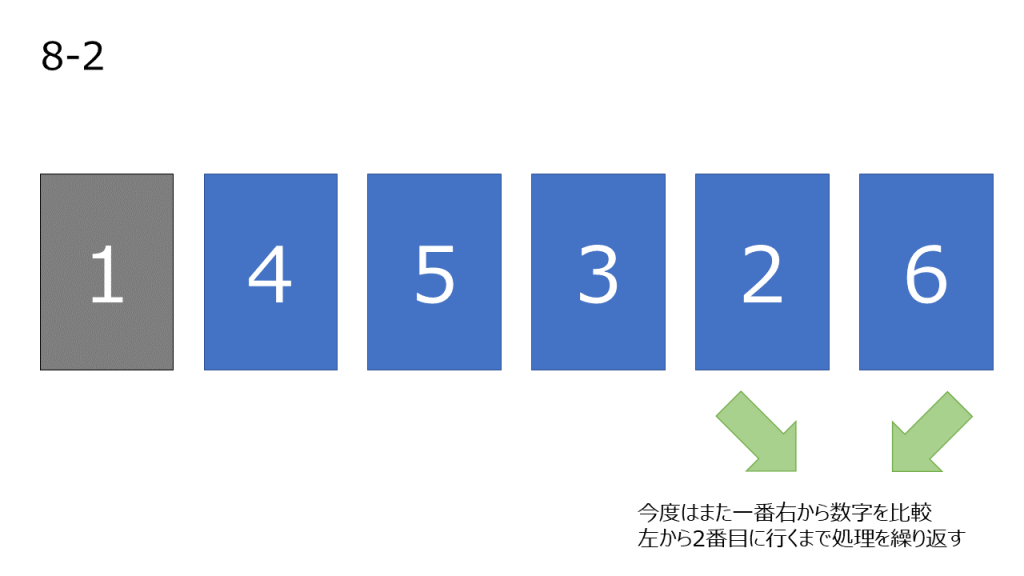
コード

上記バブルソートのコードを考えてみました。
コードはC#で書いています。

using System;
using System.Collections.Generic;
using System.Linq;

namespace Algorithm
{
  class Program
  {
    static void Main(string[] args)
    {
      var list = new List<int>();
      
      // 1～20の数字をバラバラに配列に入れる
      for (var i = 1; i < 21; i++)
      {
        list.Add(i);
      }

      var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

      Console.WriteLine("{" + string.Join(",", array) + "}");

      Console.WriteLine("{" + string.Join(",", BubbleSort(array)) + "}");
    }

    private static int[] BubbleSort(int[] arr)
    {
      for (var i = 0; i < arr.Length; i++)
      {
        // 右から隣り合わせになった数値を比較して入れ替える
        // ソート済みの数字には触れないようにする
        for (var sort = arr.Length - 1; sort > i; sort--)
        {
          if (arr[sort] < arr[sort - 1])
          {
            var tmp = arr[sort];
            arr[sort] = arr[sort - 1];
            arr[sort - 1] = tmp;
          }
        }
      }

      return arr;
    }
  }
}

using System;

using System.Collections.Generic;

using System.Linq;

namespace Algorithm

{

class Program

{

static void Main(string[] args)

{

var list = new List<int>();

// 1～20の数字をバラバラに配列に入れる

for (var i = 1; i < 21; i++)

{

list.Add(i);

}

var array = list.OrderBy(x => Guid.NewGuid()).ToArray();

Console.WriteLine("{" + string.Join(",", array) + "}");

Console.WriteLine("{" + string.Join(",", BubbleSort(array)) + "}");

}

private static int[] BubbleSort(int[] arr)

{

for (var i = 0; i < arr.Length; i++)

{

// 右から隣り合わせになった数値を比較して入れ替える

// ソート済みの数字には触れないようにする

for (var sort = arr.Length - 1; sort > i; sort--)

{

if (arr[sort] < arr[sort - 1])

{

var tmp = arr[sort];

arr[sort] = arr[sort - 1];

arr[sort - 1] = tmp;

}

return arr;

}

終わりに

今回は簡単なオーダーの説明と、実際にソートのアルゴリズムを一つ考えてみました。
今後も少しずつアルゴリズムを考えてブログに残していけたらなと思いますので、見ていただけますと幸いです。

Blazor WebAssembly で MVVM を実現する(第1回)

Conditional Variational Autoencoder

毎月アルゴリズム – 第1回 –

はじめに

アルゴリズムとは

アルゴリズムを考える前に

計算量ってどうやって変わるの？

オーダーの話

よく出てくるオーダー

アルゴリズムを考えてみる

バブルソート

概要

オーダー

処理

上記処理の簡略図

コード

終わりに

最近の記事

レイアウト解析

ChatGPTを用いた画像異常検知

クォータニオンと回転行列の関係

OpenCVで深層学習

OpenCVのcv::Matに関する小ネタ集

テンソルネットワークの入り口（その2）

初歩的な数学のアルゴリズムを考えてみよう

毎月アルゴリズム – 第7回 –

毎月アルゴリズム – 第5回 –

毎月アルゴリズム – 第3回 –

毎月アルゴリズム – 第6回 –

【モンテカルロ法】プログラミングで円周率を求める方法

Google Vision APIでOCR

アーカイブ

カテゴリー