はじめに
こんにちは。よっしーです。
毎月アルゴリズムを考えていくブログの第 7 回目です。
前回から少し期間が空いてしまい申し訳ありません。(毎月アルゴリズムではなくなってしまう!笑)
前回に引き続き今回も探索に関するアルゴリズムを考えています。
今回も探索のアルゴリズムを 1 つ紹介して、探索のアルゴリズムを終えようかと思います。
良ければ御覧ください。
アルゴリズムを考えてみる
本日は以下の探索に関してアルゴリズムを考えていきます。
今回は探索アルゴリズムの分類としては 1 つなんですが、衝突が起こった場合に破綻しないためのロジックが 2 種類ほど方法論としてあるのでそちらを紹介します。
- ハッシュ探索
- チェイン法(分離連鎖法)
- オープンアドレス法
ハッシュ探索
概要
以前紹介したデータ構造のハッシュテーブルの考え方を用いて、収納されたデータを取り出す方法です。
詳しい原理は 第2回で解説しているので省略しますが、データをハッシュ関数を用いてハッシュテーブル格納し、同じハッシュ関数をかけて探索値をハッシュテーブルから高速で探し出す探索方法です。
オーダー
ハッシュ値を用いてデータの挿入、探索を行うため、 ![]() です。
です。
ハッシュ値の衝突
ハッシュ関数は一定のアルゴリズムで同じ Key から必ず同じ数値が返ってくるメソッドということを以前お伝えしたと思います。
ただし、別の Key でも同じ数値が返ってくることがあります。
これをハッシュ値の衝突と言います。
とても単純なロジックで考えてみましょう。
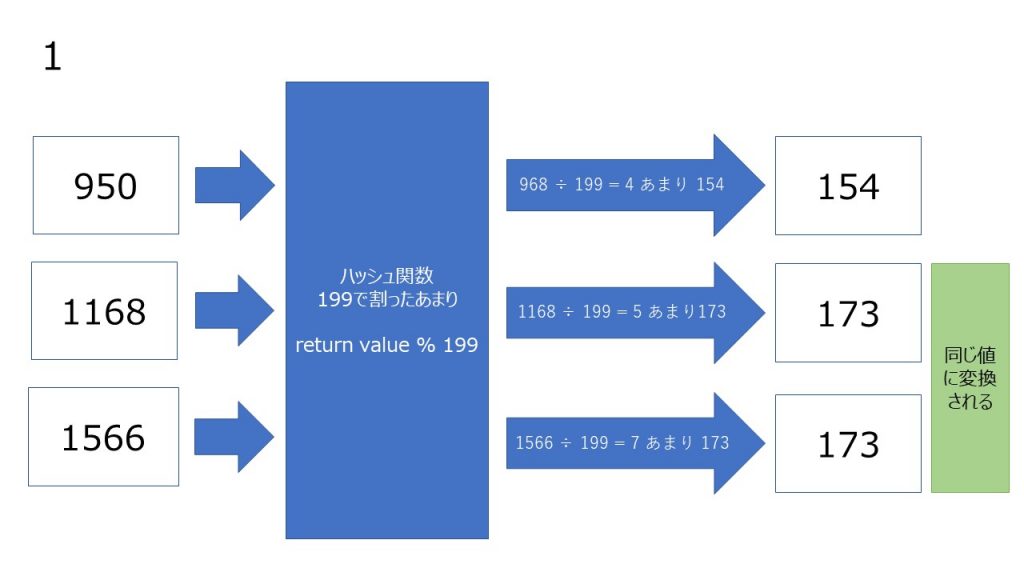
できるだけ衝突を起こしにくい関数を作るために日夜アルゴリズムは考えられていますが、衝突は起こってしまうものとして、衝突が起こったときの処理を考えておく必要があります。
その代表的な方法は以下です。
- チェイン法(分離連鎖法)
- オープンアドレス法
チェイン法(分離連鎖法)
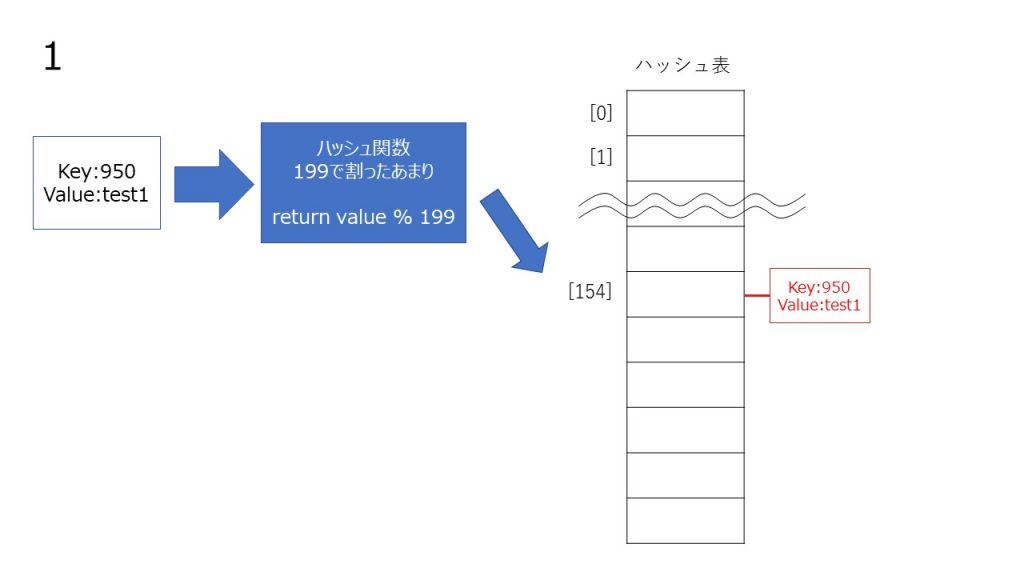
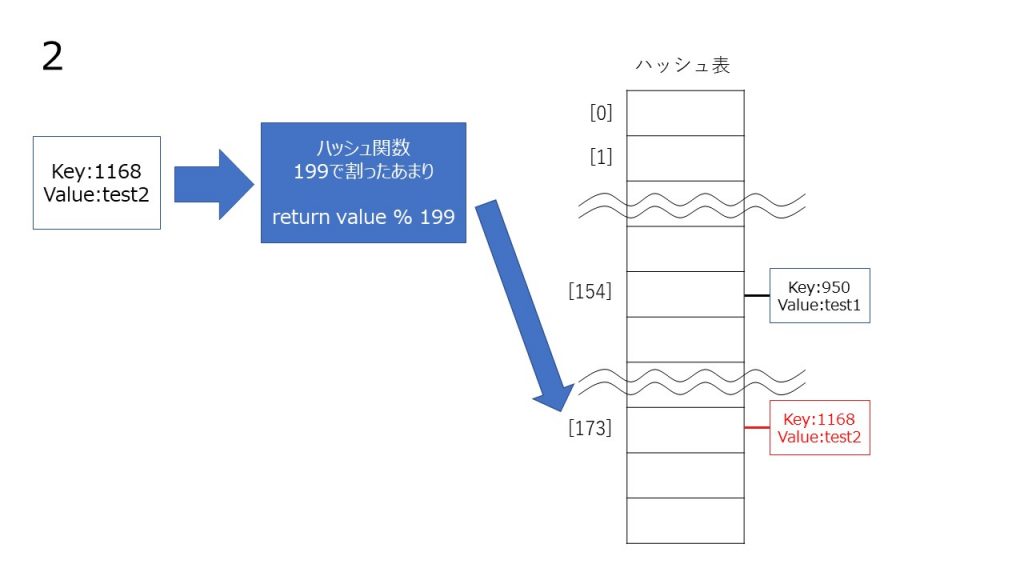
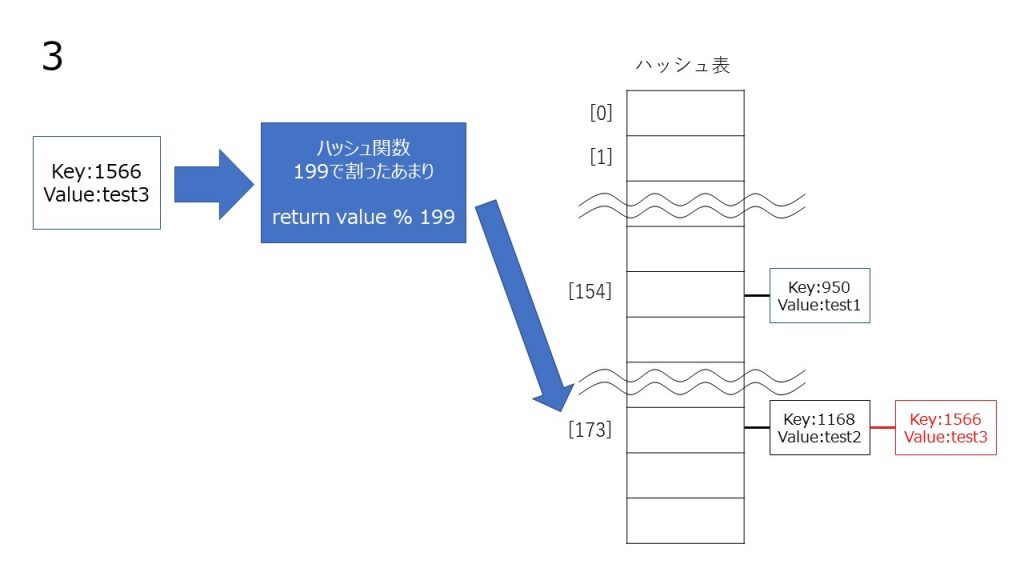
チェイン法は、同じハッシュ値のデータを連結リストでつなげていくことによって衝突を起こしても同じハッシュ値に複数データを格納することによって回避する方法です。
線形のリストに格納する性質上、線形リストが長くなると検索効率が落ちるので、できるだけハッシュ値が衝突を起こさないように、ハッシュ関数を考える必要があります。
コード
チェイン法を用いたハッシュ検索を行える構造を C#で書いてみました。
構造的な部分を重視したので、ハッシュ関数の作成、より効率のいい設計を目指すことは省きました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 |
using System; using System.Collections.Generic; using System.Security.Cryptography; using System.Text; namespace Algorithm.Search { public class ChainHash { public class Node { // 何番目のNodeか public int Number { get; set; } // キー public string Key { get; set; } // 値 public string Value { get; set; } // 次の要素 public Node Next { get; set; } } // 初期データから、mapのサイズを決定する private readonly int capacity; // Nodeのmap。ハッシュ値から添え字を計算して、はじめのデータを格納していく private readonly Node[] map; // 全データ数 private int count = 1; public ChainHash() { this.capacity = 1103; // 1000程度の素数としておく this.map = new Node[this.capacity]; } private uint Pow(int baseNum, int exponentNum) { uint result = 1; for (var i = 0; i < exponentNum; i++) { result *= (uint)baseNum; } return result; } // Hash関数 private int GetHashCode(string key) { // String.GetHashCode()は文字列が同じの場合同じHashCodeを返すわけではないので、MD5のHash関数を用いる var tmpSource = Encoding.ASCII.GetBytes(key); ; var tmpHash = new MD5CryptoServiceProvider().ComputeHash(tmpSource); uint sum = 0; // 16byte長で返却されるので、それらを16進数と見立てて数値を生成。かぶりづらくなるはず。 for (var i = 0; i < tmpHash.Length; i++) { sum += this.Pow(tmpHash[i], 16 - i); } var result = sum % this.capacity; // intのcapacityで割ったあまりのためintの範囲に収まる return (int)result; } // Hashテーブルに要素を追加する関数 public void Add(string addKey, string value) { var key = this.GetHashCode(addKey); if (addKey == null) { throw new ArgumentNullException("nullをKeyにできません"); } var node = this.map[key]; var addNode = new Node() { Number = this.count, Key = addKey, Value = value }; // そもそもMapにないならMapに含める if (node == null) { this.map[key] = addNode; this.count++; return; } while (node.Next != null) { // すでに登録されているものは登録しない if (node.Key == addKey) { throw new ArgumentException("Keyが重複しています"); } node = node.Next; } node.Next = addNode; this.count++; } // Hashテーブルの要素を削除する関数 public void Remove(string removeKey) { var key = this.GetHashCode(removeKey); var node = this.map[key]; // ない場合は離脱 if (node == null) { return; } var isExist = false; var num = 0; if (node.Key == removeKey) { // 先頭を削除する場合 num = node.Number; this.map[key] = node?.Next ?? null; isExist = true; } else { // nextの参照を変更する var old = node; while (node != null) { if (node.Key == removeKey) { num = node.Number; old.Next = node.Next ?? null; isExist = true; break; } old = node; node = node.Next; } } if (!isExist) { return; } this.count--; // 微妙な実装だが、全走査してnumberをデクリメントする if (num == 0) { return; } foreach (var item in this.map) { var n = item; while (n != null) { if (n.Number > num) { n.Number--; } n = n.Next; } } } // Hashテーブルに存在するNodeを検索する関数 public Node Search(string target) { var key = this.GetHashCode(target); var node = this.map[key]; // ない場合は離脱 if (node == null) { return null; } if (node.Key == target) { return node; } else { while (node != null) { if (node.Key == target) { return node; } node = node.Next; } } return null; } } } |
オープンアドレス法
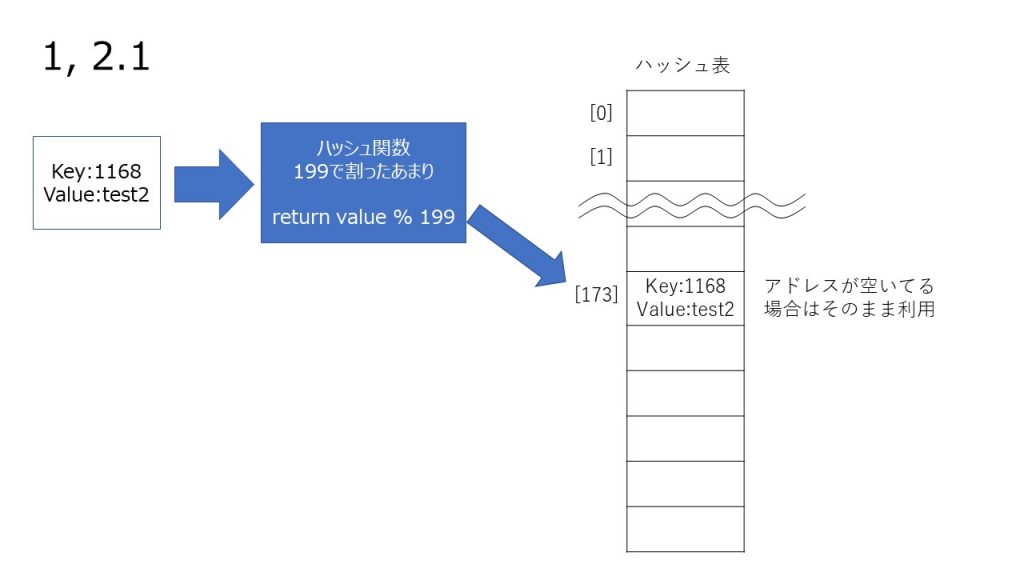
オープンアドレス法は格納したい値からハッシュ値を計算し、そこからアドレスを計算して配列に格納するというところまではチェイン法と同じです。
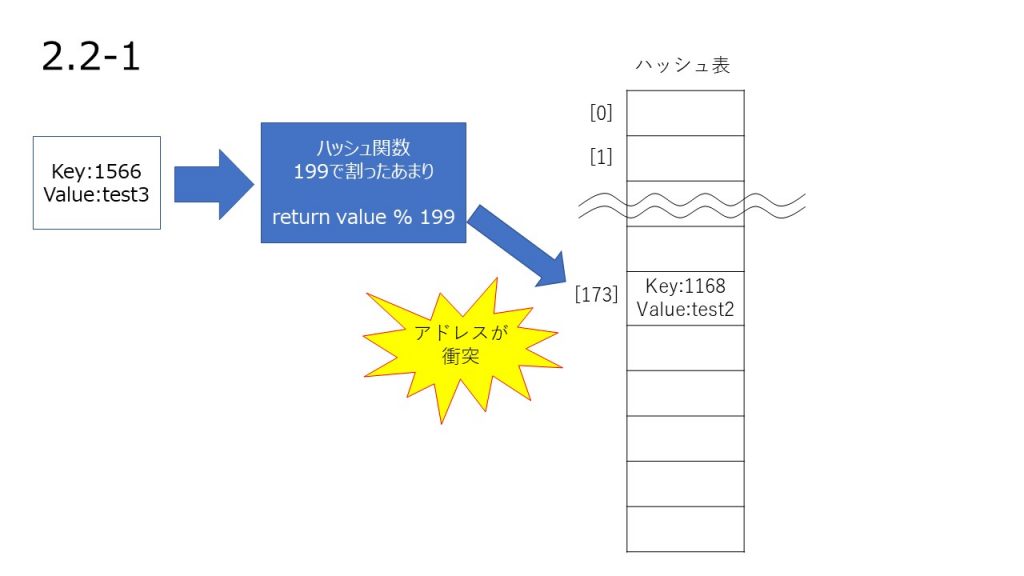
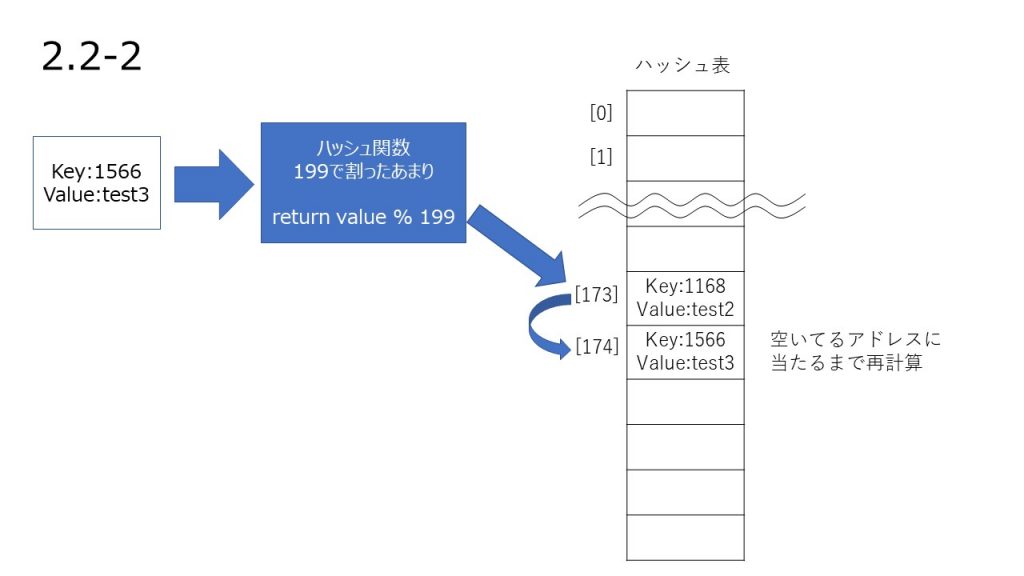
アドレスが衝突していたとき、アドレスを再計算して別のアドレスに格納する処理を行います。
上記で別のアドレスにも値が格納されていた場合、別のアドレスを再計算し、そのアドレスに格納するという処理を繰り返し行います。
処理
最も単純に処理を書くとすると以下になります
- 格納するデータよりインデックスの計算(アドレス作成)
- 計算したアドレスが衝突しているか
- Yes の場合:アドレスを再計算 2 に戻る
- No の場合:値を格納する-> end
アドレスの計算ロジックは工夫しなければ、埋まっているアドレスが多くなってきた場合に性能が劣化してしまいます。
今回はハッシュの再計算のロジックは簡単なものとして、線形走査法、二重ハッシュ法というものがあるのでそれも紹介しておきます。
ハッシュの再計算
あるハッシュ関数 ![]() を定義したとして、引数
を定義したとして、引数 ![]() を取ったとき、それにより得られるハッシュ値を
を取ったとき、それにより得られるハッシュ値を![]() と定義します。
と定義します。
![]() はあるハッシュ値で数値を取るものとします。
はあるハッシュ値で数値を取るものとします。
線形走査法
あるハッシュ関数 ![]() において、線形走査法におけるハッシュ値は以下で記されます。
において、線形走査法におけるハッシュ値は以下で記されます。
ハッシュの配列の大きさを M とし、k 回目の再ハッシュ関数は以下で定義される。
![]()
一見難しく記載していますが、前述のコードで利用しているハッシュ関数は以下です。
![]()
これに 1 ずつ加えていって、M を超えるようなら 0 に戻してくださいねと言ってるのが線形操作法です。
とても噛み砕いて言うとアドレスが埋まっていたら一つ隣のアドレスを使ってくださいということになります。
二重ハッシュ法
あるハッシュ関数![]() を用いて、二重ハッシュ法におけるハッシュ値は以下で記されます。
を用いて、二重ハッシュ法におけるハッシュ値は以下で記されます。
ハッシュの配列の大きさを M とし、k 回目の再ハッシュ関数は以下で定義される。
![]()
線形走査法に形が似ています。
![]() のとき、線形操作法になります。
のとき、線形操作法になります。
ここで、![]() は簡単な関数にしないと再計算に時間がかかってしまいます。
は簡単な関数にしないと再計算に時間がかかってしまいます。
一般的には以下のようにするのが望ましいとされています。
![]()
q は M より小さい値で、この値 ![]() は M と互いに素(※)になっていないとすべてを走査することはできません。
は M と互いに素(※)になっていないとすべてを走査することはできません。
そのため、M は素数を取ることが多くなります。
※ 互いに素とは
2 つの整数が 1 以外の公約数を持たないこと
15 と 27 は素因数分解すると ![]() と公約数を 1 しか持たないため互いに素となる。
と公約数を 1 しか持たないため互いに素となる。
15 と 24 は素因数分解すると ![]() と 3 を公約数に持つので互いに素とならない。
と 3 を公約数に持つので互いに素とならない。
コード
今回は単純化するため線形走査法を用いて、オープンアドレス法を実装したいと思います。
いつもどおり、C#で書いてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 |
using System; using System.Collections.Generic; using System.Linq; using System.Security.Cryptography; using System.Text; namespace Algorithm.Search { public class OpenAddress { private class Node { public string Key { get; set; } public string Value { get; set; } } // 初期データから、mapのサイズを決定する private int capacity; // Nodeのmap。ハッシュ値から添え字を計算して、はじめのデータを格納していく private Node[] map; // 全データ数 private int count = 0; private static readonly int[] s_primes = { 3, 7, 11, 17, 23, 29, 37, 47, 59, 71, 89, 107, 131, 163, 197, 239, 293, 353, 431, 521, 631, 761, 919, 1103, 1327, 1597, 1931, 2333, 2801, 3371, 4049, 4861, 5839, 7013, 8419, 10103, 12143, 14591, 17519, 21023, 25229, 30293, 36353, 43627, 52361, 62851, 75431, 90523, 108631, 130363, 156437, 187751, 225307, 270371, 324449, 389357, 467237, 560689, 672827, 807403, 968897, 1162687, 1395263, 1674319, 2009191, 2411033, 2893249, 3471899, 4166287, 4999559, 5999471, 7199369 }; public OpenAddress() { this.capacity = s_primes[1]; this.map = new Node[this.capacity]; } private uint Pow(int baseNum, int exponentNum) { uint result = 1; for (var i = 0; i < exponentNum; i++) { result *= (uint)baseNum; } return result; } // Hash関数 private int GetHashCode(string key) { // String.GetHashCode()は文字列が同じの場合同じHashCodeを返すわけではないので、MD5のHash関数を用いる var tmpSource = Encoding.ASCII.GetBytes(key); ; var tmpHash = new MD5CryptoServiceProvider().ComputeHash(tmpSource); uint sum = 0; // 16byte長で返却されるので、それらを16進数と見立てて数値を生成。かぶりづらくなるはず。 for (var i = 0; i < tmpHash.Length; i++) { sum += this.Pow(tmpHash[i], 16 - i); } var result = sum % this.capacity; // intのcapacityで割ったあまりのためintの範囲に収まる return (int)result; } private void ScaleUp() { this.capacity = new List<int>(s_primes).Find(x => x > this.capacity); var nodes = new Node[this.capacity]; // 一度カウントをクリアする this.count = 0; // Keyがnullのデータ(削除済みデータ)はここで落とす foreach (var datum in this.map.Where(x => x != null && x.Key != null)) { this.Add(nodes, datum); } this.map = nodes; } private int NewAddress(int address) { return (address + 1) % this.capacity; } private void RecursiveSearchOpenAddress(Node[] nodes, Node newNode, int address) { if (nodes[address] == null) { nodes[address] = newNode; this.count++; return; } else if (nodes[address].Key == newNode.Key) { // Keyが重複している場合は何もしない。 throw new ArgumentException("Keyが重複しています"); } address = NewAddress(address); this.RecursiveSearchOpenAddress(nodes, newNode, address); } public void Add(string key, string value) { if (key == null) { throw new ArgumentNullException("nullをKeyにできません"); } if (this.count >= this.capacity) { // キャパシティより大きくなってしまうとこれ以上追加することはできない。 // キャパシティを増やすロジックが必要となる this.ScaleUp(); } this.Add(this.map, new Node { Key = key, Value = value }); } // Hashテーブルに要素を追加する関数 private void Add(Node[] nodes, Node newNode) { var key = this.GetHashCode(newNode.Key); this.RecursiveSearchOpenAddress(nodes, newNode, key); } private void RecursiveSearchRemoveNode(Node[] nodes, string key, int address) { if (nodes[address] == null) { // Keyが存在しない場合、何もしない return; } else if (nodes[address].Key == key) { // キーのみnullにする nodes[address].Key = null; this.count--; return; } address = NewAddress(address); this.RecursiveSearchRemoveNode(nodes, key, address); } // Hashテーブルの要素を削除する関数 public void Remove(string removeData) { var key = this.GetHashCode(removeData); this.RecursiveSearchRemoveNode(this.map, removeData, key); } private string RecursiveSearch(Node[] nodes, string key, int address) { if (nodes[address] == null) { // Keyが存在しない場合、nullをかえす return null; } else if (nodes[address].Key == key) { return nodes[address].Value; } address = NewAddress(address); return this.RecursiveSearch(nodes, key, address); } // Hashテーブルに存在するNodeを検索する関数 public string Search(string target) { var key = this.GetHashCode(target); return this.RecursiveSearch(this.map, target, key); } } } |
おわりに
今回は 1 つの検索方法なのに内容にボリュームがとてもあったと思います。
でも直感的に理解できるものだとは思いますのでぜひアルゴリズムの参考にしていただけたらと思います!
■ 序章
第0回 (初歩的な数学のアルゴリズムを考えてみよう)
■ ソートのアルゴリズム
第1回
第2回
第3回
第4回
第5回
■ 検索のアルゴリズム
第6回

