はじめに
こんにちは。よっしーです。
毎月アルゴリズムを考えていくブログの第3回目です。
前回はデータ構造に関して考えた後にソートのアルゴリズムを紹介しました。
データ構造の話が大半を占めており、メインがデータ構造のブログになってしまいました。笑
アルゴリズムを考える上で、データ構造は重要なものですので、避けて通れないので力を入れてお話しました。
今回もデータ構造に関して少しお話してその後、アルゴリズムを紹介したいと思います。
それでは早速考えていきましょう。
今回もアルゴリズムを考える前に
データ構造を考えよう その2
前回同様データ構造に関してお話したいと思います。
今回はスタック、キューに関して解説します。
前回と同様にデータ構造は文章での説明より図の説明のほうが分かりやすいので、少し図が多くなってしまいます。
退屈かもしれませんが見ていただけますと幸いです。
スタック
スタックはデータを一列に並べるのですが、最後に追加したデータからしか取り出せないという特徴があります。
よく、積み上げられた本に例えられることが多いです。
新しい本を本の上に積みますが、真ん中の本を取りたいときは一番上の本からどけていかないと取れないと言うケースに似ています。
後から入れたものを先に出す、「後入れ先出し」の仕組みを「Last In First Out」、略して「LIFO」と呼びます。
なんかかっこいいですね笑
積み上げていく操作をpushと呼び、要素を取り出す操作をpopと呼びます。
また、リストの先頭をtop、終端をbottomと呼びます。
追加、削除は以下のようになります。
追加
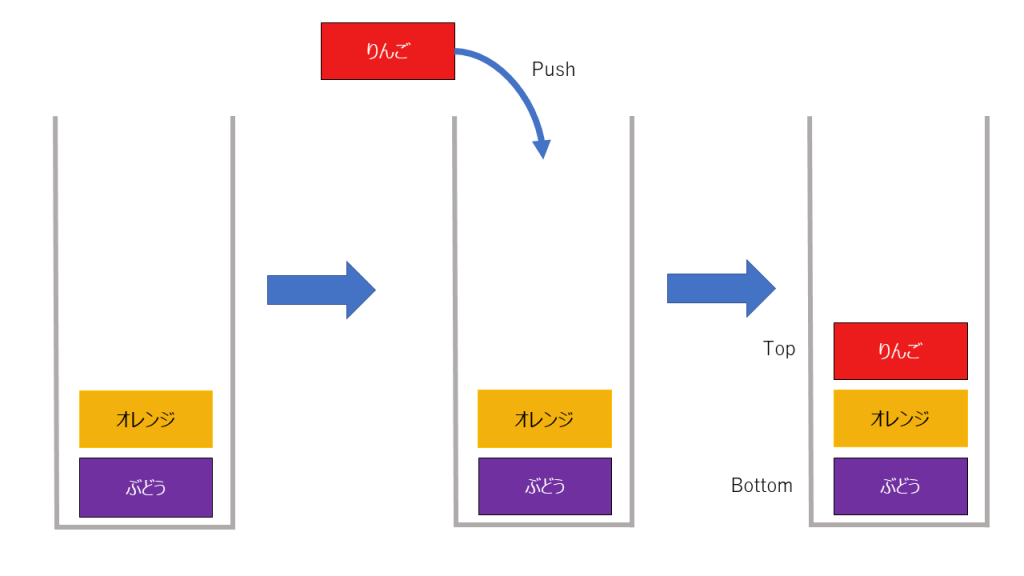
削除
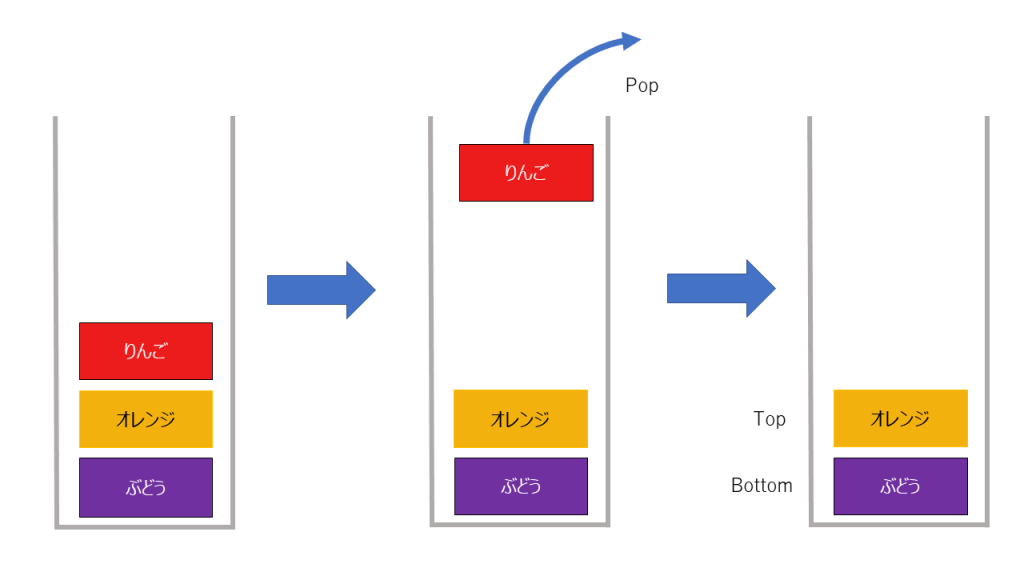
一見すると使いづらいなと思われるこのデータ構造ですが以下の利点があります。
- スタックの実装によるが、一般的に、スタックトップのインデックスあるいはポインタ(スタックポインタと呼ぶ)を増減するだけで、配列内のデータを移動する必要はなく、高速に処理できる
- 利用者はpush, popのみしか操作をすることがないので、利用時のデータの中身がどうとか考えずに操作が可能(制約があることで操作が容易になる)
利用例としてはなにかの履歴に使われることがあります。
例えば、Webブラウザの遷移履歴等を積んでおくことができます。
また、テキストエディタで操作コマンドをスタックに積んでおくことでUndo機能を実装できたりすることができます。
まとめ
- スタックはデータを一列に並べ、先頭にデータを追加していくデータ構造
- データへのアクセスはリストの先頭にのみ制限されている(追加も削除も)
- データの追加、削除するスピードは速い(push, popともにオーダーは
 )
)
キュー
キューはスタックと同様にデータを一列に並べるのですが、スタックの追加する側と削除する側が反対です。
初めに追加したものからしかデータを取り出せないという特徴があります。
スタックとは逆で、席に入れたものを先に出す、「先入れ先出し」の仕組みを「First In First Out」、略して「FIFO」と呼びます。
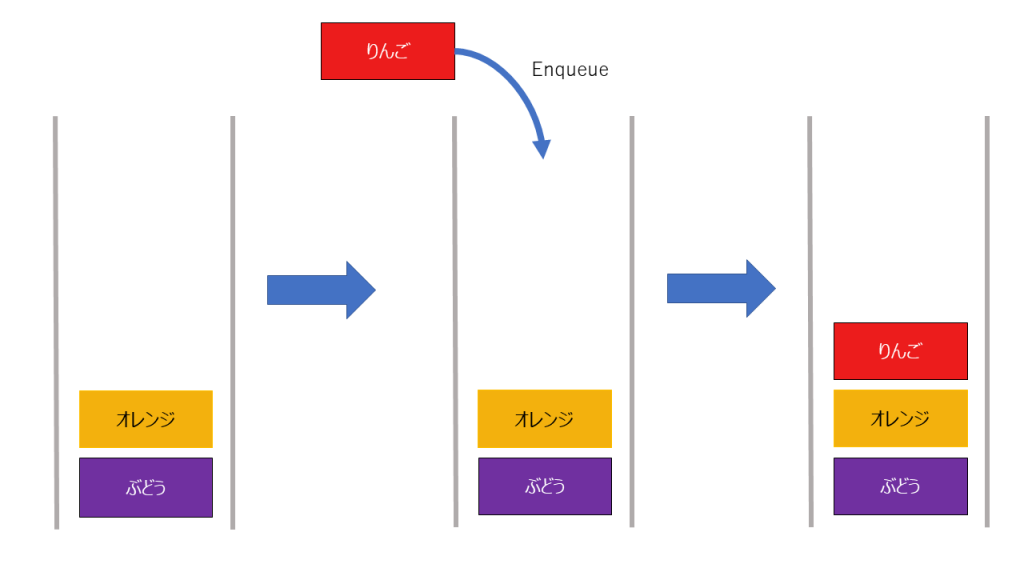
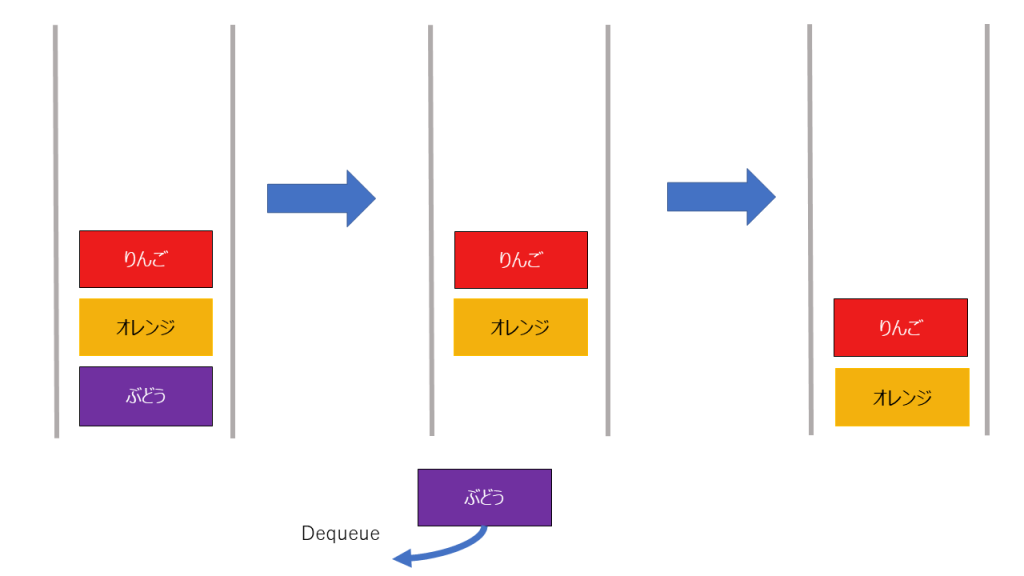
キューに詰めていく操作をenqueueと呼び、取り出す操作をdequeueと呼びます
追加、削除は以下のようになります。
追加

削除
同じく制約があるキューですが、スタックと同じような利点があります。
スタックと違うのは、データの取り出し順番だけですが、キューの利用例は早いもの勝ちのジョブをさばくようなときに使ったりします。
例えば、大繁盛のレストランのWebサイト等で、予約がいっぱいになっているときのキャンセル待ちの人のリストを管理したいといったときに利用できるかもしれません。
まとめ
- キューはデータを一列に並べ、末尾にデータを追加していくデータ構造
- データへのアクセスはリストの先頭/末尾にのみ制限されている
- データの追加、削除するスピードは速い(enqueue, dequeueともにオーダーは
 )
)
オーダーに関して
以前オーダーに関しては ![]() 等のランダウ記号で表せるという話をしました。
等のランダウ記号で表せるという話をしました。
例えば、
![]()
と表せるという話をしました。
当然間違ってはないのですが、厳密には説明が足りていません(一気に説明すると混乱すると思いましたので)。
計算量理論において、計算量の評価は以下に分類されます。
ビッグオー
今まで利用していた ![]() 等のことです。
等のことです。
大体最高次数の係数を外したものを書いておいてください的な説明だったと思いますが、本来意味は少し違います。
![]() を使う意味合いは、ざっくり言うと早くてもその関数と同じぐらいのスピードで発散するよ(これを上界といいます)という意味です。
を使う意味合いは、ざっくり言うと早くてもその関数と同じぐらいのスピードで発散するよ(これを上界といいます)という意味です。
厳密な定義を記載しますと、少し数学的な話になるんですが
ある
に関する関数
,
を考えたとき、
あるが存在して
なら
が成り立つ場合、
と表記する。
これが厳密なビッグオーの定義です。
訳分かんねぇと思うと思いますが、例を具体的に考えてみましょう。
![]() ・・・ (1)
・・・ (1)
ですと伝えたんですが、これが本当に合ってるか考えてみましょう。
そうしますと定義に合いそうな感じで一旦以下と置いてみましょう。
![]()
![]()
定義にある “ある ![]() が存在して
が存在して ![]() なら” みたいな文言が意味不明だと思いますが、
なら” みたいな文言が意味不明だと思いますが、
とても簡単に噛み砕くと、![]() を定数倍したような関数はどっかのタイミングから
を定数倍したような関数はどっかのタイミングから![]() より大きくなるよってことが言いたいだけです。
より大きくなるよってことが言いたいだけです。
例えば、
![]() vs
vs ![]() を考えてみたいと思います。
を考えてみたいと思います。
適当に大きな値を考えてみたとき、例えば ![]() くらいを考えてみたとき、
くらいを考えてみたとき、
![]()
![]()
なので![]() は
は![]() に負けてます。
に負けてます。
そして1000より大きい数字で金輪際 ![]() は
は ![]() に勝つことはありません。
に勝つことはありません。
そのため、 ![]() のとき
のとき ![]()
ということになりますね。
このとき ![]() をチョイスして定義を満たしてるので
をチョイスして定義を満たしてるので
![]() つまり(1)を満たしてるねってことが言えます。
つまり(1)を満たしてるねってことが言えます。
![]() をチョイスしましたが、もっと選べる数字はいっぱいあります。
をチョイスしましたが、もっと選べる数字はいっぱいあります。
![]() を1000と置きましたが、どっかの瞬間から超えてたら良いのでもっと緩く考えてもOKです(10000とか1億とかでも大丈夫です)。
を1000と置きましたが、どっかの瞬間から超えてたら良いのでもっと緩く考えてもOKです(10000とか1億とかでも大丈夫です)。
![]() もぶっちゃけ4より大きい数ならいずれ勝ちます。
もぶっちゃけ4より大きい数ならいずれ勝ちます。
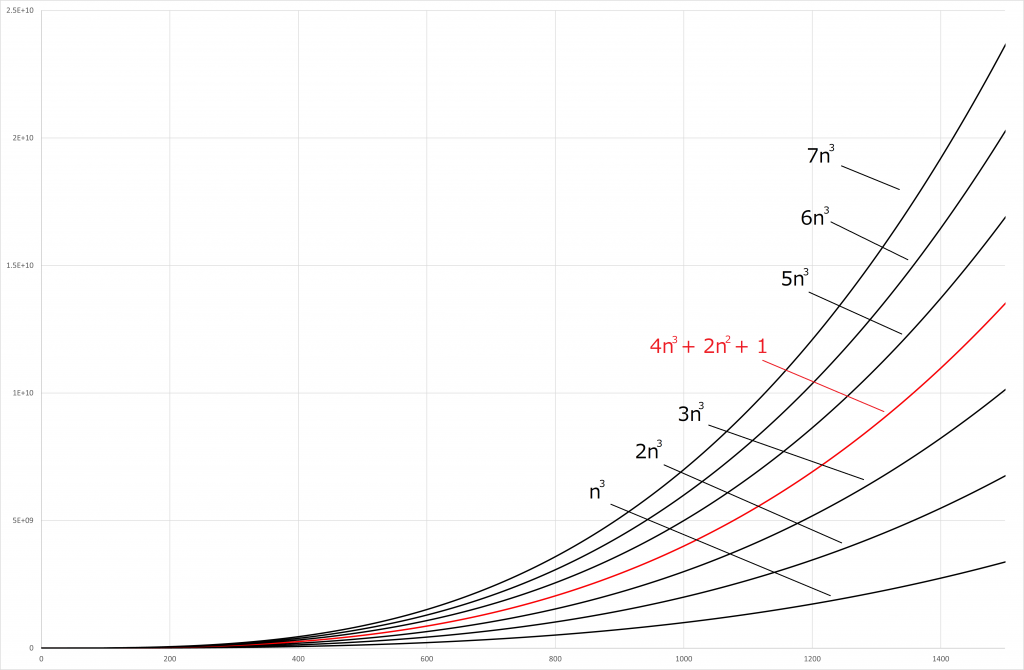
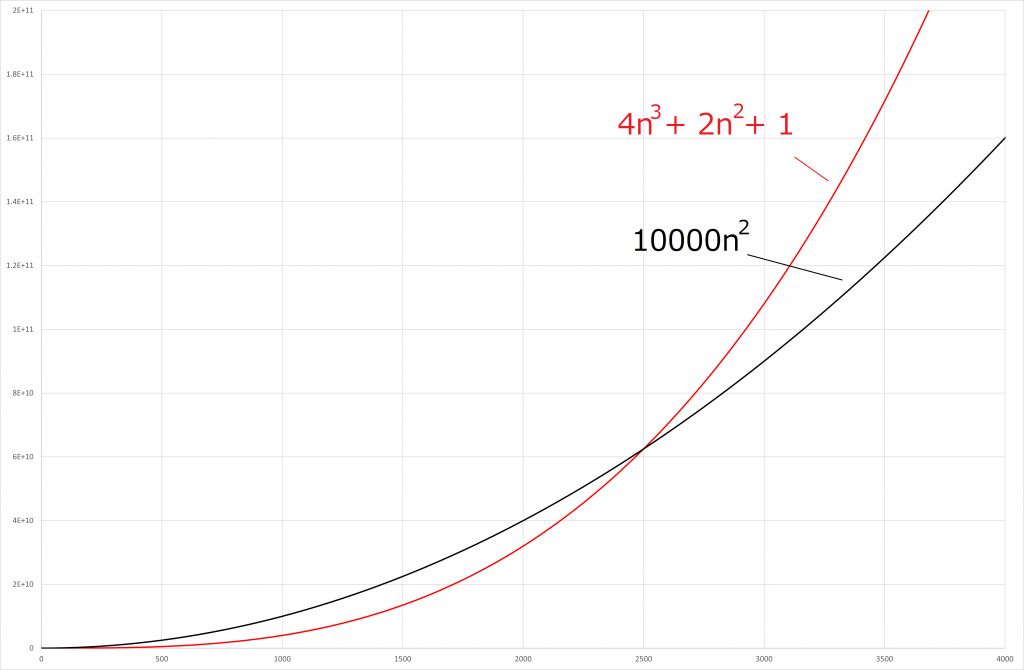
以下の図を見ていただけますと一目瞭然ですね。
赤い線で書いた関数(今回の![]() )よりも大きい関数が一つでもあれば
)よりも大きい関数が一つでもあれば![]() のオーダーとしてもOKです(ここでは
のオーダーとしてもOKです(ここでは ![]() より大きい数字では超えています)。
より大きい数字では超えています)。
ここで、じゃあ ![]() と比べたらどうなるの?とか、
と比べたらどうなるの?とか、 ![]() ならどうなるの?といったことも考えられますね。
ならどうなるの?といったことも考えられますね。
ちょっと考えてみます。
 vs
vs 

 vs
vs 

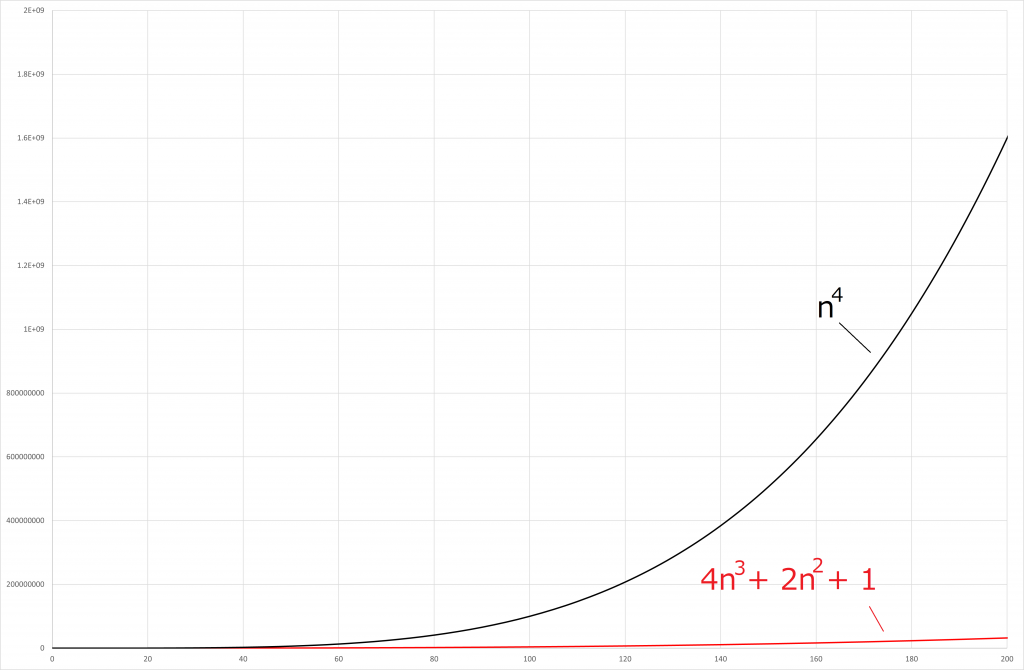
![]() は初めは勝っていますが、途中から抜かされてしまいそこから追いつくことはできません。
は初めは勝っていますが、途中から抜かされてしまいそこから追いつくことはできません。
![]() は圧勝ですね。
は圧勝ですね。
なお、![]() はある点以降数字が大きくなるので、定義に則っていますよね?
はある点以降数字が大きくなるので、定義に則っていますよね?
そのため、以下のように書くことも可能です。
![]()
しかし、 ![]() と比べると制限がゆるいので
と比べると制限がゆるいので ![]() と
と ![]() では
では ![]() のほうがより価値があると言えます。
のほうがより価値があると言えます。
ビッグオメガ
ビッグオーが上界を表しているなら、下界(遅くてもその関数と同じぐらいのスピードで発散するもの)もあるのではないかと推測することができます。
実際に存在しており、その記号を ![]() で表します。
で表します。
定義は以下です。
ある
に関する関数
,
を考えたとき、
あるが存在して
なら
が成り立つ場合、
と表記する。
上記はビッグオーと反対で ![]() を定数倍したような関数はどっかのタイミングから
を定数倍したような関数はどっかのタイミングから ![]() より小さくなるよってことが言いたいだけです。
より小さくなるよってことが言いたいだけです。
なので、説明は省略しますね。
ビッグシータ
今まで上界と下界を考えてきましたが、上界と下界が一致することがあります。
それを分かりやすい記号で ![]() と置きます。
と置きます。
度々自分は ![]() (ビッグオー)を用いてきましたが、アルゴリズムの世界において、よくビッグシータのことをビッグオーと表現することが多いので注意してください。
(ビッグオー)を用いてきましたが、アルゴリズムの世界において、よくビッグシータのことをビッグオーと表現することが多いので注意してください。
定義は以下です。
ある
に関する関数
,
を考えたとき、
あるが存在して
なら
が成り立つ場合、
と表記する。
少し表現を変えると
![]() かつ
かつ ![]() は
は ![]() の必要十分条件ということですね。
の必要十分条件ということですね。
なお、今まで例に上げてきた以下の関数は実はビッグシータで表現することができます。
![]()
まとめ
 (ビッグオー)は関数の上界を示すときに用いる記号
(ビッグオー)は関数の上界を示すときに用いる記号 (ビッグオメガ)は関数の下界を示すときに用いる記号
(ビッグオメガ)は関数の下界を示すときに用いる記号 (ビッグシータ)は関数の上界、下界が一致しているときに用いる記号
(ビッグシータ)は関数の上界、下界が一致しているときに用いる記号
上記厳密な定義ができました。
今後はできるだけこの表現を正しく用いて記事を書いていけたら良いなと思います。
アルゴリズムを考えてみる
さて、今回も前置きが長くなりましたが、本日もまたまたソートに関してアルゴリズムを考えていきます。
前回は選択ソートを考えてみましたが、今回は挿入ソートです。
挿入ソート
概要
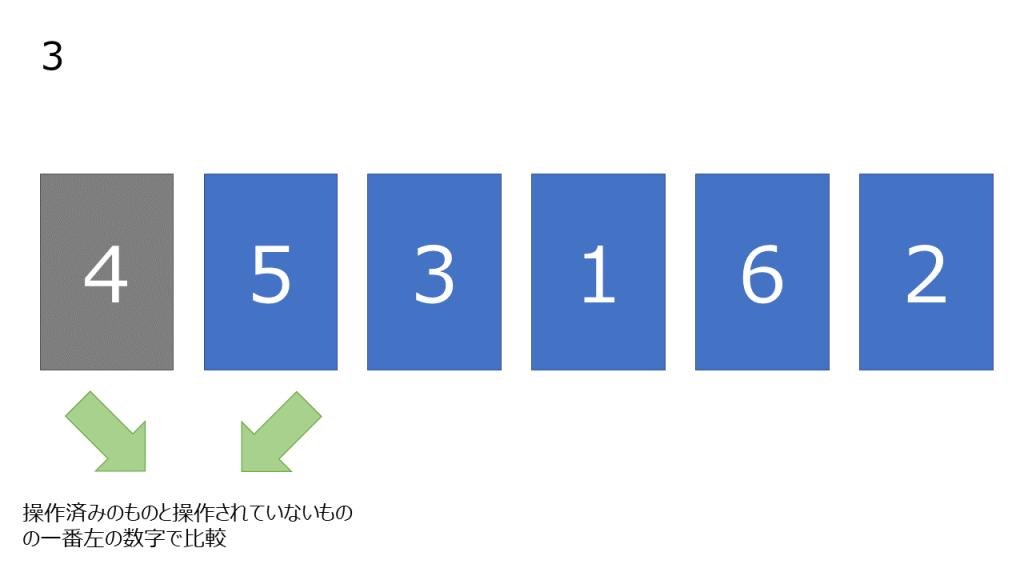
挿入ソートは数列の左側から順番にソートしていきます。左側から順に、数字を一つ取ってきてソート済みのものの適切な位置に挿入します。
処理
- 元データを用意する
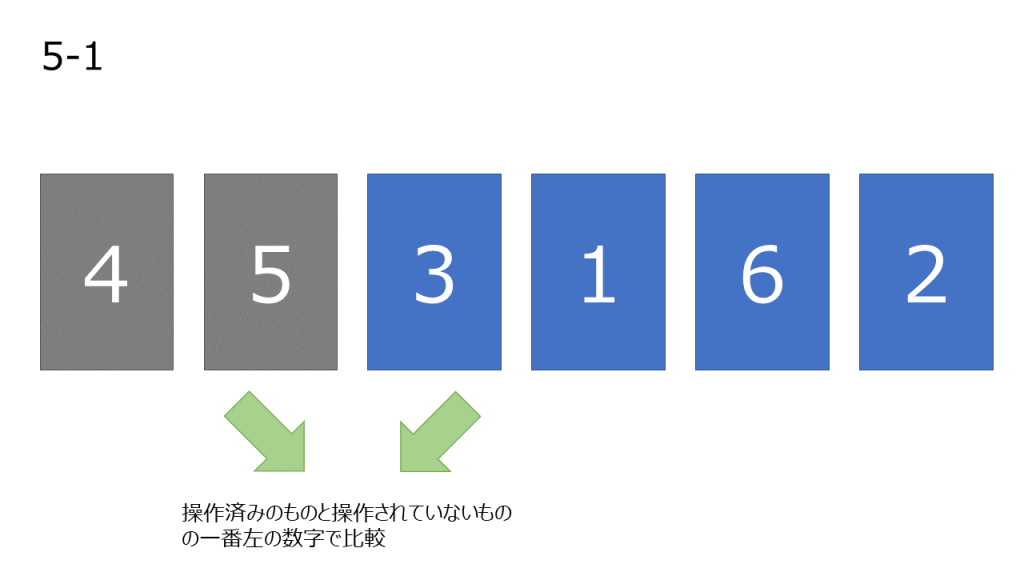
- 一番左の数字をソート済みにする
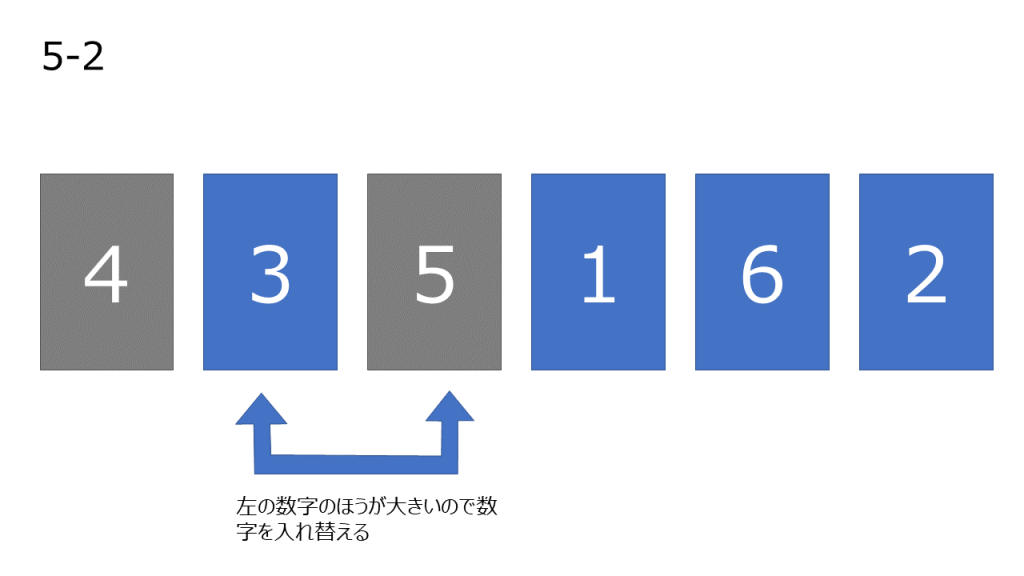
- まだ操作していない数字の中で一番左の数字を取り出し、操作済みになっている数字と比較していく。左の数字が大きい場合、2つの数字を入れ変える。この操作を自分より小さい数字が現れるか、数字が左端に到達するまで繰り返す
- 操作した数字を操作済みとする
- 3~4を繰り返し行う
- 一番右のデータ以外すべてがソート済みになったら操作を完了する
処理の上記処理








 オーダー
オーダー
オーダーは 今回はいつもと違う書き方になってしまいます。
最悪のケースの計算量は ![]()
最良のケースの計算量は ![]()
平均の計算量は ![]()
となります。
少し分かりづらいと思いますが、データの並び方によって計算量が変化すると考えていただけると分かりやすいです。
例えば、初めからソートされている数列に対しては最良の計算量が、逆順でソートされている数列に対しては最悪のケースの計算量となります。
平均ってなんぞやってところですが、すべての数字の並び方のケースの計算量を考慮してケース数で割ってあげる必要があります。
少し簡潔に書くと、
1, 2, 3という数列があった場合、数列の順番は
(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)
の6通りありますね。
これらをソートするには平均どれだけ計算したかを考えてあげましょう(計算間違えてたらすみません)。
(1, 2, 3) = 3 ステップ
(1, 3, 2) = 4 ステップ
(2, 1, 3) = 4 ステップ
(2, 3, 1) = 5 ステップ
(3, 1, 2) = 5 ステップ
(3, 2, 1) = 6 ステップ
となり、平均の計算量は ![]() となります。
となります。
今、![]() のときを考えましたが、一般的な
のときを考えましたが、一般的な ![]() に関して考えたとき、
に関して考えたとき、 ![]() に比例しているようです。
に比例しているようです。
上記のような考えで10程度({1, 2, 3, 4, 5, 6, 7, 8, 9, 10}の数列)までの整数の組み合わせを考えてみたとき以下のようになりました。
| n | 平均の計算量 |
| 2 | 2.5 |
| 3 | 4.5 |
| 4 | 7 |
| 5 | 10 |
| 6 | 13.5 |
| 7 | 17.5 |
| 8 | 22 |
| 9 | 27 |
| 10 | 32.5 |
上記の近似曲線を考えてみると、 ![]() と近似できそうでした。
と近似できそうでした。
(最悪ケースが ![]() なので、
なので、 ![]() 以上の係数の曲線は考えていません。)
以上の係数の曲線は考えていません。)
コード
例によって挿入ソートのコードを考えてみました。
コードはお馴染みのC#で書いています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
using System; using System.Collections.Generic; using System.Linq; namespace Algorithm { class Program { static void Main(string[] args) { var list = new List<int>(); // 1~20の数字をバラバラに配列に入れる for (var i = 1; i < 21; i++) { list.Add(i); } var array = list.OrderBy(x => Guid.NewGuid()).ToArray(); Console.WriteLine("{" + string.Join(",", array) + "}"); Console.WriteLine("{" + string.Join(",", InsertSort(array)) + "}"); } public static int[] InsertSort(int[] arr) { // 初めのデータはソート済みとするため、i = 1からスタート for (var i = 1; i < arr.Length; i++) { for (var sort = i; sort > 0; sort--) { // 隣の数字と大小比較。左の数字のほうが小さければ抜ける if (arr[sort] > arr[sort - 1]) { break; } var tmp = arr[sort]; arr[sort] = arr[sort - 1]; arr[sort - 1] = tmp; } } return arr; } } } |
おわりに
今回も前回までと同様の流れで進めていきました。
次回も同じ構成で進めていくと思いますが、よろしければ見ていただけますと幸いです!







 オーダー
オーダー