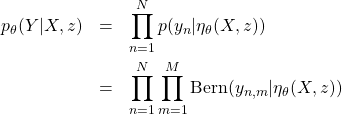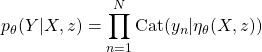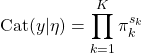はじめに
今回は生成モデルの一種であるConditional Variational Autoencoder(CVAE)を紹介する。最初に定式化を行い、その後、PythonフレームワークであるPixyzを用いた実装例を示す。最初の例として、適当な数字を指定するとその手書き文字画像を自動生成するモデルを見る。次に、手書き文字画像を与えるとその数字を予測するモデルを取り上げる。
ベイズの変分推論
![]() 個の観測値のペア
個の観測値のペア![]() を考える。
を考える。![]() とし潜在変数
とし潜在変数![]() を考え、これら3つの同時確率分布
を考え、これら3つの同時確率分布![]() にベイズの定理を適用する。
にベイズの定理を適用する。
(1) ![]()
式変形の途中で![]() を用いた(観測値
を用いた(観測値![]() と潜在変数
と潜在変数![]() は独立である)。事後確率
は独立である)。事後確率![]() をベイズの変分推論により求める。
をベイズの変分推論により求める。![]() を近似する関数としてパラメータ
を近似する関数としてパラメータ![]() を持つ関数
を持つ関数![]() を導入し、次のKullback-Leibler Divergenceを最小にすることを考える。
を導入し、次のKullback-Leibler Divergenceを最小にすることを考える。
(2) ![]()
(3) ![]()
となる。ここで、![]() は
は![]() についての期待値を表す。右辺の第3項は
についての期待値を表す。右辺の第3項は![]() に依存しないので、右辺を
に依存しないので、右辺を![]() について最小にするには次式を最小にすれば良い。
について最小にするには次式を最小にすれば良い。
(4) ![]()
ところで、![]() を用いて式(3)を変形すると
を用いて式(3)を変形すると
(5) ![]()
を得る。Kullback-Leibler Divergenceは常に0以上であるから
(6) ![]()
となる。左辺の量![]() はEvidenceと呼ばれる量であり、この対数の下限が
はEvidenceと呼ばれる量であり、この対数の下限が![]() であることを上式は示している。この下限をEvidence Lower Bound(ELBO)と呼ぶ。すなわち、ELBOを最大することと、
であることを上式は示している。この下限をEvidence Lower Bound(ELBO)と呼ぶ。すなわち、ELBOを最大することと、![]() を最小にすることとは等価である。いずれにせよ、式(4)を最小するような
を最小にすることとは等価である。いずれにせよ、式(4)を最小するような![]() を見つけることが目標になる。
を見つけることが目標になる。
深層生成モデル
確率分布![]() を正規分布で表し、そのパラメータである平均
を正規分布で表し、そのパラメータである平均![]() と分散
と分散![]() をネットワークを用いて計算する。
をネットワークを用いて計算する。
(7) ![]()
ここで、![]() は
は![]() の関数であり、パラメータ
の関数であり、パラメータ![]() はネットワークの各種重みに相当する。ネットワークを用いて表現された生成モデルを深層生成モデルと呼ぶ。ここでは手書き文字画像のデータセットMNISTを用いて、次の二通りの生成モデルを考える。
はネットワークの各種重みに相当する。ネットワークを用いて表現された生成モデルを深層生成モデルと呼ぶ。ここでは手書き文字画像のデータセットMNISTを用いて、次の二通りの生成モデルを考える。
 を数字、
を数字、 を画像とみなす。このとき、
を画像とみなす。このとき、 は数字
は数字 と潜在変数
と潜在変数 から画像
から画像 を生成するモデルになる。この生成モデルを「生成モデル1」と呼ぶことにする。
を生成するモデルになる。この生成モデルを「生成モデル1」と呼ぶことにする。 としてベルヌーイ分布を仮定する。
としてベルヌーイ分布を仮定する。
(8)

 は個々の画素を指定する番号である。ベルヌーイ分布
は個々の画素を指定する番号である。ベルヌーイ分布 は次式で定義される。
は次式で定義される。(9)

ここで、
 は
は を満たす実数である。ベルヌーイ分布は0か1のいずれかを生成する。すなわち、MNIST画像を2値画像とみなすということである(実際はグレイ画像だけど)。パラメータ
を満たす実数である。ベルヌーイ分布は0か1のいずれかを生成する。すなわち、MNIST画像を2値画像とみなすということである(実際はグレイ画像だけど)。パラメータ を、入力を
を、入力を とするネットワークで計算する。
とするネットワークで計算する。 はネットワークの重みを表す。
はネットワークの重みを表す。 を画像、
を画像、 を数字とみなす。このとき、
を数字とみなす。このとき、 は画像
は画像 と潜在変数
と潜在変数 から数字
から数字 を生成するモデルになる。この生成モデルを「生成モデル2」と呼ぶことにする。
を生成するモデルになる。この生成モデルを「生成モデル2」と呼ぶことにする。 としてカテゴリカル分布を仮定する。
としてカテゴリカル分布を仮定する。
(10)

パラメータ
 を、入力を
を、入力を とするネットワークで計算する。
とするネットワークで計算する。 はネットワークの重みを表す。カテゴリカル分布は次式で定義される確率分布である。
はネットワークの重みを表す。カテゴリカル分布は次式で定義される確率分布である。(11)

ただし、
 は0か1のどちらかの値をとり、かつ
は0か1のどちらかの値をとり、かつ である。また、
である。また、 は、
は、 、かつ
、かつ を満たす実数である。
を満たす実数である。 は1から
は1から までのいずれかの整数値を取る。
までのいずれかの整数値を取る。
生成モデル1、生成モデル2のどちらのモデルにおいても![]() として標準正規分布を仮定する。
として標準正規分布を仮定する。
(12) ![]()
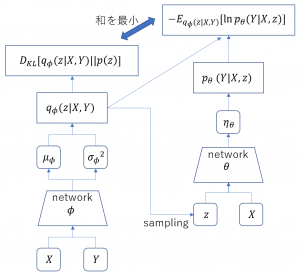
ここまでの様子を図にすると以下のようになる。
結果
深層生成モデルのためのPythonフレームワークPixyzを用いて実装した。ソースはここにある。最初に、標準正規分布![]() から発生させた乱数
から発生させた乱数![]() と数字5(
と数字5(![]() )のペアから生成した手書き文字画像(
)のペアから生成した手書き文字画像(![]() )を示す(生成モデル1)。
)を示す(生成モデル1)。

左図は1epochの訓練後、右図は10epochの訓練後の生成画像である。64個の乱数を発生させ、それぞれに対応する画像を示した。次に再構成画像を示す。![]() のあと
のあと![]() により再構成された画像
により再構成された画像![]() に相当する。
に相当する。

左図下の段は1epochの訓練後の再構成画像、右図下の段は10epochの訓練後の再構成画像である。上の段は左右ともに元画像である。
次に、画像と乱数を与えて、数字をあてる生成モデル(予測器)の精度を示す。これは生成モデル2の結果である。
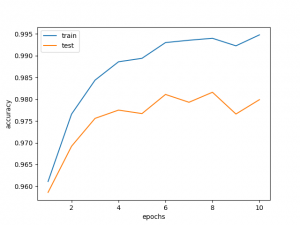
各エポックの終わりに![]() から乱数
から乱数![]() を発生させ(訓練データについては5万個、テストデータについては1万個)、訓練データ・テストデータが持つ画像
を発生させ(訓練データについては5万個、テストデータについては1万個)、訓練データ・テストデータが持つ画像![]() を用いて、カテゴリカル分布
を用いて、カテゴリカル分布![]() によりラベルを予測し、精度を測定した。特に優れた結果になるわけではないが、生成モデルを予測器として使えるのは純粋に面白いと思う。
によりラベルを予測し、精度を測定した。特に優れた結果になるわけではないが、生成モデルを予測器として使えるのは純粋に面白いと思う。
Pixyzの特長
今回の生成モデル1のソースコードを取り上げ、Pixyzの特長を解説する。まず最初に、![]() を実装した部分である。
を実装した部分である。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# q(z|x,y) class Inference(Normal): def __init__(self): super().__init__(var=["z"], cond_var=["x", "y"], name="q") self.fc1 = nn.Linear(X_DIM + Y_DIM, H_DIM) self.fc2 = nn.Linear(H_DIM, H_DIM) self.fc31 = nn.Linear(H_DIM, Z_DIM) self.fc32 = nn.Linear(H_DIM, Z_DIM) def forward(self, x, y): h = F.relu(self.fc1(torch.cat([x, y], 1))) h = F.relu(self.fc2(h)) # scale is variance return {"loc": self.fc31(h), "scale": F.softplus(self.fc32(h))} |
先に説明したように
(13) ![]()
と仮定した。これを表現するため、正規分布クラスNormalを継承している(2行目)。さらに、平均locと分散scaleをネットワークで計算させている(13から16行目)。Normalを継承したクラスは、メソッドforwardでlocとscaleを返さなければならない仕様になっている。この約束により、クラスInferenceは正規分布として働くことができる。
次に![]() を実装した部分である。コード内で
を実装した部分である。コード内で![]() と
と![]() の表記が逆になっているのは実装上の都合のためである。読み替えて見てほしい。
の表記が逆になっているのは実装上の都合のためである。読み替えて見てほしい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# p(x|z,y) class Generator(Bernoulli): def __init__(self): super().__init__(var=["x"], cond_var=["z", "y"], name="p") self.fc1 = nn.Linear(Z_DIM + Y_DIM, H_DIM) self.fc2 = nn.Linear(H_DIM, H_DIM) self.fc3 = nn.Linear(H_DIM, X_DIM) def forward(self, z, y): h = F.relu(self.fc1(torch.cat([z, y], 1))) h = F.relu(self.fc2(h)) return {"probs": torch.sigmoid(self.fc3(h))} |
先に見たようにベルヌーイ分布を用いて
(14) 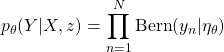
と仮定した。これを表現するため今度はBeroulliクラスを継承している(2行目)。そしてパラメータ![]() を計算するためネットワークを用いている(12から14行目)。
を計算するためネットワークを用いている(12から14行目)。probsは![]() に相当する。メソッド
に相当する。メソッドforwardでprobsを返すことにより、クラスGeneratorはベルヌーイ分布として働くことができる。
二つの例で見たように、あらかじめ用意されている確率分布NormalBernoulliを継承することで容易に目的とする確率分布を実装することができる。これら2つの確率分布、![]() から計算される最小にすべき量
から計算される最小にすべき量
(15) ![]()
は以下のようにコーディングされる。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# p(x|y,z) p = net.Generator().to(device) # q(z|x,y) q = net.Inference().to(device) # prior p(z) prior = Normal(loc=torch.tensor(0.0), scale=torch.tensor(1.0), var=["z"], features_shape=[net.Z_DIM], name="p_{prior}").to(device) loss = (KullbackLeibler(q, prior) - Expectation(q, LogProb(p))).mean() model = Model(loss=loss, distributions=[p, q], optimizer=optim.Adam, optimizer_params={"lr": 1e-3}) |
2行目で![]() を、5行目で
を、5行目で![]() を、8行目で
を、8行目で![]() (標準正規分布)を作っている。そして、11行目で式(15)を計算している。
(標準正規分布)を作っている。そして、11行目で式(15)を計算している。KullbackLeiblerExpectationLogProbはいずれもPixyzが用意しているモジュールである。12行目では、勾配降下法を行うためのモデルを作っている。このように、ほぼ理論式のままコーディングできるエレガントさがPixyzの大きな特長である。
まとめ
今回は生成モデルの1つであるConditional Variational Autoencoder(CVAE)を取り上げ、確率分布のパラメータを計算する過程にネットワークを導入した。このようにネットワークを利用した生成モデルを深層生成モデルと呼ぶ。さらに、MINISTを用いた応用例をPixyzを用いて実装し、その結果を示した。Pixyzを用いると、ほぼ理論式のままコーディングすることができる。深層学習の中でも深層生成モデルは今後も発展する分野であると考えている。