はじめに
以前の投稿でラグランジュの未定乗数法を扱った。今回はそれを一般化し、KKT条件と呼ばれる一連の条件式を導く。
問題設定
(1) ![]()
で与えられるとき、![]() の極値を求めるには、関数
の極値を求めるには、関数
(2) ![]()
を考え、![]() の
の![]() と
と![]() についての極値を計算すればよい。ここで、関数
についての極値を計算すればよい。ここで、関数![]() をラグランジュ関数と呼ぶのであった。今回は、束縛条件を不等号に拡張する。
をラグランジュ関数と呼ぶのであった。今回は、束縛条件を不等号に拡張する。
(3) ![]()
さらに、![]() の極値ではなく最小値(条件を満たす領域における最小値)を考える。まとめると、今回の問題設定は以下のようになる。
の極値ではなく最小値(条件を満たす領域における最小値)を考える。まとめると、今回の問題設定は以下のようになる。
(4)
(5)
の最小値を求めよ。
ラグランジュの未定乗数法
見通しをよくするため、先の記事の例題で用いた関数 ![]() を考える。下図の緑色の放物曲面が
を考える。下図の緑色の放物曲面が![]() である。ここに、
である。ここに、![]() の領域
の領域![]() (赤色の円柱内部)を重ねてみる。
(赤色の円柱内部)を重ねてみる。
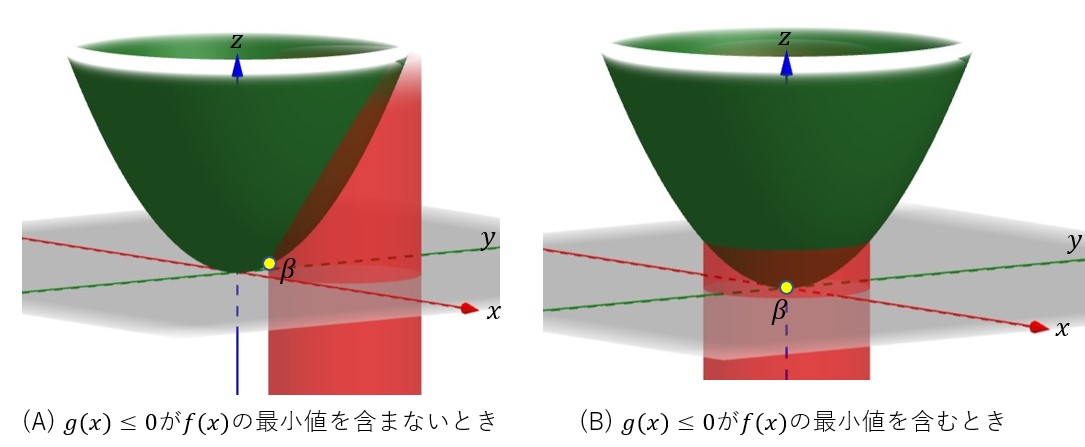
(A)は![]() のとき、(B)は
のとき、(B)は![]() のときである。(A)の場合、
のときである。(A)の場合、![]() の縁で最小(
の縁で最小(![]() )となり、(B)の場合、
)となり、(B)の場合、![]() の最小値がそのまま解(
の最小値がそのまま解(![]() )となる。この観察を定式化する。
)となる。この観察を定式化する。
まず最初に(A)を考える。最小値![]() は領域
は領域![]() の縁上にあるから
の縁上にあるから![]() が成り立つ。いま、点
が成り立つ。いま、点![]() を微小量
を微小量![]() だけ
だけ![]() からはみ出さない方向に動かす。このとき次式が成り立つ。
からはみ出さない方向に動かす。このとき次式が成り立つ。
(6) ![]()
(7) ![]()
が成り立つ。点![]() における
における![]() の等高線と
の等高線と![]() は点
は点![]() で接するから、
で接するから、![]() と
と![]() は同じ向きを持つか、真逆の向きを持つ。同じ向きを持つ場合、
は同じ向きを持つか、真逆の向きを持つ。同じ向きを持つ場合、![]() として
として
(8) ![]()
(9) ![]()
となる。ここで![]() における
における![]() の値を評価すると
の値を評価すると
(10) ![]()
いま、![]() であったから
であったから![]() となる。これは
となる。これは![]() が最小値であることと矛盾する。したがって、
が最小値であることと矛盾する。したがって、![]() と
と![]() は反平行でなければならない。
は反平行でなければならない。
(11) ![]()
ここでラグランジュ関数![]()
(12) ![]()
を導入すれば、(A)の場合の最小値は次式を解けばよいことが分かる。
(13) 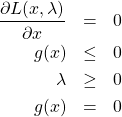
式(13)の4つ目の式![]() は最小値が
は最小値が![]() の縁にあることを表している。
の縁にあることを表している。
次に(B)の場合を考える。このときは領域![]() が
が![]() の最小値を含むから束縛条件なしで
の最小値を含むから束縛条件なしで![]() の最小値を求めればよい。これはラグランジュ関数において
の最小値を求めればよい。これはラグランジュ関数において![]() と置くことを意味する。
と置くことを意味する。
(A)と(B)の2つの結果を融合すると解くべき式は以下となる。
(14) 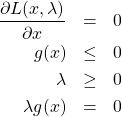
式(14)の4つ目の条件![]() は、(A)の場合は
は、(A)の場合は![]() を、(B)の場合は
を、(B)の場合は![]() を意味する。式(14)の4つの式のセットを、カルーシュ・キューン・タッカー条件(Karush-Kuhn-Tucker condition)あるいはKKT条件と呼ぶ。
を意味する。式(14)の4つの式のセットを、カルーシュ・キューン・タッカー条件(Karush-Kuhn-Tucker condition)あるいはKKT条件と呼ぶ。
まとめ
今回は、以前紹介したラグランジュの未定乗数法を一般化し、KKT条件と呼ばれる式のセットを導出した。これは最適化問題における主問題と双対問題の間を橋渡しするものであり、SVMなどの最適化問題を解く際には必ず現れる重要な条件である。主問題と双対問題の説明は機会を改めたい。

