はじめに
最近見た教育系Youtuberが扱っていた「正多面体が5種類しかないことの証明」が面白かったので紹介したい。
正多面体
正多面体は5種類しかないことが知られている（下図参照：ここから引用した）。
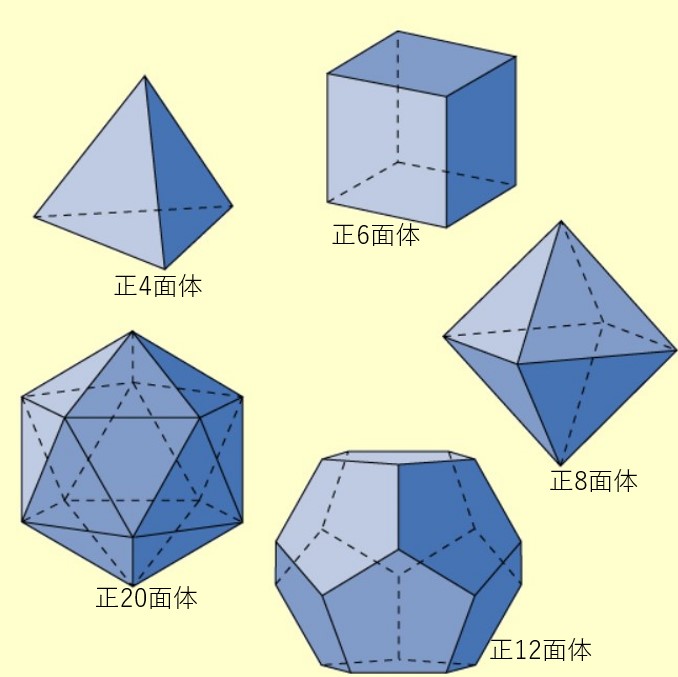
各正多面体の属性一覧は以下の通り。
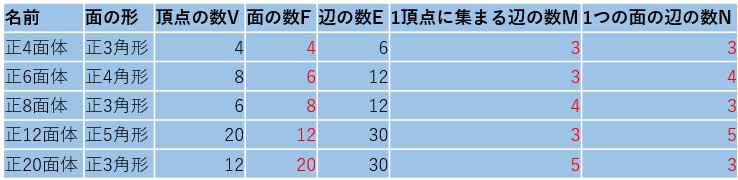
余談であるが、弊社の3D類似検索では正12面体の20個の頂点を利用している。
オイラーの多面体定理
正多面体が5種類しかないことを証明する方法はいくつかあるが、ここではオイラーの多面体定理を出発点とする。この定理の証明は今回は行わない。
穴の開いていない多面体については、頂点の数
、面の数
、面の数
について次式が成り立つ。
例えば正4面体の場合、
、
、
なので
となり、上式が成り立つことが分かる。他の正多面体ついても同様である。
正多面体が5種類しかないことの証明
1つの頂点に集まる辺の数を
、1つの面の辺の数を
とする。このとき次が成り立つ。
(1) 
例えば正四面体の場合、
、
である。正四面体の面の数は、辺の数はであるから、
が成り立つ。さらに、頂点の数はであるから
も成り立つ。
式(1)の1番目の式より
式(1)の2番目の式より
上の2つの式をオイラーの多面体定理に代入する。
(2) 
を得る。この式が、正多面体であるとき成り立たなければならない条件（必要条件）である。これを満たす整数の組
が正多面体の候補となる。
整数問題
正多面が満たすべき条件（必要条件）は式(2)に帰着した。ここではこの式を満たす3つの整数の組を求める。ただし、
は面の数、は1つの頂点に集まる辺の数、は1つの面の辺の数であるからいずれの数も3以上である。
式(2)の両辺に
をかける。
(3) 
これを変形すると
右辺は正の数なので
でなければならない。従って
が成り立つ。この式を満たす整数
の組は容易に見つけることができる。
各に対し、式(3)からを求めると
となる。最初に示した正多面体の属性一覧をもう一度示す。
整数問題として解いた5つの解は、上の赤字（実際に存在している正多面体）と一致していることが分かる（十分条件）。以上より正多面体は5種類しか存在しないことが示された。
まとめ
リンクを貼った動画では、最初に式(2)が大学入試問題として紹介されており、解法を示したあと同じ式が正多面体が5種類しかないことの証明に使われることに言及している。たかが入試問題されど入試問題である。
