はじめに
今回は、「次元の呪い」に関連した3つの話題を解説する。
次元の呪いとは?
次元の呪い(The curse of dimensionality)とは、次元数を高くしたとき、3次元までの常識からは予想できない特異な振る舞いが出現することである。リチャード・ベルマン(強化学習で有名なベルマン方程式のひと)が1957年の論文で初めて使った概念である。以下3つの具体例で見られる高次元の特異な振る舞いを解説する。
- 高次元空間における球の体積と表面積の比
- 高次元空間における球の体積と球に外接する立方体の体積の比
- 高次元正規分布
高次元空間における球の体積と表面積の比
最初に、2次元空間内の半径![]() の円を考える。このとき、円周
の円を考える。このとき、円周![]() と面積
と面積![]() は次式で与えられる。
は次式で与えられる。
(1) ![]()
次に、3次元空間内の半径![]() の球の表面積
の球の表面積![]() と体積
と体積![]() を考える。
を考える。
(2) 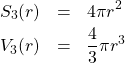
一般に、![]() 次元空間における球(これを超球と呼ぶ)の表面積
次元空間における球(これを超球と呼ぶ)の表面積![]() と体積
と体積![]() は次式で与えられる。
は次式で与えられる。
(3) 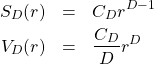
ここで、![]() は定数であり、
は定数であり、![]() 、
、![]() である。
である。![]() の正確な表式は、例えばBishop本の演習問題に掲載されている。表面積と体積の比を取ると次式を得る。
の正確な表式は、例えばBishop本の演習問題に掲載されている。表面積と体積の比を取ると次式を得る。
(4) ![]()
したがって、![]() のとき、式(4)の右辺は0になる。すなわち、次元が高くなるほど体積よりも表面積からの寄与が大きくなるのである。このことはよく、次のように例えられることが多い。
のとき、式(4)の右辺は0になる。すなわち、次元が高くなるほど体積よりも表面積からの寄与が大きくなるのである。このことはよく、次のように例えられることが多い。
高次元空間における球の体積と球に外接する立方体の体積の比
最初に2次元空間を考える。半径![]() の円の面積
の円の面積![]() と円に外接する正方形の面積
と円に外接する正方形の面積![]() は次式で与えられる。
は次式で与えられる。
(5) ![]()
次に、3次元空間を考える。半径![]() の球の体積
の球の体積![]() と球に外接する立方体の体積
と球に外接する立方体の体積![]() は次式で与えられる。
は次式で与えられる。
(6) 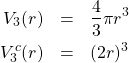
一般に、![]() 次元空間における立方体(これを超立方体と呼ぶ)の体積
次元空間における立方体(これを超立方体と呼ぶ)の体積![]() は次式で与えられる。
は次式で与えられる。
(7) ![]()
(8) ![]()
![]() のとき、式(8)の右辺は0になることを示すことができる(証明はBishop本の演習問題にある)。すなわち、高次元空間においては、球の体積の寄与が減るのである。
のとき、式(8)の右辺は0になることを示すことができる(証明はBishop本の演習問題にある)。すなわち、高次元空間においては、球の体積の寄与が減るのである。
さて、球の中心(立方体の中心でもある)から立方体の1つの角までの距離は![]() であるから(下図参照)、
であるから(下図参照)、
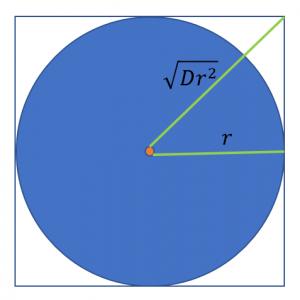
球の半径![]() との比をとると
との比をとると
(9) ![]()
となる。![]() のとき、式(9)の右辺は
のとき、式(9)の右辺は![]() になる。すなわち、高次元空間における立方体の角は刺のように鋭く(スパイク状に)伸びていることになる。また、立方体の角の数は
になる。すなわち、高次元空間における立方体の角は刺のように鋭く(スパイク状に)伸びていることになる。また、立方体の角の数は![]() であるから、
であるから、![]() のとき、角の数も
のとき、角の数も![]() になる。
になる。
ここで、モンテカルロ法を用いた![]() の算出手順を紹介したい。図のような半径1の扇形を考え、以下の手順を行うことで
の算出手順を紹介したい。図のような半径1の扇形を考え、以下の手順を行うことで![]() の近似値を得ることができる。
の近似値を得ることができる。
- 変数
 を0で初期化する。
を0で初期化する。 - [0,1]の間の実数値を生成する乱数器を用いて座標
 を作る。
を作る。 - この座標が扇形内
 にあれば
にあれば に1を加算する。
に1を加算する。 - この手順を適当な回数
 だけ繰り返す。
だけ繰り返す。 - 最後に
 を4倍すれば
を4倍すれば の近似値を得る。
の近似値を得る。
ここで行っていることは、正方形内に生成した座標のうち、扇形内にある点だけを選ぶことである。これを高次元空間で考えた場合どうなるか。既に見たように高次元では、立方体(超立方体)に占める球(超球)の体積の割合は小さくなる。つまり、高次元になるほど、乱数で生成した座標が球内に収まる確率が小さくなっていくことになる。言い換えると、精度良く![]() を求めるのに必要な座標の数が多くなっていくことになる。この現象は、次元の呪いが数値計算に及ぼす悪影響として良く取り上げられる。
を求めるのに必要な座標の数が多くなっていくことになる。この現象は、次元の呪いが数値計算に及ぼす悪影響として良く取り上げられる。
高次元正規分布
ここでは、高次元正規分布の振る舞いを見る。いま、![]() 次元の等方的な正規分布を考える。
次元の等方的な正規分布を考える。
(10) ![]()
ただし![]() である。このとき、確率分布
である。このとき、確率分布![]() の下での、ある量
の下での、ある量![]() の期待値
の期待値![]() は次式で与えられる。
は次式で与えられる。
(11) ![]()
積分範囲は全空間である。ここで、極座標変換を行う。![]() が中心からの距離
が中心からの距離![]() だけに依存する場合、上式は以下のように変形することできる。
だけに依存する場合、上式は以下のように変形することできる。
(12) ![Rendered by QuickLaTeX.com \begin{eqnarray*} E[f]&=&\int_0^{\infty} dr f(r)q_D(r) \\ q_D(r)&=&\frac{C_D\;r^{D-1}}{(2\pi\sigma^2)^{D/2}}\exp{\left(-\frac{r^2}{2\sigma^2}\right)} \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-6b8903203d38f0be1721af407c4a0618_l3.png)
![]() は既出の定数である。ここで、関数
は既出の定数である。ここで、関数![]() に指数函数だけでなく、
に指数函数だけでなく、![]() 次の項(
次の項(![]() )が現れることが重要である(この事実は、極座標変換を行ったとき
)が現れることが重要である(この事実は、極座標変換を行ったとき![]() が角度依存性も持つ場合でも成り立つ)。関数
が角度依存性も持つ場合でも成り立つ)。関数![]() の様子を下に示す。
の様子を下に示す。
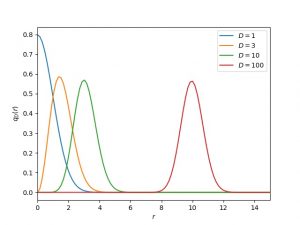
![]() が大きくなるに従い、極大値の位置が中心から離れていくことが分かる。極大値の位置
が大きくなるに従い、極大値の位置が中心から離れていくことが分かる。極大値の位置![]() は
は![]() を微分すれば容易に求めることができ、
を微分すれば容易に求めることができ、![]() となる。以上の事実を踏まえて期待値の式
となる。以上の事実を踏まえて期待値の式
(13) ![]()
を眺めると、次元が高くなるほど![]() の中心近傍の振る舞いが結果に反映されなくなることが分かる。この現象は、既に見た球の体積と表面積の関係や、球と立方体の体積の関係とよく似ている。高次元ほど、中心ではなく端の影響が大きくなるのである。
の中心近傍の振る舞いが結果に反映されなくなることが分かる。この現象は、既に見た球の体積と表面積の関係や、球と立方体の体積の関係とよく似ている。高次元ほど、中心ではなく端の影響が大きくなるのである。
このことは、高次元正規分布を用いてサンプルされる点のほとんどは、球の表面近傍の点であると表現することもできる。これはモンテカルロ法などサンプリングを必要とする数値計算を行うときに注意しなければならない点である。
まとめ
今回は、高次元空間では直観とは異なる現象が起きていることを見た。球の表面積と体積の関係や、立方体と球の体積の関係で解説したように、高次元空間内の点は、そのほとんどが中心から離れた薄い皮の表面にへばりつくように分布する。この事実が計算効率を落としたり、精度を維持するために膨大な数のデータ(空間内の点に対応する)を必要とする原因となる。同じ現象が正規分布でも起きていることを示した。機械学習や深層学習では高次元ベクトルを当たり前のように扱うが、「次元の呪い」があることに留意しなければならない。

