はじめに
先の回では「量子もつれ」という現象を紹介し、blueqatという名前のフレームワークを用いて量子もつれをシミュレートした。今回は、離散フーリエ変換を量子コンピュータ(量子回路)で行うアルゴリズム「量子フーリエ変換」を紹介し、先と同じようにblueqatでシミュレートする。
離散フーリエ変換
(1) 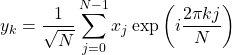
(2) ![]()
を定義すると、式(1)は
(3) 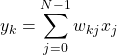
と書くことができる。![]() を成分に持つ行列
を成分に持つ行列![]() を導入すると、式(3)は
を導入すると、式(3)は
(4) ![]()
と書ける。ここで、![]() である。行列
である。行列![]() はユニタリー行列になっていることに注意する。すなわち
はユニタリー行列になっていることに注意する。すなわち
(5) ![]()
が成り立つ。ここで、![]() は
は![]() のエルミート共役(転置して複素共役をとる)を表す。
のエルミート共役(転置して複素共役をとる)を表す。![]() は単位行列である。ユニタリー性を満たさない演算は量子回路上に載せることができないので、離散フーリエ変換のユニタリー性(式(5))は重要である。
は単位行列である。ユニタリー性を満たさない演算は量子回路上に載せることができないので、離散フーリエ変換のユニタリー性(式(5))は重要である。
振幅エンコーディング
![]() や
や![]() のようなベクトルをどのように量子コンピュータに載せるのかを考える。これまでのブログ(1,2)で1量子ビットと2量子ビットを扱った。任意の量子状態は、1量子ビットの場合は
のようなベクトルをどのように量子コンピュータに載せるのかを考える。これまでのブログ(1,2)で1量子ビットと2量子ビットを扱った。任意の量子状態は、1量子ビットの場合は![]() の2つの基底状態の重ね合わせで、2量子ビットの場合は
の2つの基底状態の重ね合わせで、2量子ビットの場合は![]() の4つの基底状態の重ね合わせで表現されることを見た。ここで、0や1の並びは0以上の整数の2進数表記に相当し、2量子ビットの場合の00,01,10,11は、それぞれ、10進数表記で0,1,2,3に相当する。いま、4次元の単位ベクトル
の4つの基底状態の重ね合わせで表現されることを見た。ここで、0や1の並びは0以上の整数の2進数表記に相当し、2量子ビットの場合の00,01,10,11は、それぞれ、10進数表記で0,1,2,3に相当する。いま、4次元の単位ベクトル![]() が与えられたとき、各成分を係数に持つ次の量子状態を考える。
が与えられたとき、各成分を係数に持つ次の量子状態を考える。
(6) 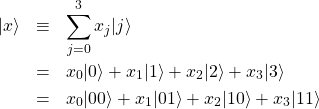
![]() は単位ベクトルとしたから量子状態が満たすべき条件(規格化条件:
は単位ベクトルとしたから量子状態が満たすべき条件(規格化条件:![]() )は満たされている。つまり、4次元ベクトルは2量子ビットを用いて上のように表すことができる。これを
)は満たされている。つまり、4次元ベクトルは2量子ビットを用いて上のように表すことができる。これを![]() ビットに拡張する。
ビットに拡張する。
(7) 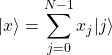
ただし、![]() である。式(7)は
である。式(7)は![]() 次元ベクトルを表す量子状態である。
次元ベクトルを表す量子状態である。![]() なら
なら
(8) 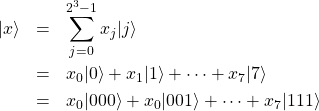
となり、8(![]() )次元ベクトルを表すことができる。このようにベクトルの成分を量子状態の係数(確率振幅)に埋め込むことを振幅エンコーディングと呼ぶ。どのようにしてこの状態を作り出すのかという話は少々複雑なので今回は言及しない。
)次元ベクトルを表すことができる。このようにベクトルの成分を量子状態の係数(確率振幅)に埋め込むことを振幅エンコーディングと呼ぶ。どのようにしてこの状態を作り出すのかという話は少々複雑なので今回は言及しない。
量子フーリエ変換
(9) 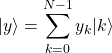
ここに式(3)を代入すると
(10) ![Rendered by QuickLaTeX.com \begin{eqnarray*} |y\rangle &=& \sum_{k=0}^{N-1}y_k|k\rangle \\ &=& \sum_{k=0}^{N-1}\left[\sum_{j=0}^{N-1}w_{kj}x_j\right]|k\rangle \\ &=& \sum_{j=0}^{N-1} x_j \left[\sum_{k=0}^{N-1}w_{kj}|k\rangle\right] \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-5d2cdc1c6be53b1c1fe59452c874a8de_l3.png)
(11) 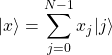
であった。この2式を見比べると、![]() から
から![]() に変換するには次の変換を行えばよいことが分かる。
に変換するには次の変換を行えばよいことが分かる。
(12) 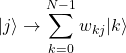
(13) 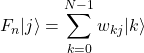
(14) ![Rendered by QuickLaTeX.com \begin{eqnarray*} F_n|x\rangle &=& F_n\sum_{j=0}^{N-1}x_j|j\rangle \\ &=& \sum_{j=0}^{N-1}x_j\left(F_n|j\rangle\right) \\ &=& \sum_{j=0}^{N-1}x_j\left[\sum_{k=0}^{N-1}w_{kj}|k\rangle\right] \\ &=& \sum_{k=0}^{N-1}\left[\sum_{j=0}^{N-1}w_{kj}x_j\right]|k\rangle \\ &=& \sum_{k=0}^{N-1}y_k|k\rangle \\ &=& |y\rangle \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-4e8a94a52d20ab8dfb43ad2dd5458469_l3.png)
となる。変換![]() を量子フーリエ変換(Quantum Fourier Transform:QFT)と呼ぶ。上式を見ると、
を量子フーリエ変換(Quantum Fourier Transform:QFT)と呼ぶ。上式を見ると、![]() の結果からフーリエ係数
の結果からフーリエ係数![]() を求めるには
を求めるには![]() の係数を取り出す必要があることに注意しなければならない。これを行う手間についてはまた後で触れることにする。
の係数を取り出す必要があることに注意しなければならない。これを行う手間についてはまた後で触れることにする。
QFTアルゴリズム(ステップ1)
QFTを量子回路に載せる手順(QFTアルゴリズム)を説明する。まず最初に、QFTの式を量子回路に載せやすい形に変形する必要がある。ステップ1ではその変形の過程を示す。古典回路と同様に量子回路の場合も2進数の言葉で書き直す必要がある。
(15) 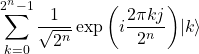
となる。ところで、![]() の
の![]() ビット2進数表記が
ビット2進数表記が![]() となるとき(例えば、3の2進数表記は11なので
となるとき(例えば、3の2進数表記は11なので![]() )、次式が成り立つ。
)、次式が成り立つ。
(16) 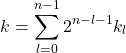
(17) ![]()
となる。表記を簡単にするため直積記号![]() は省略した。さらに
は省略した。さらに![]() についての和は次のように書き直すことができる。
についての和は次のように書き直すことができる。
(18) 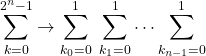
以上のことを考慮すると式(15)は
(19) ![Rendered by QuickLaTeX.com \begin{eqnarray*} &&\sum_{k=0}^{2^n-1}\frac{1}{\sqrt{2^n}}\exp{\left(i\frac{2\pi kj}{2^n}\right)} |k\rangle \\ &=&\frac{1}{\sqrt{2^n}} \sum_{k_{0}=0}^{1}\;\sum_{k_{1}=0}^{1}\cdots\sum_{k_{n-1}=0}^{1}\exp{\left(i\frac{2\pi j\sum_{l=0}^{n-1}2^{n-l-1} k_l}{2^n}\right)} |k_{0}\rangle|k_{1}\rangle\cdots|k_{n-1}\rangle \\ &=&\frac{1}{\sqrt{2^n}} \sum_{k_{0}=0}^{1}\;\sum_{k_{1}=0}^{1}\cdots\sum_{k_{n-1}=0}^{1}\exp{\left(i2\pi j\sum_{l=0}^{n-1}2^{-l-1} k_l\right)} |k_{0}\rangle|k_{1}\rangle\cdots|k_{n-1}\rangle \\ &=&\frac{1}{\sqrt{2^n}} \prod_{l=0}^{n-1}\left[\sum_{k_{l}=0}^{1}\exp{\left(i2\pi j2^{-l-1} k_l\right)} |k_{l}\rangle\right] \\ &=&\frac{1}{\sqrt{2^n}} \prod_{l=0}^{n-1}\left[|0\rangle+\exp{\left(i2\pi j2^{-l-1}\right)} |1\rangle\right] \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-03df4453f6890813ed10d81bcbba96fe_l3.png)
となる。ここで、乗積を展開するときは![]() の項が一番左側に来ると約束する。
の項が一番左側に来ると約束する。![]() についても2進数表記を行うと
についても2進数表記を行うと
(20) 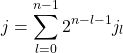
(21) 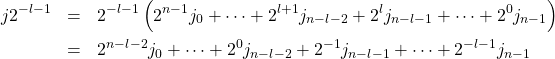
となる。右辺の先頭の![]() 個の和は正の整数である。これを整数
個の和は正の整数である。これを整数![]() に置き換え、式(21)を指数関数の肩に載せると
に置き換え、式(21)を指数関数の肩に載せると
(22) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \exp{\left(i2\pi j2^{-l-1}\right)} &=& \exp{\left(i2\pi\left[M+2^{-1}j_{n-l-1}+\cdots+2^{-l-1}j_{n-1}\right]\right)} \\ &=& \exp{\left(i2\pi\left[2^{-1}j_{n-l-1}+\cdots+2^{-l-1}j_{n-1}\right]\right)} \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-239df40dcc54d646d29f0fcf8068f44b_l3.png)
(23) ![]()
(24) ![]()
を得る。以上の結果をまとめると、式(19)は最終的に次のように変形される。
(25) ![Rendered by QuickLaTeX.com \begin{equation*} &&\sum_{k=0}^{2^n-1}\frac{1}{\sqrt{2^n}}\exp{\left(i\frac{2\pi kj}{2^n}\right)} |k\rangle= \frac{1}{\sqrt{2^n}} \prod_{l=0}^{n-1}\left[|0\rangle+\exp{\left(i2\pi0.j_{n-l-1}j_{n-l}\cdots j_{n-1} \right)} |1\rangle\right] \end{equation*}](/wp-content/ql-cache/quicklatex.com-fa24bffba4cc9b60ef3e341453a7ae6e_l3.png)
(26) ![Rendered by QuickLaTeX.com \begin{eqnarray*} F_n|j\rangle &=& \frac{1}{\sqrt{2^n}} \prod_{l=0}^{n-1}\left[|0\rangle+\exp{\left(i2\pi0.j_{n-l-1}j_{n-l}\cdots j_{n-1} \right)}|1\rangle\right] \\ &=& \frac{1}{\sqrt{2^n}}\left(|0\rangle+e^{i2\pi0.j_{n-1}}|1\rangle\right)\left(|0\rangle+e^{i2\pi0.j_{n-2}j_{n-1}}|1\rangle\right)\cdots\left(|0\rangle+e^{i2\pi 0.j_{0}j_{1}\cdots j_{n-1}}|1\rangle\right) \end{eqnarray*}](/wp-content/ql-cache/quicklatex.com-4e69ec91491306ef3cc9bb61fc81c17d_l3.png)
となる。乗積を展開するときは![]() の項が一番左側に来るように配置する。あとはこの式を量子回路で表現すれば良い。その手順を次に示す。
の項が一番左側に来るように配置する。あとはこの式を量子回路で表現すれば良い。その手順を次に示す。
QFTアルゴリズム(ステップ2)
いきなり![]() 量子ビットの場合を考えると難しいので、最初に1量子ビット、2量子ビットの場合を考える。
量子ビットの場合を考えると難しいので、最初に1量子ビット、2量子ビットの場合を考える。
QFTアルゴリズム:1量子ビットの場合
(27) ![]()
(28) ![]()
(29) 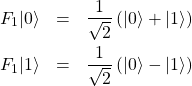
を得る。ここで、![]() を用いた。2進数
を用いた。2進数![]() は10進数で表すと
は10進数で表すと![]() であることに注意する。式(29)は先のブログで紹介したアダマールゲート
であることに注意する。式(29)は先のブログで紹介したアダマールゲート![]() で実現できる変換である。すなわち、
で実現できる変換である。すなわち、![]() である。
である。![]() の場合のQFTを実現する量子回路は下図である。
の場合のQFTを実現する量子回路は下図である。
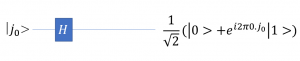
アダマールゲート![]() の行列表記は
の行列表記は
(30) ![]()
である。![]() を
を![]() と
と![]() に作用させると式(29)が得られることを確認してほしい。
に作用させると式(29)が得られることを確認してほしい。
QFTアルゴリズム:2量子ビットの場合
天下り的であるが先に2量子ビットのQFTを実現する量子回路を示す。
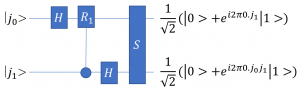
(31) ![]()
である。先頭の量子ビット![]() にアダマールゲート
にアダマールゲート![]() をかけると、
をかけると、![]() の場合のQFTの式を参考にして
の場合のQFTの式を参考にして
(32) 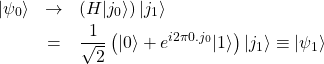
を得る。次に![]() のときだけ先頭の状態
のときだけ先頭の状態![]() に位相ゲート
に位相ゲート![]() を作用させる(このとき量子ビット
を作用させる(このとき量子ビット![]() は制御ビットと呼ばれる)。
は制御ビットと呼ばれる)。![]() は次式で定義される行列である。
は次式で定義される行列である。
(33) ![]()
この変換を丁寧に見ていく。![]() のときは何もしないので状態は
のときは何もしないので状態は![]() のままである。
のままである。![]() のときは、量子ビット
のときは、量子ビット![]() に
に![]() を作用させるので
を作用させるので
(34) 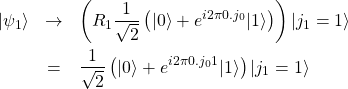
(35) ![]()
と変化することになる。この状態の後ろの量子ビット![]() にアダマールゲート
にアダマールゲート![]() をかけると
をかけると
(36) 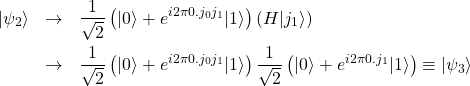
最後に、2つの量子ビットの順番を交換するSWAPゲート![]() を作用させる(今回はSWAPゲートの詳細は省略する)。
を作用させる(今回はSWAPゲートの詳細は省略する)。
(37) ![]()
最終的に得られた状態![]() は式(26)で
は式(26)で![]() としたものである。すなわち
としたものである。すなわち
(38) ![]()
である。
QFTアルゴリズム: 量子ビットの場合
量子ビットの場合
![]() の量子回路を拡張して
の量子回路を拡張して![]() の量子回路を得る。
の量子回路を得る。
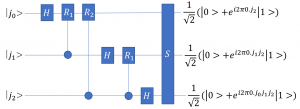
さらに、拡張すれば、一般の![]() の場合の量子回路を得る。
の場合の量子回路を得る。
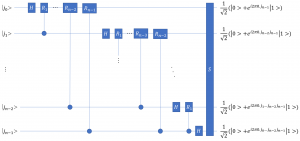
(39) ![]()
である。![]() の場合、SWAPゲート
の場合、SWAPゲート![]() によりビット列は逆順に並べ替えられる。以上で量子フーリエ変換を量子回路で表現できた。
によりビット列は逆順に並べ替えられる。以上で量子フーリエ変換を量子回路で表現できた。
古典アルゴリズム(FFT)との比較
ここでは、QFTアルゴリズムと古典アルゴリズム(FFT)の計算量の見積もりを行う。まず最初にQFTアルゴリズムから考える。量子ゲートである![]() と
と![]() の個数の和は、回路内の横線上にある四角の数を数えればよいから
の個数の和は、回路内の横線上にある四角の数を数えればよいから
(40) 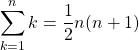
である。図の![]() で示したSWAPゲートについては今回はその詳細を説明しないが、
で示したSWAPゲートについては今回はその詳細を説明しないが、![]() 個のCNOTゲートから構成される(CNOTゲートは先のブログで紹介した)。従って、QFTアルゴリズムで使う総ゲート数は
個のCNOTゲートから構成される(CNOTゲートは先のブログで紹介した)。従って、QFTアルゴリズムで使う総ゲート数は
(41) ![]()
となる。これは![]() が大きくなると
が大きくなると![]() のオーダーで大きくなる量
のオーダーで大きくなる量![]() である。フーリエ係数の個数
である。フーリエ係数の個数![]() に換算すると
に換算すると![]() となる。これが、QFTアルゴリズムの計算量である。一方、FFTの計算量は、
となる。これが、QFTアルゴリズムの計算量である。一方、FFTの計算量は、![]() である。下図に見る通り、QFTの方が高速であることが分かる。
である。下図に見る通り、QFTの方が高速であることが分かる。
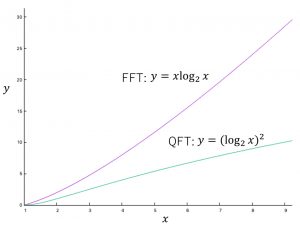
式(14)の後の文章で触れたとおり、QFTの場合、計算後に![]() 個のフーリエ係数を取り出す必要がある。この作業は指数関数的な時間を必要とするため、単にフーリエ係数を知りたいだけならFFTの方が速いというオチが付く。
個のフーリエ係数を取り出す必要がある。この作業は指数関数的な時間を必要とするため、単にフーリエ係数を知りたいだけならFFTの方が速いというオチが付く。
blueqatによる実装
今回作成したソースコードはここにある。まず最初に2量子ビットの場合のQFTを考える。このときの量子回路は以下であった。

初期状態が![]() の場合のQFTを実現するコードは以下の通り(main_2.py)。
の場合のQFTを実現するコードは以下の通り(main_2.py)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def qft_with_2qbit_00(): # |j0j1>=|00> c = Circuit(2) # j0ビットにアダマールゲートをかける。 c = c.h[0] # j1ビットを制御ビットとしてj0ビットにR1をかける。 c = c.cphase(math.pi / 2)[1, 0] # j1ビットにアダマールゲートをかける。 c = c.h[1] # 実行。 r = c.run() print("> 2qbit00") for i, v in enumerate(r): b = "{:02b}".format(i) print("[{}]{}".format(b, v)) |
コード内のコメントで示した通り、量子ゲートをひとつひとつ再現しているだけである。ただし、SWAPゲートは省略した。出力は以下の通り。
|
1 2 3 4 5 |
> 2qbit00 [00](0.4999999999999999+0j) [01](0.4999999999999999+0j) [10](0.4999999999999999+0j) [11](0.4999999999999999+0j) |
各基底状態(![]() )の係数(複素振幅)が出力される。これらは複素数である(Pythonでは虚数単位はjと表記される)。上の回路図に従って手計算を行うとすべての係数が0.5となるので(試してほしい)上の結果と一致している。
)の係数(複素振幅)が出力される。これらは複素数である(Pythonでは虚数単位はjと表記される)。上の回路図に従って手計算を行うとすべての係数が0.5となるので(試してほしい)上の結果と一致している。
次のコードは同じ2量子ビットのQFTであるが、初期状態が![]() の場合である。
の場合である。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
def qft_with_2qbit_11(): # |j0j1>=|00> c = Circuit(2) # 両ビットにXゲートをかける。Xゲートはビットを反転させる計算である。状態は|11>になる。 c = c.x[0, 1] # j0ビットにアダマールゲートをかける。 c = c.h[0] # j1ビットを制御ビットとしてj0ビットにR1をかける。 c = c.cphase(math.pi / 2)[1, 0] # j1ビットにアダマールゲートをかける。 c = c.h[1] # 実行。 r = c.run() print("> 2qbit11") for i, v in enumerate(r): b = "{:02b}".format(i) print("[{}]{}".format(b, v)) |
6行目で![]() と
と![]() の両ビットに
の両ビットに![]() ゲートを作用させている。
ゲートを作用させている。![]() ゲートはビットを反転させる量子ゲートである。
ゲートはビットを反転させる量子ゲートである。
(42) ![]()
従って、6行目で状態は![]() から
から![]() に変換される。以降の処理は先のコードと同じである。出力は以下の通り。
に変換される。以降の処理は先のコードと同じである。出力は以下の通り。
|
1 2 3 4 5 |
> 2qbit11 [00](0.4999999999999999+0j) [01](-3.0616169978683824e-17-0.4999999999999999j) [10](-0.4999999999999999+0j) [11](3.0616169978683824e-17+0.4999999999999999j) |
ここまでのコードでは、![]() までの計算しかしていない。フーリエ係数まで求めるコードは以下の通りである。
までの計算しかしていない。フーリエ係数まで求めるコードは以下の通りである。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
def qft(x): ll = len(x) lb = format(ll - 1, 'b') b = len(lb) # 状態|0>に演算子Fを作用させる。 F = Circuit() # 初期状態は|0> for i in range(b): F.h[i] for j in range(1, b - i): F.cphase(math.pi / 2**(j))[i + j, i] w = [] for j in range(ll): c = Circuit() b = format(j, 'b') bl = len(b) # Fが作用する状態|j>を作る。 for a in range(bl): if b[bl - a - 1] == '1': c = c.x[len(lb) - 1 - a] # F|j>を計算する。 # |j>を作る回路cの後ろにフーリエ変換する回路Fを結合する。 d = c + F e = d.run() # w_k,k=0,1,... w.append(e) y = [] for k in range(ll): y_k = 0 for j in range(ll): y_k += w[j][k] * x[j] y.append(y_k) return y |
このコードは一般の![]() 量子ビットの場合のQFTである。入力が
量子ビットの場合のQFTである。入力がx(![]() )、出力が
)、出力がy(![]() )である。ここで、
)である。ここで、![]() である。7行目から11行目までのコードで量子回路
である。7行目から11行目までのコードで量子回路Fを構築している。14行目から28行目までのコードで![]() の取り得るすべての状態
の取り得るすべての状態cを再現し、その各々をFに接続している(26行目:d=c+F)。31行目から35行目までの計算でフーリエ係数y_kを計算している。![]() 量子ビットの場合の量子回路を再掲しておく。
量子ビットの場合の量子回路を再掲しておく。

上で実装した関数qftを用いて次式を離散フーリエ変換してみる。
(43) ![]()
(44) ![]()
(45) 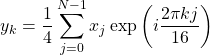
となる。この結果をqftで用いて再現してみる。
|
1 2 3 4 5 6 7 8 9 |
def fun(j): return 5.0 * np.sin(2.0 * 2.0 * np.pi * j / N) def normal_ft(k, xs): s = 0.0 for j in range(N): s += xs[j] * np.exp(complex(0, 2.0 * np.pi * k * j / N)) return s / np.sqrt(N) |
1行目の関数は式(44)を、5行目の関数は式(45)を表す。これらの式を用いて計算したフーリエ係数と、上で実装したqftによる結果とを比較する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
if __name__ == "__main__": xs = [] for i in range(N): xs.append(fun(i)) print("> Classical Fourier Transformation") for k in range(N): y = normal_ft(k, xs) v = np.abs(y) b = "{:04b}".format(k) print("[{}]{}".format(b, v)) print() print("> Quantume Fourier Transformation") ys = qft(xs) for (i, y) in enumerate(ys): v = np.abs(y) b = "{:04b}".format(i) print("[{}]{}".format(b, v)) |
ここでは、フーリエ係数の大きさ(![]() )を出力している。結果は以下の通り。
)を出力している。結果は以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
> Classical Fourier Transformation [0000]1.1102230246251565e-15 [0001]1.5895974606912448e-15 [0010]10.000000000000004 [0011]1.1430445635548515e-15 [0100]2.180278542193117e-15 [0101]2.835419185914153e-15 [0110]4.986125195590856e-15 [0111]7.795513010265399e-15 [1000]2.90236210530186e-15 [1001]8.799524318285616e-15 [1010]3.1401849173675502e-15 [1011]4.718447854656915e-15 [1100]8.253197966801011e-15 [1101]1.7997002884907162e-14 [1110]10.000000000000002 [1111]1.3011534395271244e-14 > Quantume Fourier Transformation [0000]7.771561172376096e-16 [0001]1.7554167342883505e-15 [0010]10.0 [0011]1.4936523181711914e-15 [0100]5.992897688303891e-16 [0101]1.217454592664719e-15 [0110]1.8209011484034673e-15 [0111]1.710067842969272e-15 [1000]1.2212453270876722e-15 [1001]1.807312143953211e-15 [1010]2.144196810752504e-15 [1011]1.0990647210786425e-15 [1100]3.7300332558822236e-16 [1101]2.159233940399377e-15 [1110]9.999999999999998 [1111]1.738660300550457e-15 |
どちらの結果も、0010(=2)番目と1110(=14)番目の項が10、その他の項は0となる。![]() と
と![]() だけが値を持つのは元の式
だけが値を持つのは元の式![]() が周波数2の正弦波のためである(
が周波数2の正弦波のためである(![]() は
は![]() の複素共役である)。
の複素共役である)。
まとめ
今回は、量子コンピュータを用いた計算の具体例としてフーリエ変換を取り上げ、かなり詳しく解説した(かなり長い記事になってしまった)。量子コンピュータで計算するとは、アルゴリズムを量子回路で表現することである。次回は、回帰を量子コンピュータで計算する方法を説明する予定である。

