モンティ・ホール問題

はじめに

　数学者ポール・エルデシュを描いた伝記「放浪の天才数学者エルデシュ」を最近再読しました（手元にある本は16年前に出版されてます）。この本の第6章にモンティ・ホール問題が紹介されており、天才数学者エルデシュも間違えたというエピソードが書かれています。今回は、この問題をプログラミングして数値的に解いてみます。

モンティ・ホール問題

　有名な問題です。その背景や名前の由来についてはWikipediaを見てください。ここでは問題のルールだけを示します。登場人物は司会者と解答者の二人です。最初に3つの閉じたドアが用意されます。1つのドアの向こう側には新車が置いてあり（勝ち）、他の2つにはヤギが潜んでいます（負け）。

1. 解答者がドアの1つを選択します。まだ開けません。
2. 司会者が残りの2つのドア（解答者が選んでいないドア）のうちヤギがいる方のドアを開けます。
3. この時点で閉じたドアは2つです。解答者は最初のドアのままにするか、別の閉じたドアに変えることができます。

さて、解答者が新車を獲得する確率は、ドアの選択を変えた場合と変えない場合のどちらが高くなるでしょうか？

解答

　表にすると分かり易いです。例えば解答者が最初にドア1を選んだとします。新車を獲得したら「勝ち」、ヤギだったら「負け」と呼ぶことにします。このとき、ドアの選択を変えない場合の勝敗は以下の通りです。

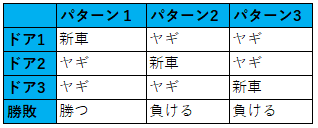
一方、解答者が選択を変える場合の勝敗は以下になります。上のルール2が存在することに注意してください。

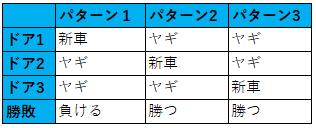
選択を変えない場合の勝つ確率（これをと書くことにします）は1/3、選択を変えた場合の勝つ確率（これをと書くことにします）は2/3です。後者の方が確率が高くなります。この問題が論争を引き起こした理由は、ルール2を見落とした、あるいは知らなかったひとが多かったからだそうです。詳細はWikipediaを見てください。

数値計算

　ソースはこちらにあります。主要部分は以下の通りです。

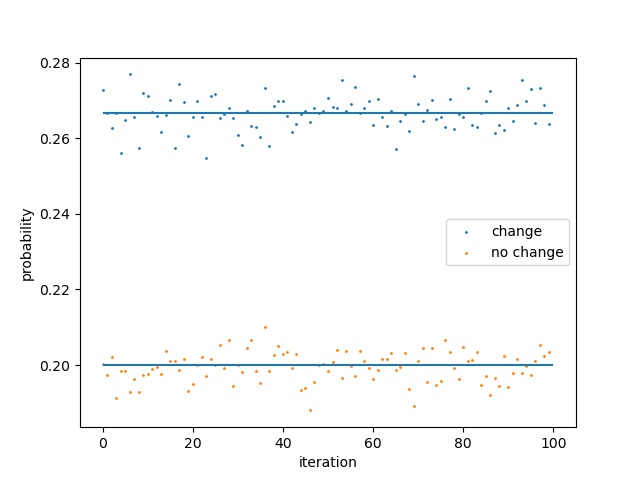
上のルールをそのままコードにしただけなので難しくありません。iterは繰り返し数です。確率を求めたいので複数回繰り返しています。iterを10000とし、この試行を100回繰り返した結果を以下に示します。

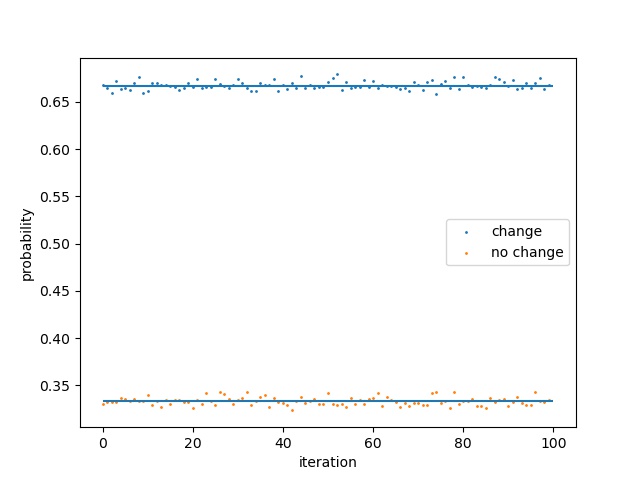
図の上の水平線は2/3を、下の水平線は1/3を表します。ほぼこれらの値を取ることが分かります。

ドアの数を増やすとどうなるか

　最後にドアの数を増やしてみます。それ以外のルールは同じです。ドアの数が4のときの結果は以下の通りです。

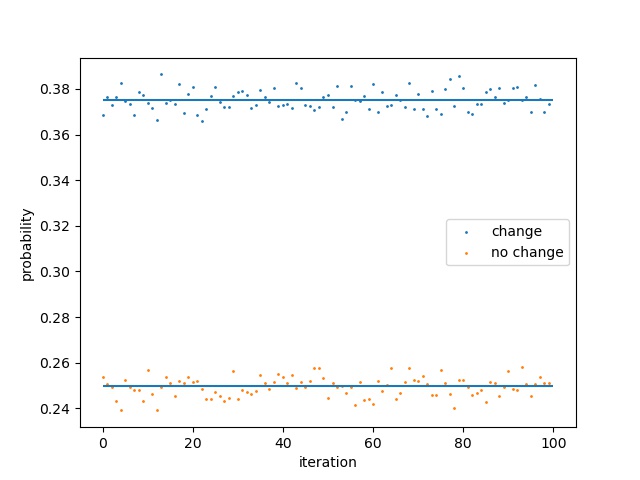
ドアの数が5のときの結果は以下の通りです。

それぞれの水平線の値は理論的に求めたものです。さて、ドアの数をとした場合の確率はいくつになるでしょうか（簡単に求まります）。ドアの数がいくつであっても最初の選択を変える方が勝つ確率は高くなります。

まとめ

　最近は昔読んだ本を掘り出して読むの日課になってます。内容は忘れているので支障はありません。今回紹介した「放浪の天才数学者エルデシュ」もそんな一冊です。モンティ・ホール問題は有名な問題なのでご存じの方も多いと思います。エルデシュ以外にも多くの数学者が間違えています。

　ところで、「エルデシュ数」なる言葉があります。エルデシュと共著論文を書いたことのある人はエルデシュ数1です。エルデシュ数1の人と共著論文を書いた人はエルデシュ数2です。女優のナタリー・ポートマンはエルデシュ数5だそうです（彼女は大学で心理学を専攻しています）。さらに調べたところ（こちらで検索できます）、私が学生のころ所属していた研究室の某教授がエルデシュ数4であることが判明しました。彼と論文を書いたことがある私のエルデシュ数はナタリー・ポートマンと同じということになります。ただし、私が論文を書いたころの某教授のエルデシュ数はだったはずなので時系列的にどうなるのかしら。まあ、いいや。