はじめに
先日、高校数学の解説動画を見ていたら「ホッケースティック恒等式」なる公式を紹介していた。初めて聞く名前であり、どうやら受験数学界隈ではたまに使われるらしいので紹介したい。
パスカルの三角形
(1) 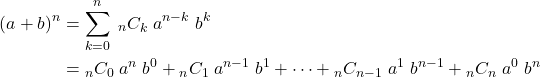
ここで![]() は
は
![]()
で定義される量であり、![]() 個から
個から![]() 個を選ぶ組み合わせの数を表す。いま式(1)の右辺の係数に注目する。
個を選ぶ組み合わせの数を表す。いま式(1)の右辺の係数に注目する。
![]()
![]() のとき
のとき
![]()
![]() のとき
のとき
![]()
![]() のとき
のとき
![]()
![]() のとき
のとき
![]()
である。この係数の組を縦に積み上げていくと次の三角形ができる。
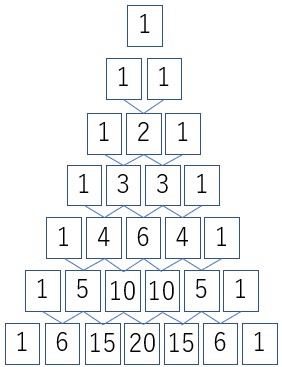
これがパスカルの三角形と呼ばれるものである。棒線で結んだ数の和がすぐ下の数となる。
ホッケースティックの恒等式
さて、パスカルの三角形の任意の場所に「ホッケースティック」を書き込む。
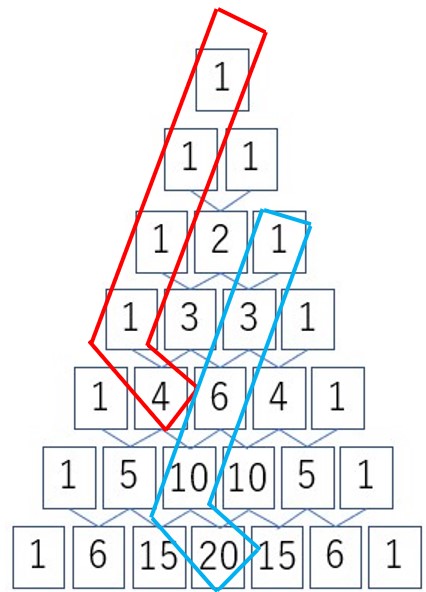
赤いスティックの場合も青いスティックの場合も、柄の部分の数の和はスティックの先の数と等しいことが分かる。どのようなスティックであってもこれは成り立つ。これが「ホッケースティック恒等式」である。一般式は以下の通り。
![]()
証明
(2) ![]()
上式を考えるため、次の問題を考える。
4個のボール(区別されない)を3人(区別される)で分けたい。ボールをもらえない人がいても良い。何通りの分け方があるか。
この種の問題には定番の解法がある。
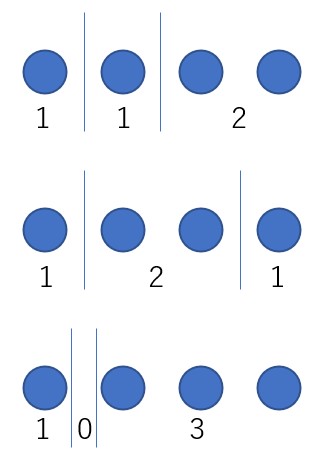
上図のように2本の棒を用意し、適当な場所にこれらを置くと1つの分け方が決まる。3人を![]() と置くと、1番上の置き方の場合は
と置くと、1番上の置き方の場合は![]() に分けられる。2番目の場合は
に分けられる。2番目の場合は![]() 、3番目の場合は
、3番目の場合は![]() である。つまり、分け方の総数は2本の棒と4個のボールを混ぜて並べた場合の並べ方の総数に等しい。
である。つまり、分け方の総数は2本の棒と4個のボールを混ぜて並べた場合の並べ方の総数に等しい。
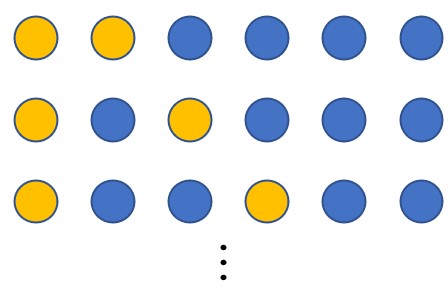
上図のように棒を橙色のボールに置き換えて6個のボールを並べれば良い。つまり、![]() 通りである。これが式(2)の左辺に相当する。同じことを見方を変えて数えることができる。最初に
通りである。これが式(2)の左辺に相当する。同じことを見方を変えて数えることができる。最初に![]() さんに0個を分けたとすると、ボールの残り4個を2人で分けることになる。これまでと同様に考えるとボール4個と棒1本を並べればよいので並べ方の総数は
さんに0個を分けたとすると、ボールの残り4個を2人で分けることになる。これまでと同様に考えるとボール4個と棒1本を並べればよいので並べ方の総数は![]() である。次に
である。次に![]() さんに1個を分けたとすると、ボールの残り3個を2人で分けることになる。ボール3個と棒1本を並べればよいので並べ方の総数は
さんに1個を分けたとすると、ボールの残り3個を2人で分けることになる。ボール3個と棒1本を並べればよいので並べ方の総数は![]() 通りである。同じことを繰り返すと
通りである。同じことを繰り返すと
 さんにボールを2個分ける場合、ボール2個と棒1本を並べればよいので
さんにボールを2個分ける場合、ボール2個と棒1本を並べればよいので 通り。
通り。 さんにボールを3個分ける場合、ボール1個と棒1本を並べればよいので
さんにボールを3個分ける場合、ボール1個と棒1本を並べればよいので 通り。
通り。 さんにボールを4個分ける場合、ボール0個と棒1本を並べればよいので
さんにボールを4個分ける場合、ボール0個と棒1本を並べればよいので 通り。
通り。
となる。これらの和が式(2)の右辺である。一般式の証明は数学的帰納法を適用すれば良いだろう(たぶん)。お時間があれば挑戦してください。
まとめ
今回は、たまたま見かけたホッケースティック恒等式を紹介した。高校数学の動画を見ていると私の知らない公式や計算テクニックがたまに出てくる。「瞬間部分積分法」や「キングプロパティ」もそうである。前者は、部分積分を繰り返し適用しないと計算できない問題を手早く処理するテクニックであり、後者は定積分の公式である。調べてみると、瞬間部分積分法は80年代の代ゼミの講師が考案したらしい。キングプロパティの方はインドや米国で使われている公式のようだ。どちらも80年代に受験生だった私は知らなかった。年代的に瞬間部分積分法の方は知っていてもおかしくないんだけど、勉強が足りなかったのかしら(でも「大学への数学」は良く買ってたんだけどなあ)。

