はじめに
数学の難問の1つに「ABC予想」と呼ばれる問題がある。最近、「宇宙際タイヒミュラー理論」を扱った論文の査読が8年間かけて終わり論文誌に掲載されることが決まったが、この理論を使うとABC予想を解くことができると言われている。今回は、このABC予想について解説したい。この予想の内容自体はそれほど難しくない。
ABC予想とは
ABC予想は1985年に提出された比較的新しい予想である。その内容は以下の通り。
(1)
を満たす、互いに素な自然数の組
に対し、
とする。このとき、任意の正の実数
に対し
(2)
となる組
は、高々有限個しか存在しない。
上の文章を読んだとき、易しくない語句は以下の3つであろう。
- 互いに素な自然数
 (根基と呼ばれる量)
(根基と呼ばれる量)- 高々有限個しか存在しない
これらを順に説明する。
互いに素な自然数
2つの自然数の組
を考える。
と
の最大公約数が1のとき、
は互いに素であると言う。
2つの自然数の組![]() の最大公約数を
の最大公約数を![]() と書くことにすれば(
と書くことにすれば(![]() はgreatest common divisorの略である)、上の主張は
はgreatest common divisorの略である)、上の主張は
(3) ![]()
と書くことができる。例えば、![]() は互いに素な自然数の組である。一方、
は互いに素な自然数の組である。一方、![]() は、
は、![]() となるので互いに素ではない。ここで、ABC予想の内容をもう一度読み返してみる。
となるので互いに素ではない。ここで、ABC予想の内容をもう一度読み返してみる。
(4)
を満たす、互いに素な自然数の組
に対し、…
3つの自然数が互いに素であると言っている。実は![]() が互いに素であれば自動的に
が互いに素であれば自動的に![]() は互いに素になる。このことは、ユークリッドの互除法を用いて証明できる。
は互いに素になる。このことは、ユークリッドの互除法を用いて証明できる。
(5) 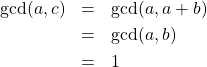
故に、![]() は互いに素である。同様に
は互いに素である。同様に
(6) 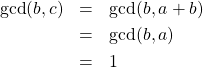
故に、![]() も互いに素である。従って、互いに素な自然数の組
も互いに素である。従って、互いに素な自然数の組![]() を選べば十分であることが分かる。
を選べば十分であることが分かる。
根基
具体例で説明する。いま、45を素因数分解する。
(7) ![]()
このとき、45の根基は以下のように計算される。
(8) ![]()
72を素因数分解すると
(9) ![]()
である。このとき、72の根基は
(10) ![]()
となる。つまり、ある自然数![]() の根基
の根基![]() とは、
とは、![]() を素因数分解した式において、全ての指数を1として計算される量である。ここでABC予想を読み返してみる。
を素因数分解した式において、全ての指数を1として計算される量である。ここでABC予想を読み返してみる。
(11)
を満たす、互いに素な自然数の組
に対し、
とする。…
ここまでは理解できた。
高々有限個しか存在しない
上の条件の下で、任意の正の実数![]() に対し
に対し
(12) ![]()
となる組![]() は「高々有限個しか存在しない」とはどういう意味なのか。これを理解するため、
は「高々有限個しか存在しない」とはどういう意味なのか。これを理解するため、![]() とした式
とした式
(13) ![]()
の場合を先に考てみる。実際に互いに素な自然数の組![]() を生成し、
を生成し、![]() を満たす組の数を数える(コードはここにある)。
を満たす組の数を数える(コードはここにある)。
| 自然数の組 |
728 | 6560 | 59048 | 1594322 |
| 2 | 4 | 6 | 13 |
それぞれの分布の様子も以下に示す。青点は生成した![]() の点を、赤点は
の点を、赤点は![]() を満たす点を表す。
を満たす点を表す。
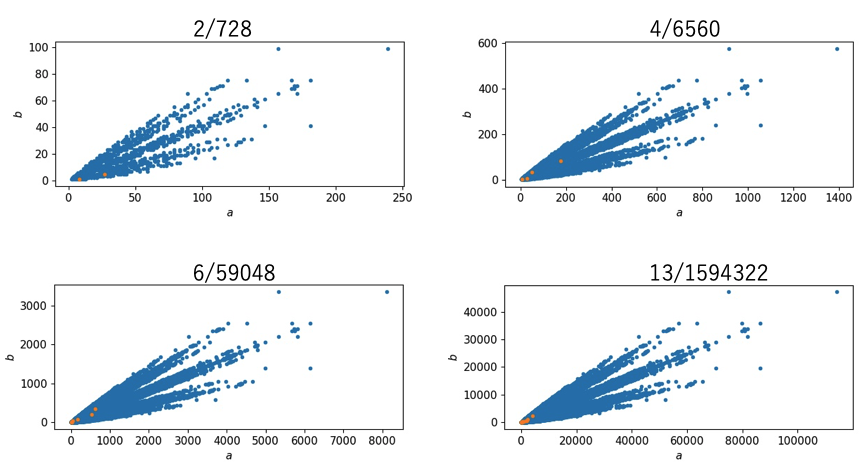
ここでは、![]() とした(このように制限しても一般性は失わない)。互いに素な自然数の組の生成方法はここに掲載されているアルゴリズムを使用した。上の表とグラフを見て分かる通り、
とした(このように制限しても一般性は失わない)。互いに素な自然数の組の生成方法はここに掲載されているアルゴリズムを使用した。上の表とグラフを見て分かる通り、![]() となる組はかなり稀である。従って、
となる組はかなり稀である。従って、![]() を満たす組は有限個に抑えられそうな印象を受けるが、実は無限個存在することが知られている。例えば
を満たす組は有限個に抑えられそうな印象を受けるが、実は無限個存在することが知られている。例えば
(14) ![]()
と置くことにより、このことを証明できる(ここに証明があります)。すなわち、![]() となる組の出現はかなりレアではあるが無限個存在するのである。しかし、
となる組の出現はかなりレアではあるが無限個存在するのである。しかし、![]() を0より大きな任意の実数とするだけで、例えそれが0.00001のような小さな数であっても、組
を0より大きな任意の実数とするだけで、例えそれが0.00001のような小さな数であっても、組![]() の数は有限個に抑えられるというのが、ABC予想の意味することである。最後にもう一度ABC予想の内容を示す。
の数は有限個に抑えられるというのが、ABC予想の意味することである。最後にもう一度ABC予想の内容を示す。
(15)
を満たす、互いに素な自然数の組
に対し、
とする。このとき、任意の正の実数
に対して、
(16)
となる組
は、高々有限個しか存在しない。
実は今回説明したABC予想は「弱い」ABC予想と呼ばれるものである。「強い」ABC予想の内容は以下の通り。
(17)
を満たす、互いに素な自然数の組
に対し、
とする。このとき、
(18)
が常に成り立つ。
冒頭に掲げた宇宙際タイヒミュラー理論が証明できるのは弱いABC予想の方である。強いABC予想が成り立つと、比較的簡単な手続きでフェルマーの定理(最終定理)を証明できる(証明はこの本にあります)。
まとめ
今回はABC予想について解説した。その内容は難しくないが、証明することは大変むずかしい問題である。これを証明できる宇宙際タイヒミュラー理論は論文誌への掲載が決まったが、世界の数学コミュニティに完全に受け入れられたわけではないことを指摘しておきたい。

