標本分散と不偏分散

はじめに

　最近、機械学習やデータ解析をしているひと達のツイッター界隈で「不偏分散はなぜn-1で割るのか」という問いが話題になっていた。私もこれまでそういうものだという認識でスルーしていたので、今回は厳密にその理由を示したい。

言葉の定義

　対象とするサンプルの全体集合を母集団と呼ぶ。例えば対象がCCTの社員の身長であれば全社員の身長が母集団である。母集団の全サンプルから計算された平均値を母平均（\mu）、母集団の全サンプルから計算された分散を母分散（\sigma^2）と言う。1つのサンプルをxで書くことにすれば次式が成り立つ。

    \begin{align*} \mu&=E[x] \\ \sigma^2&=E[(x-\mu)^2] \end{align*}

ここで、E[\cdot]は母集団における平均操作であり、期待値と呼ばれる（後述）。

　一般に、母集団に含まれる全サンプルを考えることはできないので、ランダムにサンプルを取り出すことになる。いま、N個のサンプルを取り出す場合を考え、各サンプルをx_nと書くことにすると

    \begin{align*} \bar{x}&=\dfrac{1}{N}\sum_{n=1}^{N}x_n \\ \sigma_s^2&=\dfrac{1}{N}\sum_{n=1}^{N}(x_n - \bar{x})^2 \\ \sigma_u^2&=\dfrac{1}{N-1}\sum_{n=1}^{N}(x_n - \bar{x})^2 \end{align*}

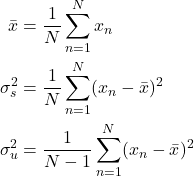
を定義することができる。\bar{x}が標本平均、\sigma_s^2が標本分散、\sigma_u^2が不偏分散（不偏標本分散）である。不偏分散が重要な理由は次式が成り立つためである。

(1)   \begin{align*} \sigma^2=E[\sigma_u^2] \end{align*}

つまり、不偏分散の期待値をとると母分散になるため、不偏分散は重要なのである。

証明

　ここでは式(1)を示す。

    \begin{align*} E[\sigma_u^2]&= E\left[\dfrac{1}{N-1}\sum_{n=1}^{N}(x_n - \bar{x})^2\right] \\ &=\frac{1}{N-1} E\left[\sum_{n=1}^{N}(x_n - \mu+\mu-\bar{x})^2\right]\\ &=\frac{1}{N-1} E\left[\sum_{n=1}^{N}\Bigl\{ (x_n - \mu)^2 +2(x_n-\mu)(\mu-\bar{x}) +(\mu-\bar{x})^2\Bigr\}\right]\\ &=\frac{1}{N-1} E\left[ \sum_{n=1}^{N} (x_n - \mu)^2 +2(\mu-\bar{x})\sum_{n=1}^{N} (x_n-\mu) +\sum_{n=1}^{N} (\mu-\bar{x})^2 \right]\\ &=\frac{1}{N-1} E\left[ \sum_{n=1}^{N} (x_n - \mu)^2 -2N(\mu-\bar{x})^2 +N(\mu-\bar{x})^2 \right] \end{align*}

ここで期待値内の第2項に

    \begin{align*} \bar{x}&=\dfrac{1}{N}\sum_{n=1}^{N}x_n \\ \end{align*}

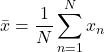
を用いた。さらに計算を進めると

    \begin{align*} E[\sigma_u^2]&= \frac{1}{N-1} E\left[ \sum_{n=1}^{N} (x_n - \mu)^2 -N(\mu-\bar{x})^2 \right]\\ &= \frac{1}{N-1}\left\{ E\left[ \sum_{n=1}^{N} (x_n - \mu)^2 \right] -NE\left[(\mu-\bar{x})^2 \right] \right\}\\ &= \frac{1}{N-1}\left\{ \sum_{n=1}^{N} E\left[(x_n - \mu)^2\right] -NE\left[(\mu-\bar{x})^2 \right] \right\} \end{align*}

となる。ここで母分散が

    \begin{align*} \sigma^2&=E[(x-\mu)^2] \end{align*}

で定義されているので

    \begin{align*} E[\sigma_u^2]= \frac{1}{N-1}\left\{ N\sigma^2 -NE\left[(\mu-\bar{x})^2 \right] \right\} \end{align*}

となる。さらに

(2)   \begin{align*} E\left[(\mu-\bar{x})^2 \right]&= E\left[\left(\frac{x_1-\mu + x_2-\mu+\cdots+x_n-\mu}{N}\right)^2 \right]\\ &=\frac{1}{N^2}E\left[\left(x_1-\mu + x_2-\mu+\cdots+x_n-\mu\right)^2 \right]\\ &=\frac{1}{N^2}\sum_{n=1}^NE\left[\left(x_n-\mu)^2 \right]\\ &=\frac{1}{N^2}\sum_{n=1}^N\sigma^2\\ &=\frac{1}{N}\sigma^2 \right] \end{align*}

が成り立つから

    \begin{align*} E[\sigma_u^2]&= \frac{1}{N-1}\left\{ N\sigma^2 -\sigma^2 \right\}\\ &=\sigma^2 \end{align*}

を得る。

補足

　式(2)の右辺2行目から3行目への変換で、和の二乗を二乗の和に変換している。これが成り立つ理由は以下のとおりである。

    \begin{align*} E\left[\left(x_1-\mu+x_2-\mu \right)^2\right]&= E\left[\left(x_1-\mu)^2+2(x_1-\mu)(x_2-\mu) +(x_2-\mu)^2 \right]\\ &=E\left[\left(x_1-\mu)^2\right] +2E\left[x_1-\mu\right]E\left[x_2-\mu\right] +E\left[(x_2-\mu)^2\right] \end{align*}

ここで

    \begin{align*} E\left[x_1-\mu\right]&=0\\ E\left[x_2-\mu\right]&=0 \end{align*}

が成り立つので

    \begin{align*} E\left[\left(x_1-\mu+x_2-\mu \right)^2\right]&=E\left[\left(x_1-\mu)^2\right] +E\left[(x_2-\mu)^2\right] \end{align*}

となる。2項以上の場合も同じである。交差項は常にゼロである。

　最後に、期待値E[\cdot]では何を計算しているのかについて触れておく。先に述べたように期待値は、母集団の全サンプルに対する平均値である。いまサンプルxが確率p(x)の割合で実現するとき量f(x)の平均値は

    \begin{align*} E\left[f(x)\right]=\int dx\;p(x)f(x) \end{align*}

で計算される。p(x)は確率であるから

    \begin{align*} 1=\int dx\;p(x) \end{align*}

が成り立っていることに注意する。今回の説明では、母集団からランダムに取り出したサンプルに番号をつけた（x_1,\cdots,x_N）。期待値を計算するときは、次のように個々のサンプル変数が積分変数になる。

    \begin{align*} E\left[f(x_n)\right]&=\int dx_n\;f(x_n)p(x_n)=\int dx\;f(x)p(x) \end{align*}

すなわち

    \begin{align*} E\left[f(x_1)\right]=E\left[f(x_2)\right]=\cdots=E\left[f(x_N)\right] \end{align*}

が成り立つ。

Pythonライブラリの分散

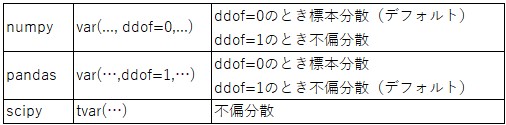
　各種Pythonライブラリが提供する分散が、標本分散なのか不偏分散なのかは注意が必要である（下の表を参照）。

まとめ

　今回は不偏分散について取り上げ、その期待値が母分散と一致することを示した。また、Pythonの各種ライブラリが提供する分散が、標本分散なのか不偏分散なのか関数名だけからは分からないことにも触れた。
　ところで、不偏分散の英語表記はunbiased varianceである。標本分散の期待値は母分散にならない（バイアスがかかっている）が、不偏分散の期待値は母分散になる（バイアスがかかっていない）、という意味のようだ（多分）。

Kumada Seiya

Kumada Seiya

仕事であろうとなかろうと勉強し続ける、その結果”中身”を知ったエンジニアになれる

最近の記事

  • 関連記事
  • おすすめ記事
  • 特集記事

アーカイブ

カテゴリー

PAGE TOP