はじめに
この数年、量子コンピュータの研究・開発が盛んである。米国のベンチャー企業の中には株式上場を行った企業もある。現在の量子コンピュータは実用化されていないが商用化されている(実用的な計算はできないがAmazonやIBMのクラウドサービスとして提供されている)という中途半端な状態にあるが、将来2000万量子ビットまで実装されれば2048ビットのRSA暗号を8時間で解くことができると主張する論文が昨年公開された。今回の記事では、このRSA暗号について解説する。量子コンピュータを用いた解法の紹介は回を改める。
RSA暗号とは
1970年代にMITの3人(Ron Rivest、Adi Shamir、Leonard Adleman)が発明した暗号手法である。彼らの名前の頭文字を取りRSA暗号と呼ばれる。暗号手順は以下の通りである。
- 最初に2つの自然数
 を決める。これを公開鍵と呼ぶ。これと対応する秘密鍵
を決める。これを公開鍵と呼ぶ。これと対応する秘密鍵 も同時に決めておく。秘密鍵は復号時に使う。
も同時に決めておく。秘密鍵は復号時に使う。 - 暗号化する文字を適当な方法で数値に置き換える。例えば、50音順を11から始まる自然数に一対一に対応させる。「あ」は11、「い」は12になる。このとき、「そすう」を数値に直すと、「そ」は25、「す」は23、「う」は13なので、これらを並べて「252313」を作る。この数を
 と置く。
と置く。  を計算し、この値を
を計算し、この値を で割った余りを
で割った余りを とする。
とする。 が暗号化された値である。
が暗号化された値である。
復号手順は以下の通りである。
- 秘密鍵
 を使い、
を使い、 を計算する。その結果を
を計算する。その結果を で割った余りが復号結果
で割った余りが復号結果 である。
である。  を元の文字列に戻す。
を元の文字列に戻す。
秘密鍵![]() を見つけるには、
を見つけるには、![]() を素因数分解する必要がある(後述)。従って、2つの巨大な素数の積として
を素因数分解する必要がある(後述)。従って、2つの巨大な素数の積として![]() を与えておけば、現在のコンピュータ(古典コンピュータ)では
を与えておけば、現在のコンピュータ(古典コンピュータ)では![]() を見つけ出すことはほぼ不可能である。以上がRSA暗号の概要である。
を見つけ出すことはほぼ不可能である。以上がRSA暗号の概要である。
次に、RSA暗号を数学的に説明するため「オイラーの定理」を紹介する。
オイラーの定理
オイラーの定理とは次のものである。
を2以上の自然数とする。1以上
以下の自然数のうち
と互いに素な(1以外の公約数を持たない)数の個数を
とする。このとき、
と互いに素な任意の自然数
に対し、
は
で割り切れる。
具体例で確認してみる。いま、![]() とする。
とする。![]() 以上
以上![]() 以下の自然数のうち
以下の自然数のうち![]() と互いに素な数は、
と互いに素な数は、![]() の
の![]() つである。従って、
つである。従って、![]() となる。
となる。![]() と互いに素な
と互いに素な![]() を選ぶと、
を選ぶと、![]() となる。これは
となる。これは![]() で割り切ることができる。従って上の定理が成り立つ。
で割り切ることができる。従って上の定理が成り立つ。
後の説明のため上の定理を合同式を用いたものに書き換えておく。
を2以上の自然数とする。1以上
以下の自然数のうち
と互いに素な(1以外の公約数を持たない)数の個数を
とする。このとき、
と互いに素な任意の自然数
に対し次式が成り立つ。
(1)
ここで、![]() とは、
とは、![]() を
を![]() で割った余りが
で割った余りが![]() であること表す。さらに、RSA暗号に使われる次の事実も紹介しておく。
であること表す。さらに、RSA暗号に使われる次の事実も紹介しておく。
を2以上の自然数とする。1以上
以下の自然数のうち
と互いに素な数を小さい順に
と並べる。これを数列
とする(常に
である)。このとき、
の中の任意の値
を数列内の全ての数に掛け、
で割った余りを並べると、数列
を並べ替えたものが得られる。
これも具体例で確認する。![]() のとき、
のとき、![]() である。
である。![]() から
から![]() を選ぶ。
を選ぶ。![]() の全ての数に2を掛けると
の全ての数に2を掛けると![]() となる。これを
となる。これを![]() で割った余りを並べると
で割った余りを並べると![]() となる。これは
となる。これは![]() を並べ替えたものである。同じことが
を並べ替えたものである。同じことが![]() 以外の数
以外の数![]() を掛けた場合も成り立つ。
を掛けた場合も成り立つ。
ここでの注目点は、![]() の中に必ず1という要素が存在することである。つまり、
の中に必ず1という要素が存在することである。つまり、![]() となるペア
となるペア![]() が必ず存在するということである。この事実を後の説明で使用する。
が必ず存在するということである。この事実を後の説明で使用する。
RSA暗号の詳細
上で紹介した定理を用いてRSA暗号を再度詳しく説明する。まず最初に2つの異なる素数![]() と
と![]() を用意し、それらの積を
を用意し、それらの積を![]() とする。実際の暗号化では巨大な素数から選ばれるので、
とする。実際の暗号化では巨大な素数から選ばれるので、![]() を素因数分解し元の素数
を素因数分解し元の素数![]() と
と![]() を求めることはほぼ不可能となる。ここでは説明の都合上、
を求めることはほぼ不可能となる。ここでは説明の都合上、![]() とする。従って、
とする。従って、![]() である。
である。![]() 以上
以上![]() 以下の自然数のうち
以下の自然数のうち![]() と互いに素な数の個数は
と互いに素な数の個数は![]() である。
である。![]() 以上
以上![]() 以下の自然数で
以下の自然数で![]() と互いに素な数の組は
と互いに素な数の組は![]() である。
である。![]() の中から適当に数
の中から適当に数![]() を選ぶ。ここでは
を選ぶ。ここでは![]() を取る。
を取る。![]() を
を![]() の全ての数に掛けると、
の全ての数に掛けると、![]() となる。これらを
となる。これらを![]() で割った余りは、
で割った余りは、![]() となる。これは
となる。これは![]() を並べ替えたものである。ここまでの議論で、
を並べ替えたものである。ここまでの議論で、![]() の2番目の要素
の2番目の要素![]() に
に![]() を掛けて
を掛けて![]() で割ると1余ることが分かる。
で割ると1余ることが分かる。
(2) ![]()
(3) ![]()
が成り立つように![]() を決めるのである。公開鍵は
を決めるのである。公開鍵は![]() 、秘密鍵は
、秘密鍵は![]() となる。
となる。
準備ができたので実際に暗号化を行う。ここでは「す」を暗号化してみる。
- 先と同じように50音順を
 から始まる自然数に割り当てると「す」は
から始まる自然数に割り当てると「す」は である。
である。  を
を で割った余りを求める。これが暗号化された値
で割った余りを求める。これが暗号化された値 になる。いまの場合、
になる。いまの場合、 を
を で割った余りなので
で割った余りなので である。合同式で書けば
である。合同式で書けば である。
である。
ここで、式(1)のオイラーの定理を考える。![]() としたから
としたから
(4) ![]()
が成り立つ。ところで
(5) ![]()
が成り立つから、両辺を![]() 乗すると
乗すると
(6) 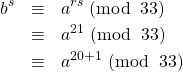
となる。ここで![]() を用いた。最後の式に
を用いた。最後の式に![]() (式(4))を使うと
(式(4))を使うと
(7) ![]()
となる。つまり、暗号化された値![]() を
を![]() 乗し
乗し![]() で割った余りを求めれば、元の値
で割った余りを求めれば、元の値![]() を得ることができる。
を得ることができる。![]() の値が式(3)を満たすように決められているので
の値が式(3)を満たすように決められているので![]() を
を![]() で割ったとき必ず1余る数であることが保証され、上の変形が成り立つのである。
で割ったとき必ず1余る数であることが保証され、上の変形が成り立つのである。
さて、公開鍵![]() から秘密鍵
から秘密鍵![]() を見破るにはどのような情報が必要になるであろうか。
を見破るにはどのような情報が必要になるであろうか。
(8) ![]()
であったから、![]() が分かれば良さそうである。しかし、
が分かれば良さそうである。しかし、![]() は
は![]() を素因数分解しない限り求めることはできない。なぜなら、
を素因数分解しない限り求めることはできない。なぜなら、![]() が成り立つからである。先に見たように実際の暗号化では
が成り立つからである。先に見たように実際の暗号化では![]() と
と![]() は巨大な素数が選択される。従って、
は巨大な素数が選択される。従って、![]() を素因数分解することは現実的にはほぼ不可能であり、従って
を素因数分解することは現実的にはほぼ不可能であり、従って![]() を求めることもできない。
を求めることもできない。
まとめ
今回は、RSA暗号について説明した。2040年ごろに2000万量子ビットが実現するだろうとDARPAが予想しているが、さてどうなるか?

