はじめに
今回は、先日話題になった![]() の新しい公式について考察してみたい。この公式はPhysical Review Lettersに掲載された超弦理論に関する論文内で紹介されている。
の新しい公式について考察してみたい。この公式はPhysical Review Lettersに掲載された超弦理論に関する論文内で紹介されている。
新しい公式
(1) 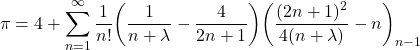
ここで、公式右辺の第二項には次のポッホハマー記号が使われている。
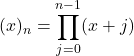
著者によると、公式(1)内の![]() は実部が-1より大きい任意の複素数で良いそうだ。
は実部が-1より大きい任意の複素数で良いそうだ。![]() を実数とし
を実数とし![]() の極限を取ると式(1)は
の極限を取ると式(1)は
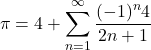
(2) 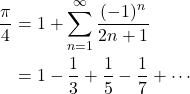
となる。これは良く知られたLeibniz(ライプニッツ)級数である。公式(1)についてのこれ以上の数学的考察は私の手に余るので、次は実際にプログラムを組んで本当に![]() に収束するのかを見てみる。
に収束するのかを見てみる。
数値計算
ソースコードはここにある。以下に結果を示す。
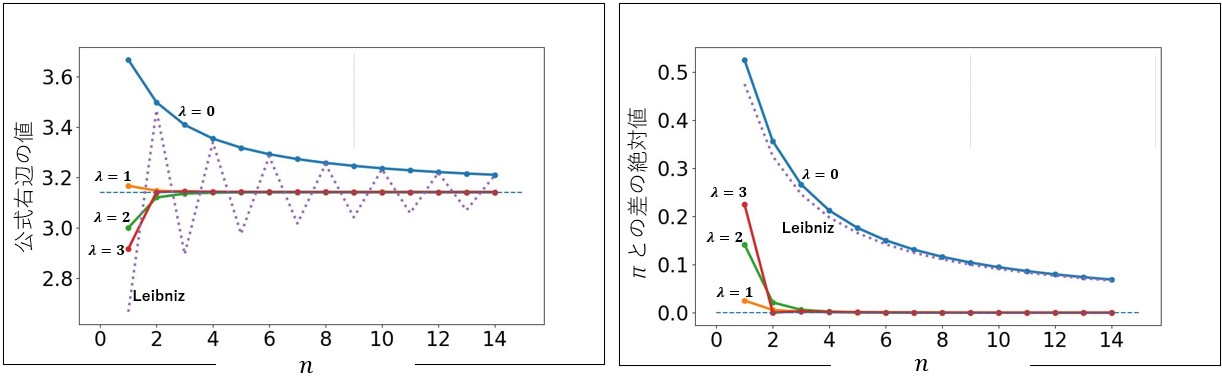
左図は公式(1)の右辺の値を縦軸に、![]() の値を横軸にしてプロットしたグラフである。
の値を横軸にしてプロットしたグラフである。![]() のときのグラフを示した。3.14近傍にある水平な破線が
のときのグラフを示した。3.14近傍にある水平な破線が![]() の値である(点線のグラフについては後述する)。これを見ると、
の値である(点線のグラフについては後述する)。これを見ると、![]() ですみやかに
ですみやかに![]() に近づいていることが分かる。右図は公式(1)の右辺と
に近づいていることが分かる。右図は公式(1)の右辺と![]() の差の絶対値を縦軸としたグラフである。この図からも
の差の絶対値を縦軸としたグラフである。この図からも![]() のとき早い段階で差分が0に近づいていることを確認できる。以下の表は上の右図のデータを表にしたものである。
のとき早い段階で差分が0に近づいていることを確認できる。以下の表は上の右図のデータを表にしたものである。
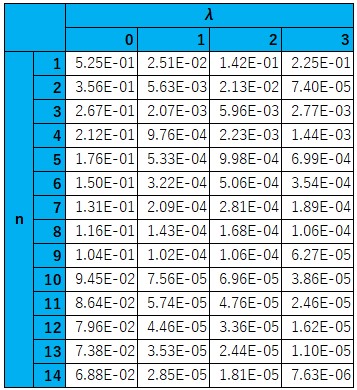
この表を見ると、![]() の値が大きくなるほど
の値が大きくなるほど![]() への収束速度も速くなっているように見える。しかし、
への収束速度も速くなっているように見える。しかし、![]() のときの公式(2)は、図の点線(Leibnizと記載したもの)のようにゆっくりと
のときの公式(2)は、図の点線(Leibnizと記載したもの)のようにゆっくりと![]() に近づいている。
に近づいている。![]() の値と収束の速さの関係を深堀りするのも面白いかもしれない(私はしないけれど)。
の値と収束の速さの関係を深堀りするのも面白いかもしれない(私はしないけれど)。
まとめ
今回は最近見かけた![]() の新しい公式を紹介し、実際に数値計算で確認してみた。著者らによると、高エネルギー粒子の振る舞いを研究している最中に、偶然
の新しい公式を紹介し、実際に数値計算で確認してみた。著者らによると、高エネルギー粒子の振る舞いを研究している最中に、偶然![]() の新しい表現方法を発見したそうである。基礎物理の研究はすぐには役には立たないけれど、研究を通して数学や物理の芳醇な世界を垣間見れることが魅力である。
の新しい表現方法を発見したそうである。基礎物理の研究はすぐには役には立たないけれど、研究を通して数学や物理の芳醇な世界を垣間見れることが魅力である。
補足
上の考察では![]() が実数の場合だけを観察した。ここでは
が実数の場合だけを観察した。ここでは![]() を複素数に拡張し、
を複素数に拡張し、![]() の場合の結果を示す。
の場合の結果を示す。![]() が複素数の場合は公式の実部を取れば良い(たぶん)。
が複素数の場合は公式の実部を取れば良い(たぶん)。
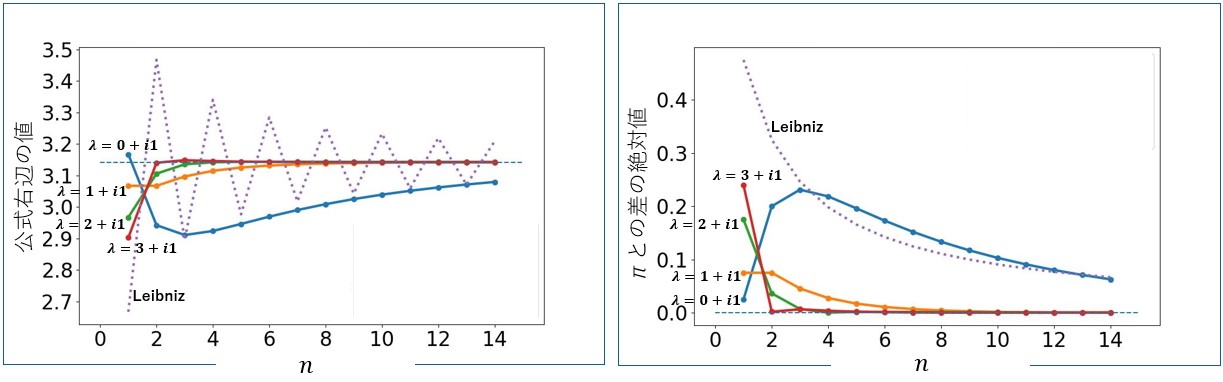
先と振る舞いが大きく異なるのは![]() の場合である。一度
の場合である。一度![]() から離れてそのあと
から離れてそのあと![]() に近づいていく。
に近づいていく。

