はじめに
今回から3回に分けて時系列解析の基礎的な話をする。話す内容は以下の3つである。
今回は、MA過程を紹介する。
定常性とホワイトノイズ
本題に入る前に「定常性」という概念を説明する。いま時系列データが以下のように与えられているとする。
![]()
(1) ![]()
ここで、![]() は
は![]() を実現する確率である。式(1)は、時刻
を実現する確率である。式(1)は、時刻![]() における
における![]() を何度も測定できると仮定した場合の平均値である。当然ながらそのような値を実際に求めることはでない。期待値は数学上の定義であることに注意する。次に、時間差
を何度も測定できると仮定した場合の平均値である。当然ながらそのような値を実際に求めることはでない。期待値は数学上の定義であることに注意する。次に、時間差![]() の自己共分散を次式で定義する。
の自己共分散を次式で定義する。
(2) ![]()
式(1)の期待値が時刻に依存せず(![]() )、式(2)の自己共分散が時間差
)、式(2)の自己共分散が時間差![]() のみに依存するとき(
のみに依存するとき(![]() )、その時系列データは定常性を持つと言う。まとめると以下になる。
)、その時系列データは定常性を持つと言う。まとめると以下になる。
![]()
ここで、![]() と
と![]() は時間に依存しない量である。
は時間に依存しない量である。
次に、ホワイトノイズ(White Noise:W.N.)を定義する。
![Rendered by QuickLaTeX.com \begin{align*} &\mu={\rm E}[\epsilon_t]=0\\ &\gamma_k={\rm E}[\epsilon_t\epsilon_{t-k}]= \left\{ \begin{array}{l} \sigma^2,\; k=0 \\ 0, \;\;\;k\neq 0 \end{array} \right. \end{align*}](/wp-content/ql-cache/quicklatex.com-8598d79c59480fc0f99652ef844a8e57_l3.png)
上が成り立つとき、時系列データ![]() をホワイトノイズと呼ぶ。
をホワイトノイズと呼ぶ。![]() はホワイトノイズの分散である。ホワイトノイズの隣接時刻間(
はホワイトノイズの分散である。ホワイトノイズの隣接時刻間(![]() )の自己共分散は0である。また、ホワイトノイズは定常性を持つことも分かる。
)の自己共分散は0である。また、ホワイトノイズは定常性を持つことも分かる。
MA(1)過程
我々が実世界で扱う時系列データは多くの場合、自己相関を持つ。ここで自己相関とは異なる時刻における値![]() と
と![]() が何らかの関係を持つことである(厳密な定義は後述する)。この自己相関を表現できる最も簡単なモデルが1次のMA過程(MA(1)過程)である。名前にあるMAとはMoving Averageの略である(この名前の由来については後で触れる)。MA(1)過程は次式で定義される。
が何らかの関係を持つことである(厳密な定義は後述する)。この自己相関を表現できる最も簡単なモデルが1次のMA過程(MA(1)過程)である。名前にあるMAとはMoving Averageの略である(この名前の由来については後で触れる)。MA(1)過程は次式で定義される。
![]()
ここで、![]() は分散
は分散![]() のホワイトノイズ、
のホワイトノイズ、![]() と
と![]() は任意の実数値を取る定数である。図1は
は任意の実数値を取る定数である。図1は![]() の値を変化させたとき(それ以外の定数は固定)の時系列データの様子である(コードはここにある)。
の値を変化させたとき(それ以外の定数は固定)の時系列データの様子である(コードはここにある)。
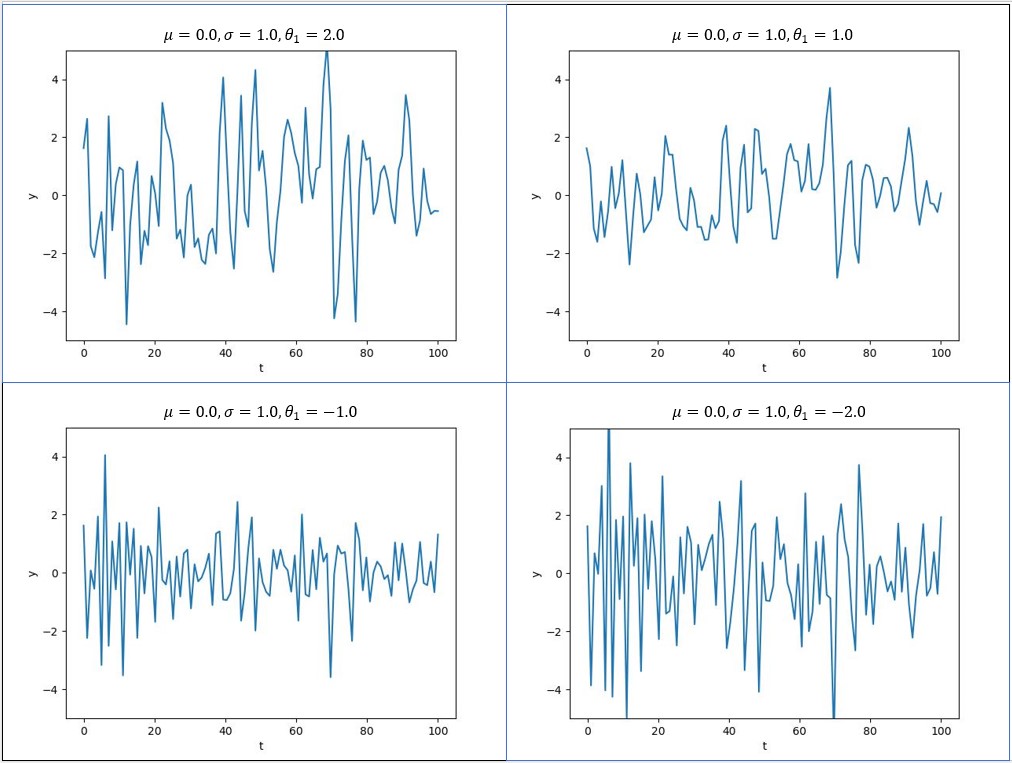
図1
![]()
となり、両方に![]() が含まれていることが分かる。従って、
が含まれていることが分かる。従って、![]() が負の場合、
が負の場合、![]() と
と![]() の変位の向きが逆になる傾向が強くなり振動が激しくなる。このことは上のグラフで確認することができる。
の変位の向きが逆になる傾向が強くなり振動が激しくなる。このことは上のグラフで確認することができる。
さて、MA(1)過程の期待値は次式となる。
![]()
ここで、ホワイトノイズの定義を用いた。さらに、MA(1)過程の自己共分散は次式となる。
![Rendered by QuickLaTeX.com \begin{align*} \gamma_k &={\rm Cov}[y_t,y_{t-k}]\\ &={\rm E}[(y_t-\mu)(y_{t-k}-\mu)]\\ &={\rm E}[\epsilon_t\epsilon_{t-k}]+\theta_1{\rm E}[\epsilon_t\epsilon_{t-k-1}]+\theta_1{\rm E}[\epsilon_{t-1}\epsilon_{t-k}]+\theta_1^2{\rm E}[\epsilon_{t-1}\epsilon_{t-k-1}] \end{align*}](/wp-content/ql-cache/quicklatex.com-926d3c95b37919f82fb52a7f8be25713_l3.png)
ホワイトノイズの定義を使えば以下を得る。
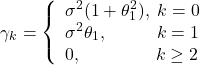
1次のMA過程では![]() のとき常に
のとき常に![]() である。つまり、時刻の間が2以上離れると共分散は0になる。さらに、
である。つまり、時刻の間が2以上離れると共分散は0になる。さらに、![]() 次の自己相関
次の自己相関![]() が次式で定義される。
が次式で定義される。
![]()
従って、MA(1)の1次の自己相関は
![]()
となる。下のグラフは![]() を
を![]() のグラフとして描いたものである。
のグラフとして描いたものである。
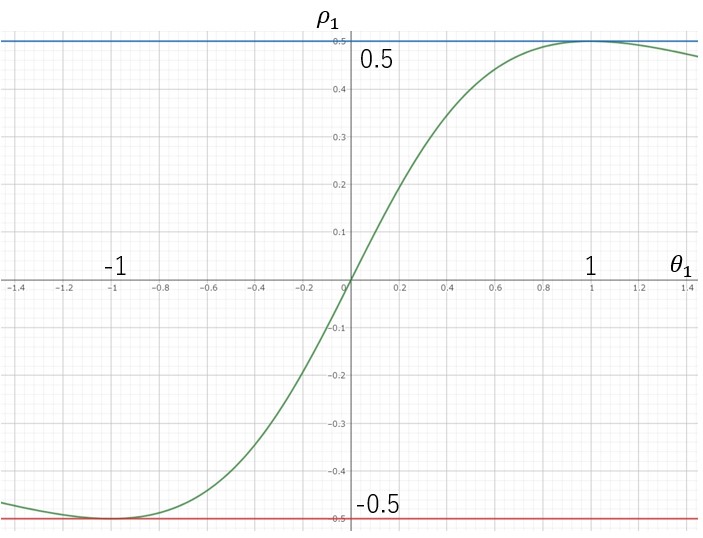
図2
上のグラフから![]() でそれぞれ最小値(-1/2)と最大値(1/2)を持つことが分かる。見方を変えれば、MA(1)過程は大きさ1/2以上の相関を表すことができないモデルである。MA(1)過程の性質をまとめると以下になる。
でそれぞれ最小値(-1/2)と最大値(1/2)を持つことが分かる。見方を変えれば、MA(1)過程は大きさ1/2以上の相関を表すことができないモデルである。MA(1)過程の性質をまとめると以下になる。
![Rendered by QuickLaTeX.com \begin{align*} &{\rm E}[y_t]=\mu\\ &\gamma_0=\sigma^2(1+\theta_1^2)\\ &\gamma_k= \left\{ \begin{array}{l} \sigma^2\theta_1,\;\;\;\;\;\;\;\;\;\;k=1\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k\geq 2 \end{array} \right.\\ &\rho_k= \left\{ \begin{array}{l} \frac{\theta_1}{1+\theta_1^2},\;\;\;\;\;\;\;\;\;\;k=1\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k\geq 2 \end{array} \right. \end{align*}](/wp-content/ql-cache/quicklatex.com-76ce2f9cf90d36d25a9cabb4ba692199_l3.png)
MA(q)過程
上のMA(1)過程は容易にMA(![]() )過程に拡張することができる。MA(
)過程に拡張することができる。MA(![]() )過程は次式で定義される。
)過程は次式で定義される。
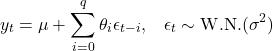
ただし、![]() とした。その性質は以下になる。
とした。その性質は以下になる。
![Rendered by QuickLaTeX.com \begin{align*} &{\rm E}[y_t]=\mu\\ &\gamma_0=\sigma^2\sum_{i=0}^q\theta_i^2\\ &\gamma_k= \left\{ \begin{array}{l} \sigma^2\sum_{i=0}^{q-k}\theta_{i}\theta_{k+i},\;\;\;1\leq k \leq q\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k\geq q+1 \end{array} \right.\\ &\rho_k= \left\{ \begin{array}{l} \frac{\sum_{i=0}^{q-k}\theta_{i}\theta_{k+i}}{\sum_{i=0}^q\theta_i^2},\;\;\;\;\;\;\;\;\;\;1\leq k \leq q\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k\geq q+1 \end{array} \right. \end{align*}](/wp-content/ql-cache/quicklatex.com-f345f61e3fc5f7da3ba1f352dfeee2ee_l3.png)
ここで大切なことは、MA(![]() )過程の相関
)過程の相関![]() は
は![]() 次以降で0になることである。言い換えれば
次以降で0になることである。言い換えれば![]() 次の自己相関をモデル化するには
次の自己相関をモデル化するには![]() 個のパラメータが必要となる。長時間に渡る相関をモデル化する際に多くのパラメータを必要とする点がMA(
個のパラメータが必要となる。長時間に渡る相関をモデル化する際に多くのパラメータを必要とする点がMA(![]() )過程の欠点である。
)過程の欠点である。
さて、MA(![]() )過程のMAはMoving Average(移動平均)の略であることを上で述べた。移動平均と呼ぶ理由を以下に述べる。MA(
)過程のMAはMoving Average(移動平均)の略であることを上で述べた。移動平均と呼ぶ理由を以下に述べる。MA(![]() )過程は次式で与えられた。
)過程は次式で与えられた。
(3) 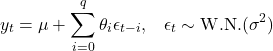
ここで、右辺第2項はホワイトノイズに重み付けを行い和を取っていると解釈できる。すなわち![]() の幅の窓の中で平均(厳密には平均ではないが)を計算しているとみなすことができる。これが移動平均と言う名前が付いた理由である。
の幅の窓の中で平均(厳密には平均ではないが)を計算しているとみなすことができる。これが移動平均と言う名前が付いた理由である。
MA過程の長所と短所
MA過程の長所と短所を以下にまとめる。
長所
短所
まとめ
今回は、時系列データを表現する最も簡単な過程であるMA過程を紹介した。これはホワイトノイズの線形和として定義されるものである。 MA(![]() )過程では
)過程では![]() 次までの自己相関をモデル化でき、必要とされるパラメータの数も
次までの自己相関をモデル化でき、必要とされるパラメータの数も![]() 個となることを見た。自己相関が長時間になるほど多くのパラメータを扱わなければならないことがこの過程の欠点である。次回は別の手法で自己相関を表現する方法を紹介する。
個となることを見た。自己相関が長時間になるほど多くのパラメータを扱わなければならないことがこの過程の欠点である。次回は別の手法で自己相関を表現する方法を紹介する。

