はじめに
先の解説でConditional Variational Autoencoder(CVAE)を取り上げ、画像を生成するモデルを例として考えた。そのとき扱った画像はMNISTデータセットである。このデータセットの画像を2値画像であるとみなし、0と1を生成するベルヌーイ分布を導入した。実は、MNISTの画像は2値画像ではなく、グレイ画像である。今回の記事では、連続値を生成する確率分布(ガウス分布)を用いてグレイ画像をまじめに扱う。本記事では簡単のため、Conditionalではない普通のVariational Autoencoder(VAE)を用いて画像生成モデルを学習する。
ベイズの変分推論
最初にVAEを定式化する。観測値を![]() とし、潜在変数
とし、潜在変数![]() を考え、これら2つの同時確率分布
を考え、これら2つの同時確率分布![]() にベイズの定理を適用する。
にベイズの定理を適用する。
(1) ![]()
事後確率![]() をベイズの変分推論により求める。
をベイズの変分推論により求める。![]() を近似する関数としてパラメータ
を近似する関数としてパラメータ![]() を持つ関数
を持つ関数![]() を導入し、次のKullback-Leibler Divergenceを最小にする。
を導入し、次のKullback-Leibler Divergenceを最小にする。
(2) ![]()
(3) ![]()
となる。ここで、![]() は
は![]() についての期待値を表す。右辺の第3項は
についての期待値を表す。右辺の第3項は![]() に依存しないので、右辺を
に依存しないので、右辺を![]() について最小にするには次式を最小にすれば良い。
について最小にするには次式を最小にすれば良い。
(4) ![]()
ところで、![]() を用いて式(3)を変形すると
を用いて式(3)を変形すると
(5) ![]()
を得る。Kullback-Leibler Divergenceは常に0以上であるから
(6) ![]()
となる。左辺の量![]() はEvidenceと呼ばれる量であり、この対数の下限が
はEvidenceと呼ばれる量であり、この対数の下限が![]() であることを上式は示している。この下限をEvidence Lower Bound(ELBO)と呼ぶ。すなわち、ELBOを最大することと、
であることを上式は示している。この下限をEvidence Lower Bound(ELBO)と呼ぶ。すなわち、ELBOを最大することと、![]() を最小にすることとは等価である。いずれにせよ、式(4)を最小するような
を最小にすることとは等価である。いずれにせよ、式(4)を最小するような![]() を見つけることが目標になる。
を見つけることが目標になる。
深層生成モデル
確率分布![]() を正規分布で表し、そのパラメータである平均
を正規分布で表し、そのパラメータである平均![]() と分散
と分散![]() をネットワークを用いて計算する。
をネットワークを用いて計算する。
(7) ![]()
ここで、![]() は
は![]() の関数であり、パラメータ
の関数であり、パラメータ![]() はネットワークの各種重みに相当する。ネットワークを用いて表現された生成モデルを深層生成モデルと呼ぶ。本記事では
はネットワークの各種重みに相当する。ネットワークを用いて表現された生成モデルを深層生成モデルと呼ぶ。本記事では![]() がグレイ画像の場合を考える。グレイ画像の画素は、0から255までのいずれかの整数値を持つ。従って、
がグレイ画像の場合を考える。グレイ画像の画素は、0から255までのいずれかの整数値を持つ。従って、![]() として仮定できる確率分布は、255種類の離散値を生成できるものでなければならない。真っ先に思いつくのがカテゴリカル分布である。しかし、実際にこれを用いて計算を行ったところ訓練に大変時間がかかることが分かった。そこで、画素値を255で割り0から1までの実数値に変換した。このようにすれば、任意の実数値を生成できるガウス分布を用いることができる。
として仮定できる確率分布は、255種類の離散値を生成できるものでなければならない。真っ先に思いつくのがカテゴリカル分布である。しかし、実際にこれを用いて計算を行ったところ訓練に大変時間がかかることが分かった。そこで、画素値を255で割り0から1までの実数値に変換した。このようにすれば、任意の実数値を生成できるガウス分布を用いることができる。
(8) 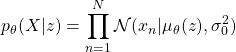
パラメータ![]() は、入力を
は、入力を![]() とするネットワークで計算される。
とするネットワークで計算される。![]() はネットワークの重みを表す。今回の計算では分散
はネットワークの重みを表す。今回の計算では分散![]() は定数(ハイパーパラメータ)とした。これもネットワークで決める計算を行ってみたが、損失関数の減衰が不安定であった。最後に、
は定数(ハイパーパラメータ)とした。これもネットワークで決める計算を行ってみたが、損失関数の減衰が不安定であった。最後に、![]() として次の標準正規分布を仮定した。
として次の標準正規分布を仮定した。
(9) ![]()
ここまでの様子を図にすると以下のようになる。
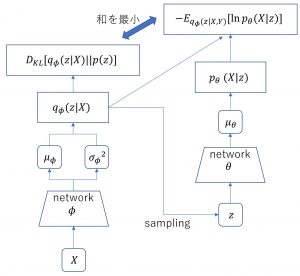
図1. VAEの処理の流れ
結果
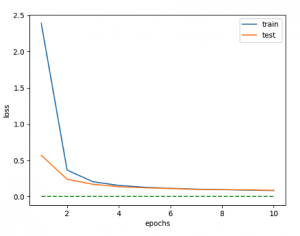
今回もPixyzを用いて実装し、データセットとしてModelNet40を用いた。このデータセットが持つ3Dモデルをさまざまな角度から見た距離画像(グレイ画像)を作成し、これを訓練画像とした。画像枚数はおおよそ9万8千枚である。最初に、訓練時の損失関数の減衰の様子を示す。ハイパーパラメータ![]() を0.01とした。
を0.01とした。
次に、再構成画像を示す。再構成画像とは上の図1で、![]() を入力したときの
を入力したときの![]() が生成する画像のことである。この画像が
が生成する画像のことである。この画像が![]() と似てるほどVAEの精度は良い。
と似てるほどVAEの精度は良い。

物体の形状と濃淡を完全ではないが再現できていることが分かる。最後に、標準正規分布から発生させた乱数から生成した画像を示す。これは図1の右段だけの処理である。

生成画像については残念な結果になった。何が描画されているのか分からない。もう少し、損失値を減らす工夫が必要そうである。
まとめ
今回は、グレイ画像を生成するVAEを考察した。VAEのサンプルコードをGoogleで検索してもベルヌーイ分布を用いたものしか見つからない。グレイ画像は2値画像ではないからベルヌーイ分布は不適切である。今回の記事では、ガウス分布を導入することでグレイ画像を扱えることを示した。ただし、乱数からの画像生成についてはもう少し丁寧な議論が必要である。

