はじめに
こんにちは。よっしーです。
前回の記事ではモンテカルロシミュレーションというシミュレーション手法を紹介しました。
今回はそれを用いて確率に ![]() が出現するような面白い事象を紹介したいと思います。
が出現するような面白い事象を紹介したいと思います。
確率に円周率が出てくると言うのは日常生活ではなかなか考えづらいので一つの知識として知っておいていただけますと幸いです。
ビュフォンの針
多数の平行線を引き、そこに針を落とした時、いづれかの線と針が交差する確率はいくつか。
こちらはジョルジュ=ルイ・ルクレール・ド・ビュフォンが提示した「ビュフォンの針の問題」と言われている問題です。
事象としては図を見たほうが分かりやすいので図を載せます。
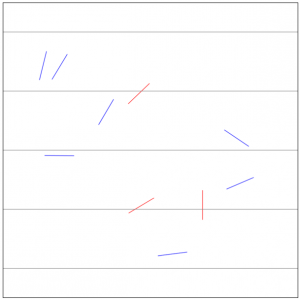
5 本の線(外枠を除くグレーの横線)と針(赤線と青線)を描画してみました。
赤線は平行線と交差した針、青線は平行線と交差していない針を表現しています。
10 本中 3 本が平行線と交差していることが分かります。
ところで、針と線が交わる確率は針の長さと平行線の間隔で決まります。
なぜなら、とてつもなく長い針を用いたり、極端に狭い幅の平行線だとすぐに針が平行線に触れてしまうからです。(短い針、間隔が広い場合も同様です)
針が長く幅が狭い場合

針が短く幅が広い場合

上図の 2 つでは確率に差が出ますので、それも考慮して確率を考えていく必要があります。
ここで、以前行ったモンテカルロシミュレーションを使えば、確率計算せずとも色々なシチュエーションで確率を求めることができます。
実際にシミュレーションしてみる
実際にシミュレーションしてみましょう。
今後、針の長さを![]() , 平行線の幅を
, 平行線の幅を![]() と置きます。
と置きます。
![]() ,
, ![]() で試してみます。
で試してみます。
10000 本の針を落としてみました。
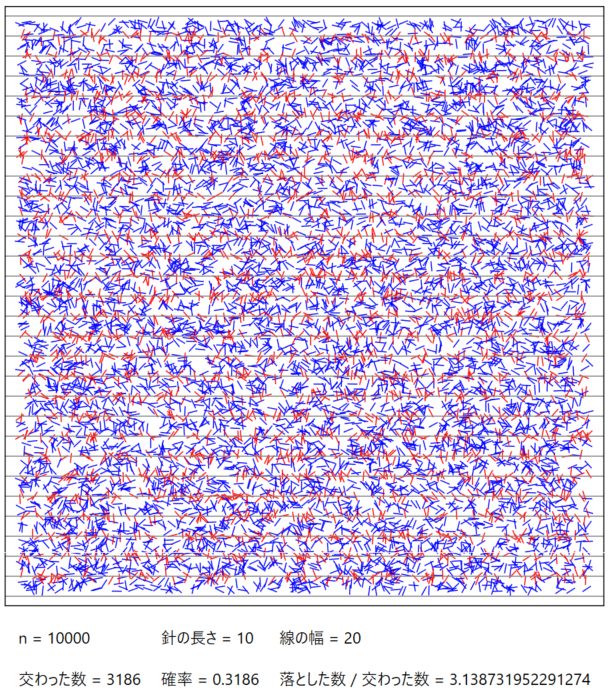
10000 本中 3186 本平行線と交差したので確率は 0.3186 でした。
逆に、何本に 1 本の割合で平行線にヒットしたかを考えると 3.1387…でした。
これは確率の逆数を取ったと言えます。
どこか見覚えのある数字の気がする。
そうです。これこそが円周率 ![]() なのです。
なのです。
回数を増やして見てみますと以下のようになります。
結果は以下となりました。
| 試行回数 | 交差した本数 | 確率 | 確率の逆数 |
|---|---|---|---|
| 10000 | 3186 | 0.3186 | 3.1387 |
| 1000000 | 317980 | 0.3180 | 3.145 |
| 100000000 | 3184038 | 0.3184 | 3.1407 |
このことをまとめると![]() ,
, ![]() の時、確率
の時、確率 ![]() は
は
![]()
となることが分かります。
ここで、![]() や
や ![]() を変更してしてみて、1000000 回試行してみます。
を変更してしてみて、1000000 回試行してみます。
両方一度に変えるとややこしいので ![]() のみ変えてみます。
のみ変えてみます。
| l | d | 交差した本数 | 確率 | 確率の逆数 |
|---|---|---|---|---|
| 2.5 | 20 | 79649 | 0.0796 | 12.5551 |
| 5 | 20 | 158908 | 0.1589 | 6.2929 |
| 7.5 | 20 | 238626 | 0.2386 | 4.1907 |
| 10 | 20 | 317980 | 0.3180 | 3.1449 |
| 12.5 | 20 | 398002 | 0.398 | 2.5126 |
| 15 | 20 | 477211 | 0.4772 | 2.0955 |
| 17.5 | 20 | 556991 | 0.557 | 1.7954 |
| 20 | 20 | 636654 | 0.6367 | 1.5707 |
| 22.5 | 20 | 691036 | 0.691 | 1.4471 |
| 25 | 20 | 727357 | 0.7274 | 1.3748 |
| 27.5 | 20 | 756181 | 0.7562 | 1.3224 |
| 30 | 20 | 778936 | 0.7789 | 1.2838 |
| 32.5 | 20 | 796710 | 0.7967 | 1.2552 |
| 35 | 20 | 812240 | 0.8122 | 1.2312 |
| 37.5 | 20 | 825567 | 0.8256 | 1.2113 |
| 40 | 20 | 837685 | 0.8377 | 1.1938 |
![]() で固定した時の
で固定した時の ![]() と確率
と確率![]() の関係は以下のようです。
の関係は以下のようです。
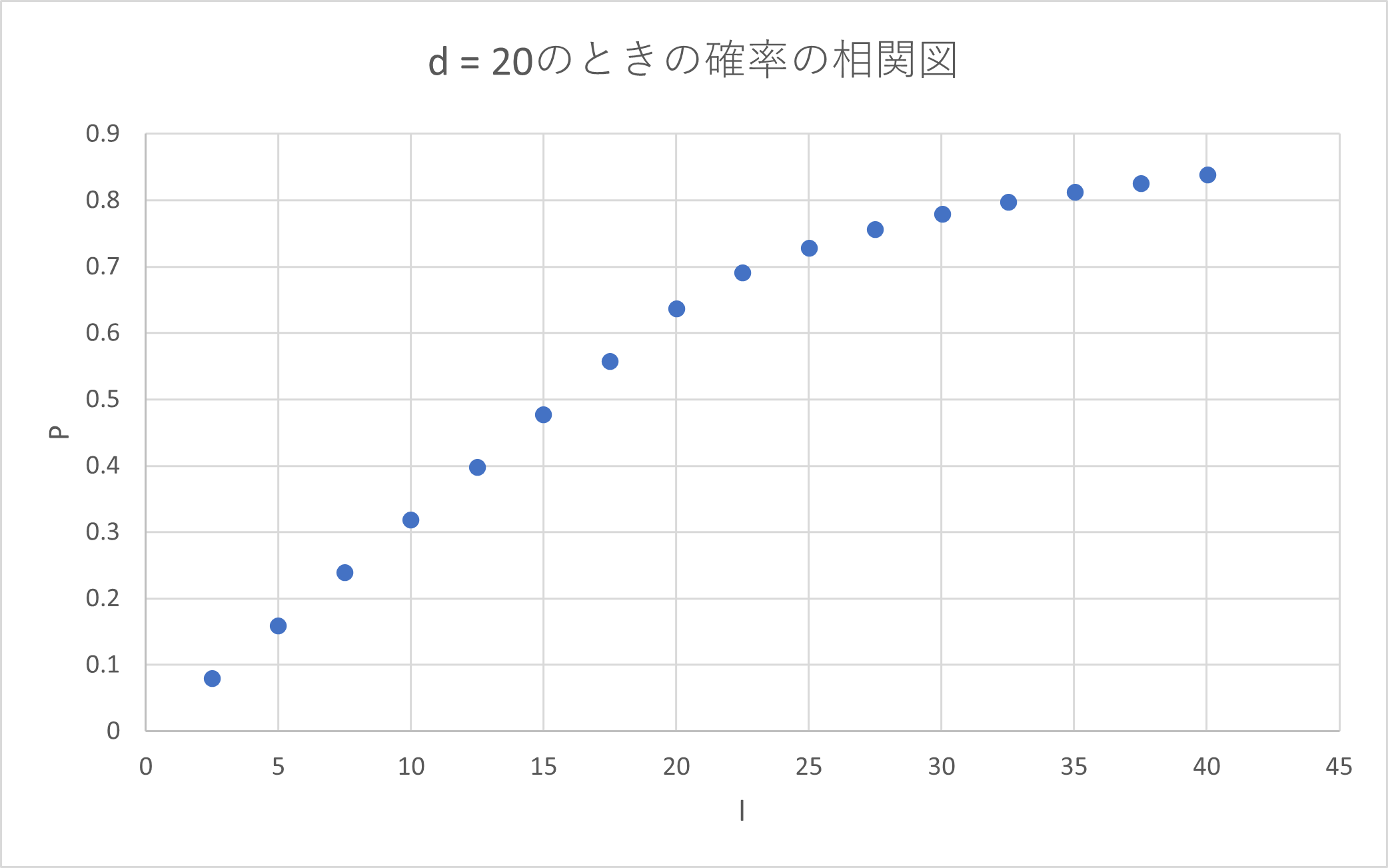
![]() が 20 になるまではグラフが比例しているように見えます。
が 20 になるまではグラフが比例しているように見えます。
![]() の場合と
の場合と ![]() の場合で関係性が違いそうです。
の場合で関係性が違いそうです。
![]() の場合は複雑なので、
の場合は複雑なので、![]() の場合を考えると、
の場合を考えると、
![]()
と置いておきます。
上記の関係性を裏付けるために ![]() の時を見てみると、
の時を見てみると、
| l | d | 交差した本数 | 確率 | 確率の逆数 |
|---|---|---|---|---|
| 2.5 | 30 | 53343 | 0.0533 | 18.7466 |
| 5 | 30 | 106089 | 0.1061 | 9.4260 |
| 7.5 | 30 | 159141 | 0.1591 | 6.2837 |
| 10 | 30 | 212292 | 0.2123 | 4.7105 |
| 12.5 | 30 | 264526 | 0.2645 | 3.7803 |
| 15 | 30 | 317836 | 0.3178 | 3.1463 |
| 17.5 | 30 | 371694 | 0.3717 | 2.6904 |
| 20 | 30 | 423372 | 0.4234 | 2.3620 |
| 22.5 | 30 | 476238 | 0.4762 | 2.0998 |
| 25 | 30 | 530611 | 0.5306 | 1.8846 |
| 27.5 | 30 | 584066 | 0.5841 | 1.7121 |
| 30 | 30 | 636691 | 0.6367 | 1.5706 |
| 32.5 | 30 | 675306 | 0.6753 | 1.4808 |
| 35 | 30 | 704432 | 0.7044 | 1.4196 |
| 37.5 | 30 | 728430 | 0.7284 | 1.3728 |
| 40 | 30 | 747569 | 0.7476 | 1.3377 |
| 42.5 | 30 | 763607 | 0.7636 | 1.3096 |
| 45 | 30 | 778750 | 0.7788 | 1.2841 |
| 47.5 | 30 | 791145 | 0.7911 | 1.2640 |
| 50 | 30 | 803157 | 0.8032 | 1.2451 |
| 52.5 | 30 | 812986 | 0.8130 | 1.2300 |
| 55 | 30 | 821634 | 0.8216 | 1.2171 |
| 57.5 | 30 | 830030 | 0.8300 | 1.2048 |
| 60 | 30 | 837049 | 0.8370 | 1.1947 |
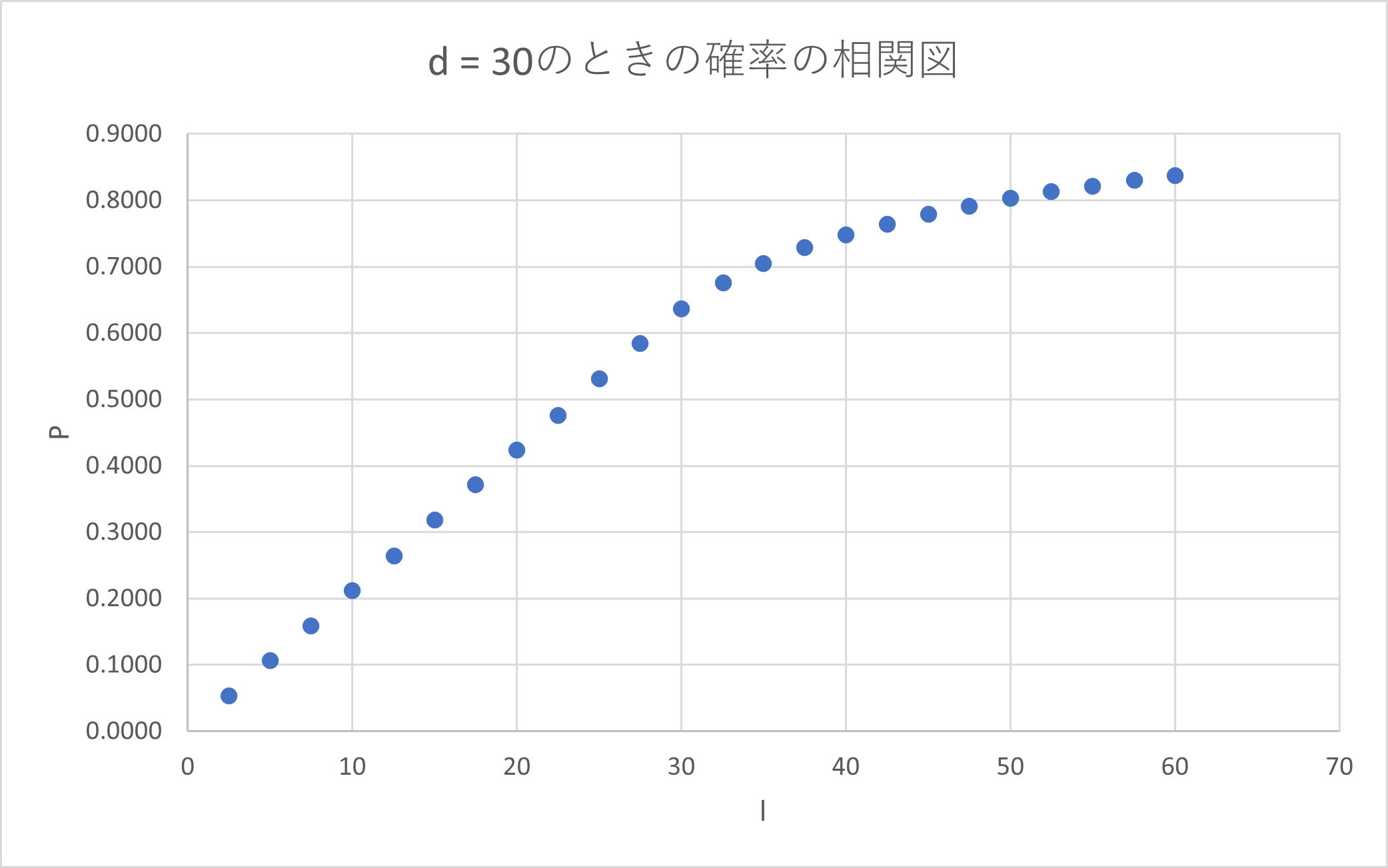
![]() の時の関係と一致していそうです。
の時の関係と一致していそうです。
今度は![]() を固定して、
を固定して、![]() を変化させてみましょう。
を変化させてみましょう。
| l | d | 交差した本数 | 確率 | 確率の逆数 |
|---|---|---|---|---|
| 10 | 2 | 936056 | 0.9361 | 1.0683 |
| 10 | 4 | 870416 | 0.8704 | 1.1489 dfrac |
| 10 | 6 | 802577 | 0.8026 | 1.2460 |
| 10 | 8 | 727014 | 0.7270 | 1.3755 |
| 10 | 10 | 636667 | 0.6367 | 1.5707 |
| 10 | 12 | 530250 | 0.5303 | 1.8859 |
| 10 | 14 | 448384 | 0.4484 | 2.2302 |
| 10 | 16 | 389057 | 0.3891 | 2.5703 |
| 10 | 18 | 345457 | 0.3455 | 2.8947 |
| 10 | 20 | 317980 | 0.3180 | 3.1449 |
![]() で固定した時の
で固定した時の ![]() と確率
と確率 ![]() の関係は以下のようです。
の関係は以下のようです。
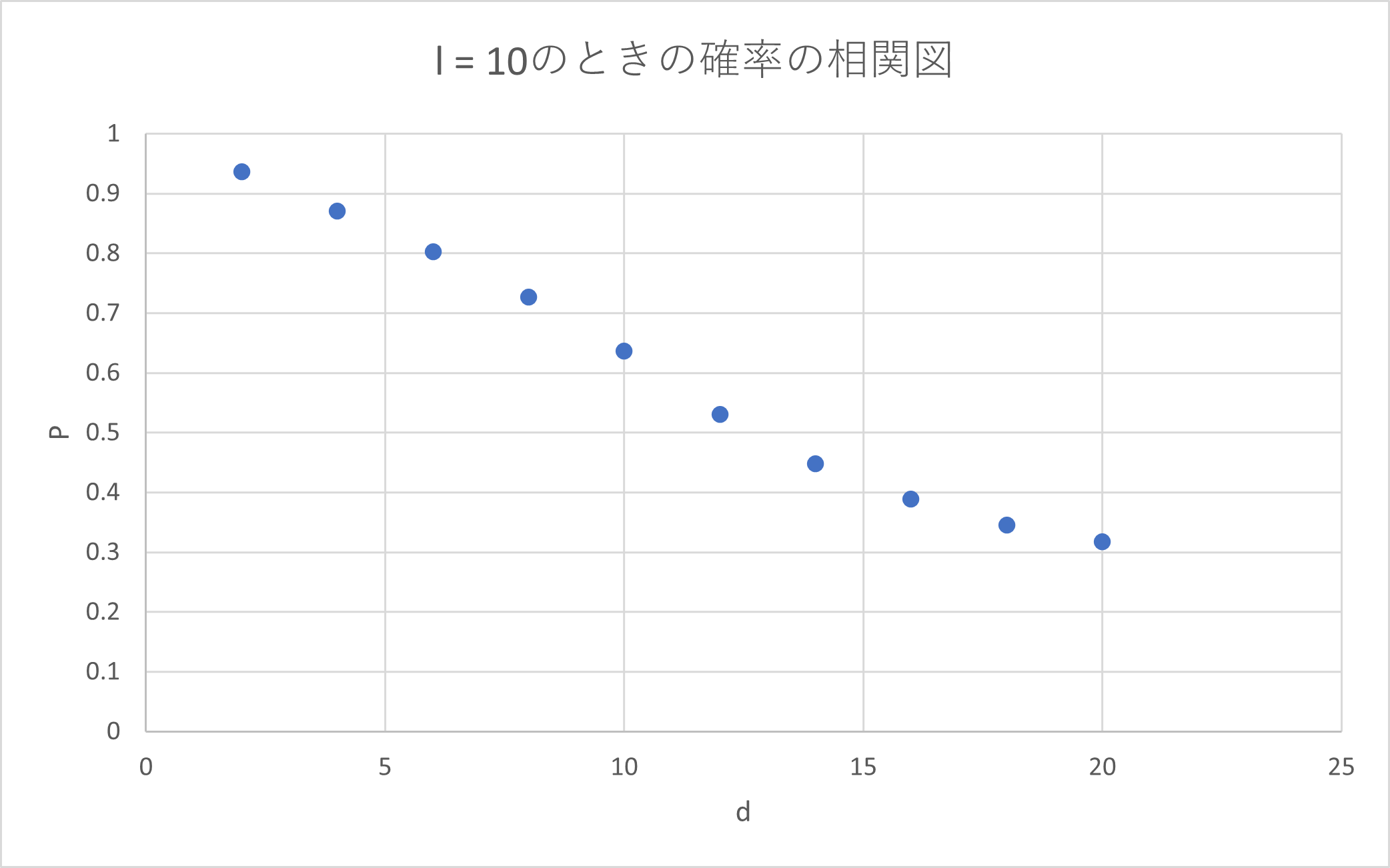
こちらも ![]() の場合と
の場合と ![]() の場合で関係性が違いそうです。
の場合で関係性が違いそうです。
![]() の場合は反比例してるように見えますが図では分かりづらいため、確率の逆数との関係を見てみると、
の場合は反比例してるように見えますが図では分かりづらいため、確率の逆数との関係を見てみると、
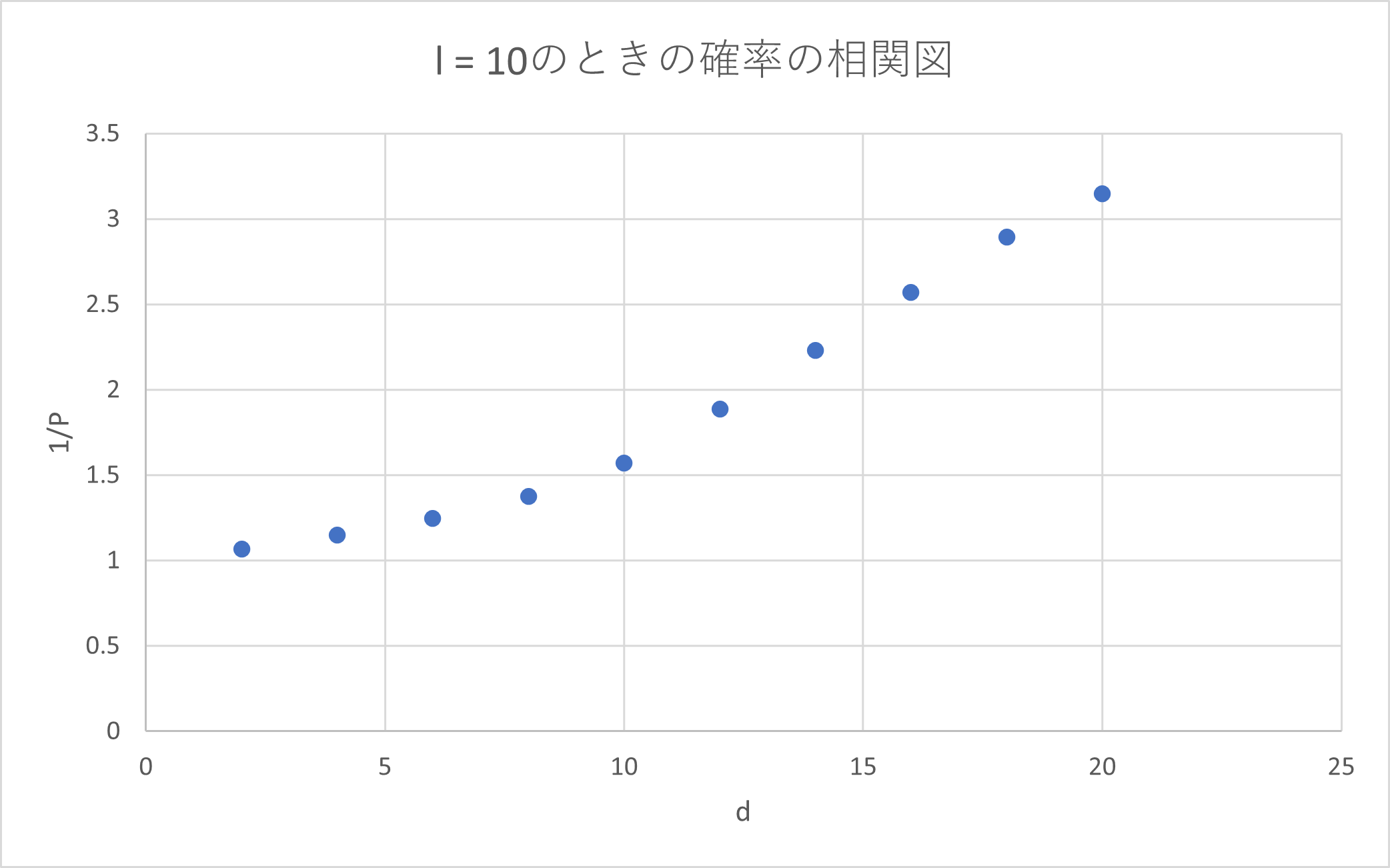
ということで、以下の関係性があると考えられます。
![]()
上記のことをまとめると、 ![]() の場合は以下の関係性となりそうです。
の場合は以下の関係性となりそうです。
![]()
つまり、
![]()
と書くことができます。
揃っているデータを代入すると係数 ![]() が分かります。
が分かります。
| l | d | P | α |
|---|---|---|---|
| 10 | 12 | 0.5303 | 0.6364 |
| 10 | 14 | 0.4484 | 0.6278 |
| 10 | 16 | 0.3891 | 0.6226 |
| 10 | 18 | 0.3455 | 0.6219 |
| 10 | 20 | 0.3178 | 0.6356 |
| 2.5 | 20 | 0.0796 | 0.6368 |
| 5 | 20 | 0.1589 | 0.6356 |
| 7.5 | 20 | 0.2386 | 0.6363 |
| 10 | 20 | 0.3181 | 0.6362 |
| 12.5 | 20 | 0.3980 | 0.6368 |
| 15 | 20 | 0.4772 | 0.6363 |
| 17.5 | 20 | 0.5570 | 0.6366 |
| 20 | 20 | 0.6367 | 0.6367 |
| 2.5 | 30 | 0.0533 | 0.6396 |
| 5 | 30 | 0.1061 | 0.6366 |
| 7.5 | 30 | 0.1591 | 0.6364 |
| 10 | 30 | 0.2123 | 0.6369 |
| 12.5 | 30 | 0.2645 | 0.6348 |
| 15 | 30 | 0.3178 | 0.6356 |
| 17.5 | 30 | 0.3717 | 0.6372 |
| 20 | 30 | 0.4234 | 0.6351 |
| 22.5 | 30 | 0.4762 | 0.6349 |
| 25 | 30 | 0.5306 | 0.6367 |
| 27.5 | 30 | 0.5841 | 0.6372 |
| 30 | 30 | 0.6367 | 0.6367 |
上記データから ![]() の中央値を取ると
の中央値を取ると
![]() です。
です。
結論を総合すると、
![]() の場合、
の場合、
![]()
となります。
今回利用したプログラムは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 |
using System; using System.Collections.Generic; using System.Linq; namespace ConsoleApp3 { class Program { static void Main(string[] args) { var buffon = new Buffon(); // 落とす領域は600×600に固定[ // 試行回数は1,000,000回 var canvasSize = 600; var tryCount = 1000000; //var d = 20; //var c = 2.5; //for (var i = 1; i * c <= d * 2; i++) //{ // ConsoleWrite(buffon.BuffonsNeedle(tryCount, canvasSize, i * c, d)); //} var l = 20; var c = 2; for (var i = 1; i * c <= l * 2; i++) { ConsoleWrite(buffon.BuffonsNeedle(tryCount, canvasSize, l, i * c)); } } /// <summary> /// 出力のフォーマットを揃えるためのメソッド /// </summary> /// <param name="result">n = , l = , d = , count = , P = , 1/P = </param> private static void ConsoleWrite(Result result) { var p = Math.Round(result.GetProbability(), 4, MidpointRounding.AwayFromZero); var revP = Math.Round(1 / result.GetProbability(), 4, MidpointRounding.AwayFromZero); Console.WriteLine($"n = {result.NeedleNum}, l = {result.NeedleLength}, d = {result.Definition}, count = {result.CrossCount}, P = {p}, 1/P = {revP}"); } } public class Buffon { private static readonly Random random = new(); private static double Random(double max, double min) { return random.NextDouble() * (max - min) + min; } public Result BuffonsNeedle(int needleNum, double canvasSize, double needleLen, double defenition) { var lines = new List<Line>(); int lineNum = (int)(canvasSize / defenition); // 平行線を作成する for (var i = 0; i < lineNum; i++) { var y = canvasSize * (i + 0.5) / (double)lineNum; lines.Add(new Line() { Y = y }); } var count = 0; var list = new List<Needle>(); var lineY = lines.Select(x => x.Y).OrderBy(x => x); for (var i = 0; i < needleNum; i++) { var centerX = Random(canvasSize * 0.95, canvasSize * 0.05); var centerY = Random(canvasSize * 0.95, canvasSize * 0.05); // 角度をランダムで決める var theta = Random(2 * Math.PI, 0); var deltaX = needleLen * Math.Cos(theta) / 2; var deltaY = needleLen * Math.Sin(theta) / 2; var item = new Needle() { Coordinate1 = new Coordinate() { X = centerX + deltaX, Y = centerY + deltaY }, Coordinate2 = new Coordinate() { X = centerX - deltaX, Y = centerY - deltaY } }; list.Add(item); var large = item.Coordinate1.Y - item.Coordinate2.Y > 0 ? item.Coordinate1.Y : item.Coordinate2.Y; var small = item.Coordinate1.Y - item.Coordinate2.Y > 0 ? item.Coordinate2.Y : item.Coordinate1.Y; var target = lineY.LastOrDefault(x => x <= large); if (target >= small) { count++; item.IsCross = true; } } return new Result() { CrossCount = count, Needles = list, NeedleNum = needleNum, Definition = defenition, NeedleLength = needleLen }; } } public class Result { public double NeedleLength { get; set; } public double Definition { get; set; } public IList<Needle> Needles { get; set; } public int CrossCount { get; set; } public int NeedleNum { get; set; } public double GetProbability() => this.CrossCount / (double)this.NeedleNum; } public class Needle { public Coordinate Coordinate1 { get; set; } public Coordinate Coordinate2 { get; set; } public bool IsCross { get; set; } = false; } public class Coordinate { public double X { get; set; } public double Y { get; set; } } public class Line { public double Y { get; set; } } } |
考察
確率に  が出現した理由
が出現した理由
今回の確率に ![]() が出てきたことは角度が関係あります。
が出てきたことは角度が関係あります。
理系の方はよく知っていると思いますが、弧度法における角度はラジアンで表されて、 ![]() です。
です。
コードにも記載しておりますが、ランダムで角度を設定する際に上記ラジアンを用いています。
|
1 2 3 4 |
// 角度をランダムで決める var theta = Random(2 * Math.PI, 0); var deltaX = needleLen * Math.Cos(theta) / 2; var deltaY = needleLen * Math.Sin(theta) / 2; |
そのためランダムな角度で針を落下させるということを考えると、確率に ![]() が出てくることも納得ができると思います。
が出てくることも納得ができると思います。
針の長さと平行線の幅の長さによる場合分け
![]() の場合と
の場合と ![]() の場合で振る舞いが変わった理由に関しては凄く単純化して考えてみましょう。
の場合で振る舞いが変わった理由に関しては凄く単純化して考えてみましょう。
![]() の場合
の場合
針の長さがほぼ平行線の幅と同じ時を考えます。
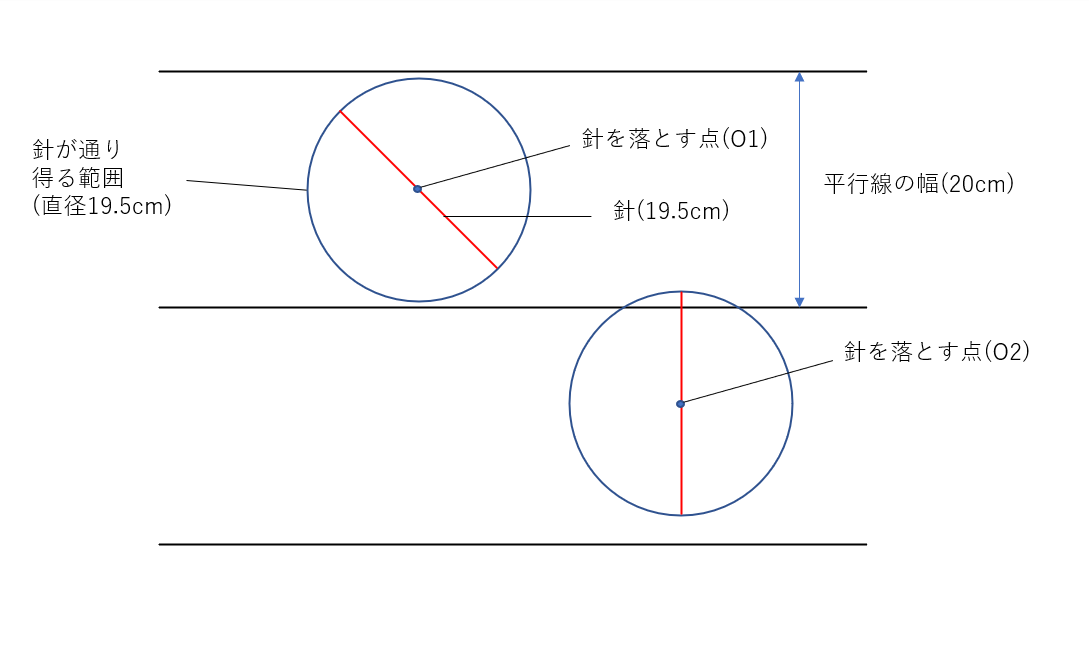
上図にあるように、以下の 2 パターンが存在しています。
- 平行線と平行線のちょうど間の点 O1 に針の中心を落とした場合はどの角度で落としても平行線と交わることは無い。
そのように、どの角度で針を落としても平行線と交わることの無い点が存在する領域を領域 A と呼ぶ - 点 O2 に張りの中心を落とした場合は特定の角度の場合は平行線と交わる。
そのように針を落とした時、特定の角度で平行線と交わる点が存在する領域を領域 B と呼ぶ
![]() の場合
の場合
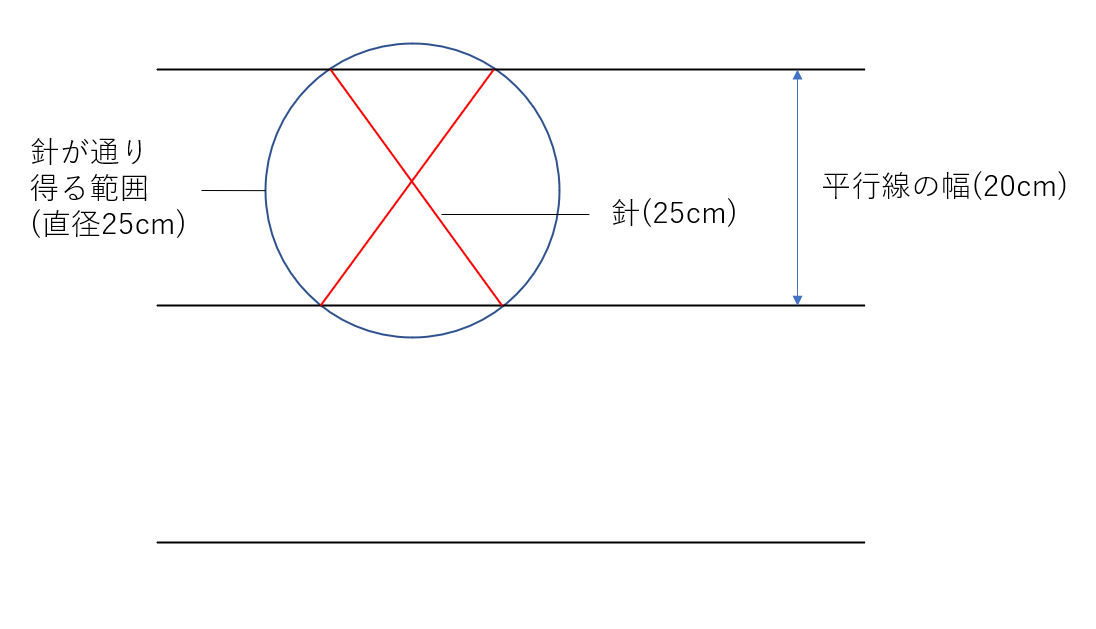
上図にあるように、領域 A が存在せずすべての空間が領域 B となり、性質が異なるために差が生じることになります。
おわりに
今回はモンテカルロシミュレーションで日常ではあまり馴染みの無い値が出る確率に関して紹介しました。
難しい数式をできるだけ省いて、シミュレーションでできる範囲を述べているので、より詳しく知りたい人は調べてみると数学的に面白いことが分かったりするかもしれません。
ではまた次回も見ていただけますと幸いです。
参考図書
直感を裏切る数学 「思い込み」にだまされない数学的思考法
https://www.amazon.co.jp/dp/B00RXCOQDK/

