こんにちはtetsuです。
今回は外れ値検知や異常検知で使われるOne Class Support Vector Machine(よくOCSVMやOne Class SVMと略されます。本稿ではOne Class SVMと略すことにします。)の概要と導出について述べていきたいと思います。ベクトルの演算ができれば、最後のラグランジュの未定乗数法の部分を除いて問題なく読める想定です。
One Class Support Vector Machineとは?
One Class SVMは大多数が正常であるようなデータの集合![]() をもとに学習をおこない、未知のデータが正常であるのか、異常であるのかを判定する手法です。一般には正常に作られた製品や正常な状態のデータは多く手に入れることができても、異常な製品や異常な状態のデータはあまり手に入りません。そのようなケースに対してOne Class SVMを適用することが可能です。
をもとに学習をおこない、未知のデータが正常であるのか、異常であるのかを判定する手法です。一般には正常に作られた製品や正常な状態のデータは多く手に入れることができても、異常な製品や異常な状態のデータはあまり手に入りません。そのようなケースに対してOne Class SVMを適用することが可能です。
One Class Support Vector Machineの導出
早速One Class SVMの導出に入っていきますが、まずはハードマージン最大化というものを紹介し、その後にソフトマージン最大化の場合について述べます。
ハードマージン最大化
One Class SVMでは次のような関数を用いて未知のデータ![]() が正常なのか、異常なのかを判定します。
が正常なのか、異常なのかを判定します。
![]()
ここで![]() はそれぞれ学習によって得るパラメータです。
はそれぞれ学習によって得るパラメータです。
![]() に対する
に対する![]() の値が0より大きいときに
の値が0より大きいときに![]() は正常と判定され、0より小さいときに
は正常と判定され、0より小さいときに![]() は異常と判定されます。
は異常と判定されます。![]() となるような
となるような![]() の集まりによって作られる境界線が正常か異常かの分かれ目になるため、この境界を識別平面といいます。
の集まりによって作られる境界線が正常か異常かの分かれ目になるため、この境界を識別平面といいます。
ここで問題となるのは![]() をどう求めるかになります。
をどう求めるかになります。
One Class SVMでは次のような目標に沿って![]() を求めます。
を求めます。
原点と識別平面との距離が最大になるように
ただし、すべてのデータ
![]()
この目標1を達成している状態を2次元の図であらわすと次のようになります。緑の丸が学習に用いられたデータで、黄色の線が識別平面になります。すべてのデータが黄色の識別平面を境にして原点と反対側(あるいは識別平面上)に位置するように識別平面が決定されています。
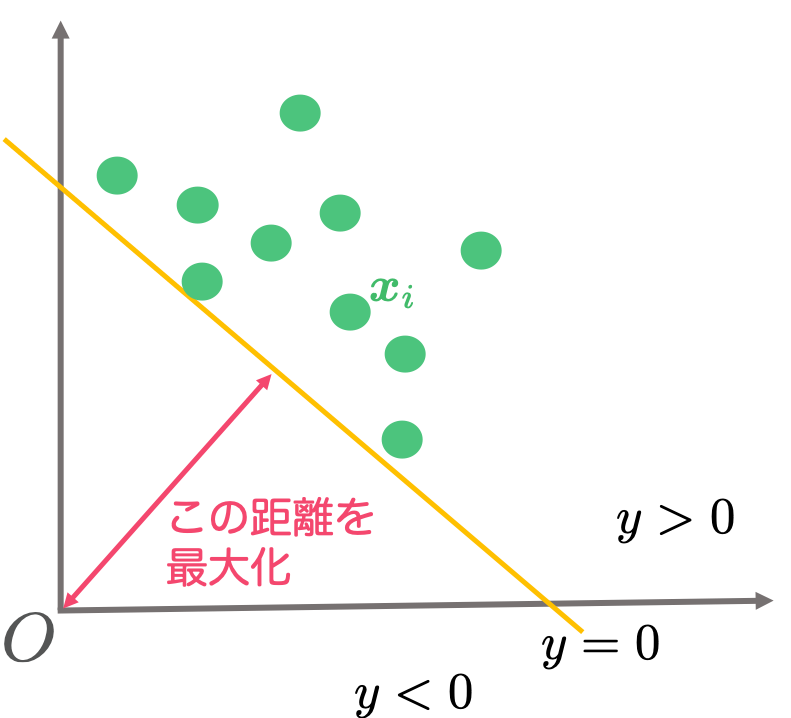
2次元の場合には図にしてみることでそれらしい識別平面が引けますが、実際には![]() がもっと大きい次元のベクトルになるので図にすることができません。次からは数式を使って目標1を達成する方法を考えます。
がもっと大きい次元のベクトルになるので図にすることができません。次からは数式を使って目標1を達成する方法を考えます。
まず先に知っておくと便利な性質を示します。以下のようなものです。
これは識別平面上の異なる適当な2点を![]() とおいたときに、
とおいたときに、
![]()
が成り立つことを利用して示すことができます。1つめの式から2つめの式を引くことで![]() が得られ、
が得られ、![]() と
と![]() が直交することがわかります。
が直交することがわかります。![]() は下の図のように識別平面と平行なベクトルですので、
は下の図のように識別平面と平行なベクトルですので、![]() は識別平面と直交するといえます。
は識別平面と直交するといえます。
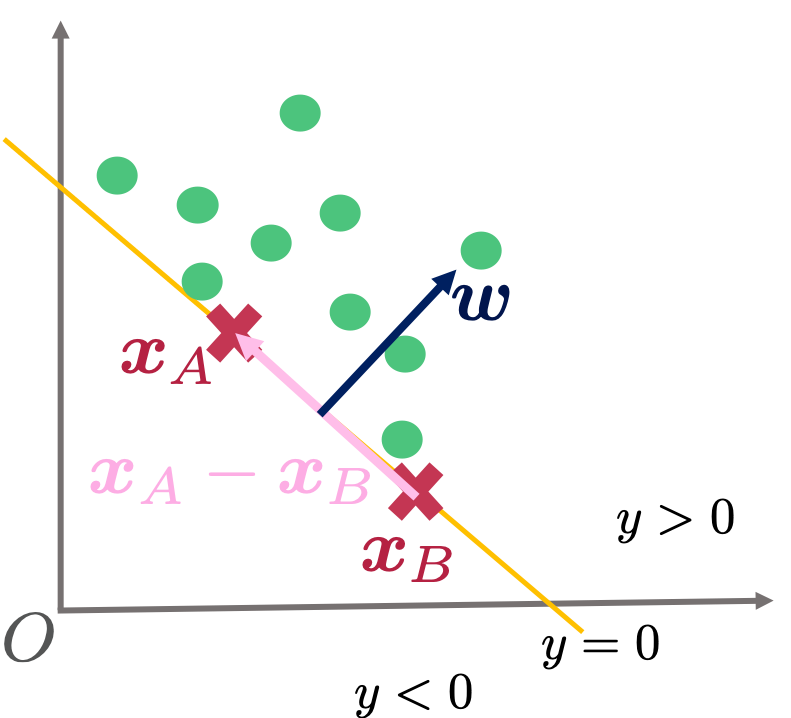
次に原点から識別平面までの距離を数式として求めていきます。
まず長さが![]() で
で![]() と同じ向きであるようなベクトル
と同じ向きであるようなベクトル![]() について考えてみます。変数を色々と定義しますので、次の図を適宜参照下さい。
について考えてみます。変数を色々と定義しますので、次の図を適宜参照下さい。
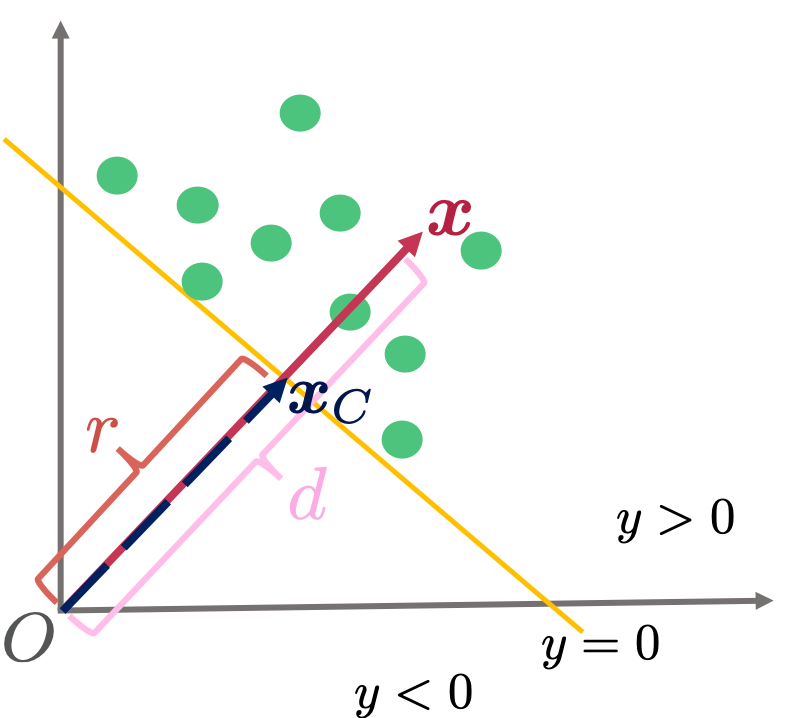
![]() は長さ
は長さ![]() で
で![]() と同じ向きのベクトルであるという定義から以下のようにあらわされます。
と同じ向きのベクトルであるという定義から以下のようにあらわされます。
![]()
ここで![]() はベクトル
はベクトル![]() の長さをあらわします。
の長さをあらわします。
両辺に対して![]() との内積をとれば、
との内積をとれば、
(1) ![]()
という関係を得ることができます。
ここで、この![]() の長さが原点と識別平面までの距離(
の長さが原点と識別平面までの距離(![]() と置いておきます)であるケースを考えてみます。そのようなベクトルを
と置いておきます)であるケースを考えてみます。そのようなベクトルを![]() とおくと、
とおくと、![]() は識別平面の上にありますので、
は識別平面の上にありますので、![]() となります。式(1)にこの関係を当てはめると、次が求まります。
となります。式(1)にこの関係を当てはめると、次が求まります。
![]()
ついでとなりますが、ここで識別平面から任意の![]() までの符号付きの距離を以下のように求めておきます。
までの符号付きの距離を以下のように求めておきます。
(2) ![]()
以上から原点から識別平面までの距離は![]() とわかりましたので、これを最大化したときに目的の
とわかりましたので、これを最大化したときに目的の![]() と
と![]() が求まります。ただし、後々の計算の利便さのために式を少し書き換えます。式をよくみてみると、
が求まります。ただし、後々の計算の利便さのために式を少し書き換えます。式をよくみてみると、![]() を最大化することは
を最大化することは![]() を最小化することと等しいことがわかります。また
を最小化することと等しいことがわかります。また![]() の部分は
の部分は![]() としても最小化問題には影響を及ぼさないため、便宜上このように置きます。
としても最小化問題には影響を及ぼさないため、便宜上このように置きます。
以上のような最大化問題の書き換えの結果、One Class SVMで達成するべき目標1の内容は次のようにあらわされます。
次の最小化問題を解く。
![]()
ただしすべてのデータ![]() に対して、
に対して、
![]()
この問題を(機械的に)解くことで、はじめに示した図にあるような識別平面を求めることができます。
ここまでで労力をかけて式変形などを色々とおこなってきましたが、実は紹介してきた方法には問題があります。次に問題点について述べ、これを解決するソフトマージン最大化のOne Class SVMの説明に移ります。
ハードマージン最大化のOne Class SVMの問題点
はじめにデータの集合![]() は大多数が正常データであると仮定をしました。この仮定にのっとり、例えば2つだけ異常なデータが混ざっているとしたらどうなるかを考えてみます。図示すると次のようなケースです。
は大多数が正常データであると仮定をしました。この仮定にのっとり、例えば2つだけ異常なデータが混ざっているとしたらどうなるかを考えてみます。図示すると次のようなケースです。
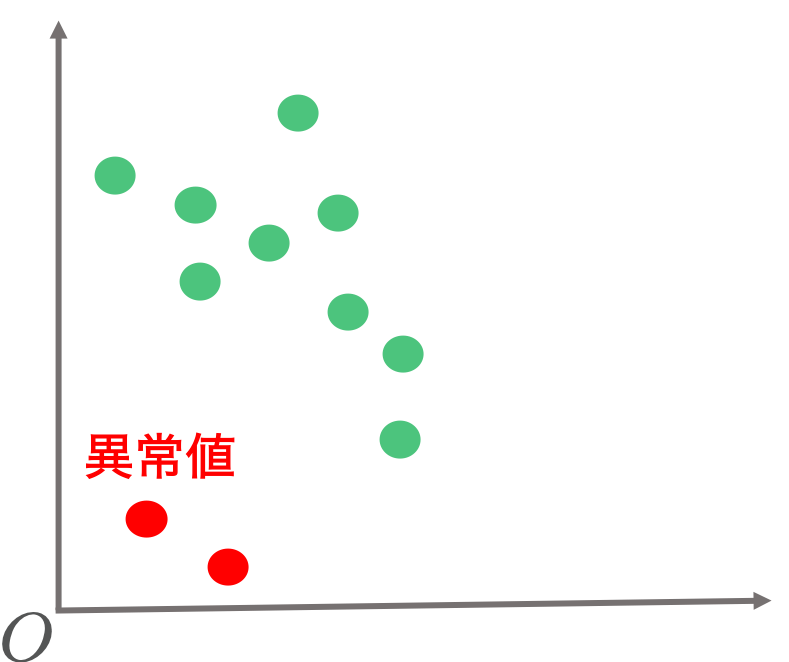
このような状況で目標1の最小化問題を解くと、次のオレンジ色のような識別平面が引かれることになります。
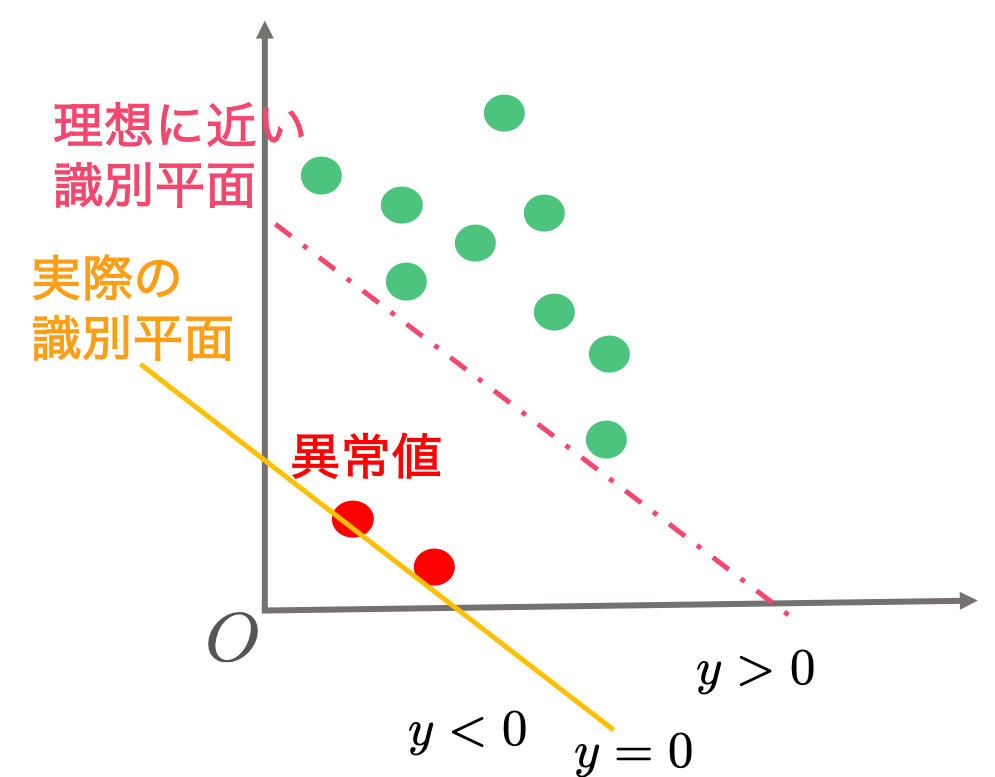
見てわかる通り、オレンジ色の識別平面は異常データの影響を大きく受けて極端に原点に近くなります。実際には異常データであっても、異常と判定されないように識別平面を求めているからです。このようなケースでは異常と判定したいデータの多くが正常と判定されてしまう恐れがあります。理想的にはデータの中に異常データがあったとしても、これらの影響をあまり受けずに赤い点線に近い識別平面を引きたいところです。次に紹介するソフトマージン最大化は異常データの影響を大きく受ける問題を回避することができます。
ソフトマージン最大化
先程まで考えていた目標1では識別平面と原点の間には学習に用いたデータ点が存在しないように識別平面を求めていました。この条件を緩めて、識別平面を求める際に学習に用いたデータが識別平面から原点の間に位置することを許容するようにしてしまいます。これをソフトマージン最大化といいます。一方で識別平面と原点の間にデータが位置しないようにする目標1のことはハードマージン最大化といいます。
ソフトマージン最大化ではそれぞれのデータ![]() は
は![]() の長さだけ識別平面を超えてもよいとします。この
の長さだけ識別平面を超えてもよいとします。この![]() 自身も学習によって求める量であり、なるべく小さくします(=原点側にデータが位置するのを許容するといっても、その量は多くないほうがよい)。
自身も学習によって求める量であり、なるべく小さくします(=原点側にデータが位置するのを許容するといっても、その量は多くないほうがよい)。![]() ができるだけ小さくなるように、目標1の最小化するべき式を次のように書き換えます。
ができるだけ小さくなるように、目標1の最小化するべき式を次のように書き換えます。
(3) 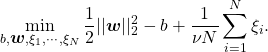
ここで![]() は原点側にデータが超えるのをどの程度許容するのかをあらわす値になり、小さいほど原点側により多くのデータが位置することになります(なぜそう言えるのかは最後に示します)。この値は事前に人が与える必要があります。
は原点側にデータが超えるのをどの程度許容するのかをあらわす値になり、小さいほど原点側により多くのデータが位置することになります(なぜそう言えるのかは最後に示します)。この値は事前に人が与える必要があります。
目標1の条件の部分![]() はどうなるでしょうか。
はどうなるでしょうか。![]() までは識別平面を超えてもよいということから、式(2)の
までは識別平面を超えてもよいということから、式(2)の![]() を
を![]() に置き換えることで(原点側に超えるため、マイナスがついています)
に置き換えることで(原点側に超えるため、マイナスがついています)
(4) 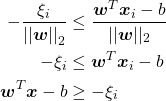
という条件が導かれます。
最小化するべき式(3)と条件(4)から、ソフトマージン最大化でのOne Class SVMで解くべき問題が定まります。
次の最小化問題を解く。
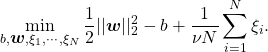
ただしすべてのデータ![]() に対して、
に対して、
![]()
以上でソフトマージン最大化での定式化ができました。この目標2に沿って識別平面を求めていくことで、学習に用いるデータに異常データが含まれていてもその影響を緩和することができます。
実際にはこの最小化問題をこのまま解くのではなく、ラグランジュの未定乗数法を用いて二次計画問題へ落とし込みます。ラグランジュの未定乗数法自身の話と計算の詳細は割愛しますが、計算を進めることで次のような最小化問題が導かれます。
次の最小化問題を解く。
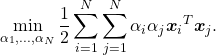
ただし、
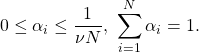
この最小化問題を解いて![]() を求めることで、もともと求めたかったパラメータ
を求めることで、もともと求めたかったパラメータ![]() と
と![]() は
は
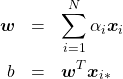
のようにして得られます。ここで![]() を求める際にあらわれる
を求める際にあらわれる![]() は
は
![]()
となるようなデータの番号になります。
![]() でしたので、
でしたので、![]() が成り立ちます。
が成り立ちます。![]() に対応している
に対応している![]() は予測
は予測![]() に全く影響を与えません。一方で
に全く影響を与えません。一方で![]() となる
となる![]() は予測に影響を与え、このような
は予測に影響を与え、このような![]() をサポートベクトルといいます。
をサポートベクトルといいます。
最後に![]() の意味について補足します。ラグランジュの未定乗数法の計算過程からわかりますが、
の意味について補足します。ラグランジュの未定乗数法の計算過程からわかりますが、![]() となるような
となるような![]() に対応する
に対応する![]() は識別平面と原点の間に位置するデータとなります。識別平面と原点の間に位置するデータの数を
は識別平面と原点の間に位置するデータとなります。識別平面と原点の間に位置するデータの数を![]() とおくと、次が導かれます。
とおくと、次が導かれます。
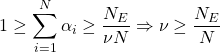
よって![]() は学習に用いたデータの中で識別平面と原点との間に位置するデータの割合の上限となります。このことから、
は学習に用いたデータの中で識別平面と原点との間に位置するデータの割合の上限となります。このことから、![]() を小さくすると識別平面を超えて原点側に位置するデータの数が少なくなるといえます。逆に、大きくすることで原点側に位置するデータの数が多くなるような識別平面ができます。
を小さくすると識別平面を超えて原点側に位置するデータの数が少なくなるといえます。逆に、大きくすることで原点側に位置するデータの数が多くなるような識別平面ができます。
まとめ
今回はOne Class SVMとその導出を紹介しました。One Class SVMはscikit-learnで気軽に試すことが可能ですので、気になった方はぜひ遊んでみて下さい。なお、今回はデータ点![]() をそのまま使用しましたが、一般にはある関数
をそのまま使用しましたが、一般にはある関数![]() で
で![]() を射影した
を射影した![]() を扱います。これにより、データの分布が複雑な問題も解けるようになります。実際に使用する場合にはお気をつけ下さい。
を扱います。これにより、データの分布が複雑な問題も解けるようになります。実際に使用する場合にはお気をつけ下さい。

