はじめに
今回も前回に引き続き、深層学習で使われる要素技術をひとつ紹介する。今回紹介するのは「Label Smoothing」と呼ばれる手法である。
交差エントロピー
いま、![]() 分類の問題を考える。このときの処理を以下に示す。
分類の問題を考える。このときの処理を以下に示す。
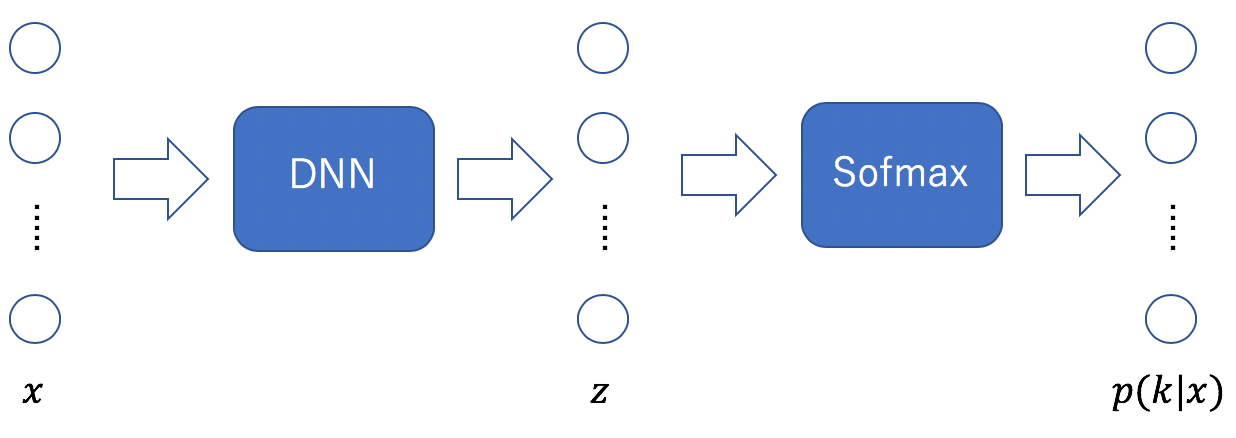
何らかのDNNで処理したあと最終層においてSoftmax関数を適用するのが一般的である。ここでは、入力値を![]() 、Softmax関数への入力値を
、Softmax関数への入力値を![]() とおいた。両者ともベクトルであり、特に
とおいた。両者ともベクトルであり、特に![]() である。Softmax関数の出力値は次式で定義される。
である。Softmax関数の出力値は次式で定義される。
(1) ![]()
この式は入力値![]() がカテゴリ
がカテゴリ![]() に属する確率である。Ground Truthとなる確率を
に属する確率である。Ground Truthとなる確率を![]() とおけば、次の交差エントロピーが損失関数となる。
とおけば、次の交差エントロピーが損失関数となる。
(2) 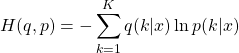
これを最小にするようにDNN内の重みが決定される。![]() に対してはone-hotベクトルが与えられる。
に対してはone-hotベクトルが与えられる。
過学習
![]() を考え、入力値
を考え、入力値![]() に対する正解カテゴリが
に対する正解カテゴリが![]() であるとする。このとき
であるとする。このとき![]() と書くことができる。交差エントロピーを最小にするように学習を行うと、
と書くことができる。交差エントロピーを最小にするように学習を行うと、![]() は1に、
は1に、![]() は0に近づいていくことになる。すなわち
は0に近づいていくことになる。すなわち
(3) ![]()
が1に近づくとき、![]() は大きく、
は大きく、![]() は小さくなる。
は小さくなる。![]() と
と![]() の間の距離が大ければ大きいほど、
の間の距離が大ければ大きいほど、![]() に近づいていく(参考のため指数関数の変化の様子を以下に示す)。
に近づいていく(参考のため指数関数の変化の様子を以下に示す)。
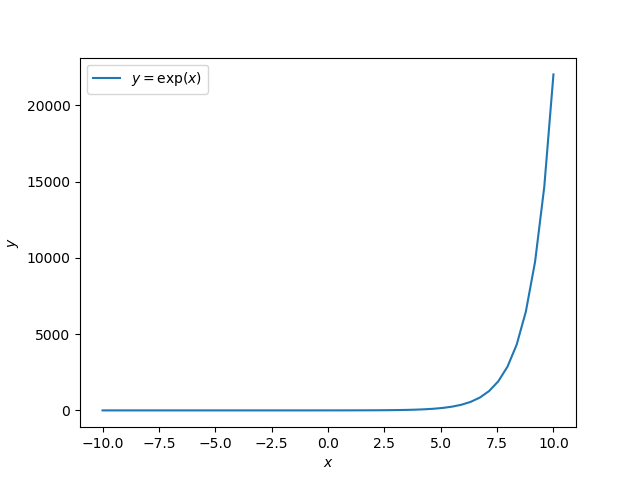
しかし、![]() と
と![]() の間の距離を極端に大きくすると過学習となり、汎化能力を抑制してしまうことがある。
の間の距離を極端に大きくすると過学習となり、汎化能力を抑制してしまうことがある。
Label Smoothing
過学習を抑えるメカニズムはこれまで種々提案されているが、Label Smoothingもその中のひとつである。入力値![]() がカテゴリ
がカテゴリ![]() に属する時、先に与えた
に属する時、先に与えた![]() は次式で表現できる。
は次式で表現できる。
(4) ![]()
ここで、![]() は、
は、![]() のとき1、
のとき1、![]() のとき0となる関数である。この「極端」な値の割り当てを緩和し、過学習を抑えようというアイデアがLabel Smoothingである。すなわち、次式を考える。
のとき0となる関数である。この「極端」な値の割り当てを緩和し、過学習を抑えようというアイデアがLabel Smoothingである。すなわち、次式を考える。
(5) ![]()
ここで、![]() は全ての
は全ての![]() について何らかの値を持つ関数である。重み
について何らかの値を持つ関数である。重み![]() でこの関数を追加することにより、
でこの関数を追加することにより、![]() のときにも
のときにも![]() は値を持つことができる。
は値を持つことができる。![]() として、一様分布が使われることが多い。
として、一様分布が使われることが多い。
(6) ![]()
以下の簡単なコードで、重み![]() が損失関数にもたらす効果を
が損失関数にもたらす効果を![]() の場合に見てみる。
の場合に見てみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt # 擬似的に予測値を作成する。 def make_prediction(x, dim): d = x + dim - 1 a = np.array([1 / d] * dim) a[1] = x / d return a # 1番目だけ1の正解値。 def make_ground_truth(dim): a = np.zeros(dim) a[1] = 1 return a # Label Smoothingを考慮した正解値。 def make_ground_truth_with_label_smoothing(dim, epsilon): a = make_ground_truth(dim) b = np.ones(dim) * (1 / dim) return (1 - epsilon) * a + epsilon * b # 交差エントロピーを計算する。 def calculate_cross_entropy(ps, gs): return -np.sum(np.log(ps) * gs) if __name__ == "__main__": # 正解値 step = 0.05 gts = [make_ground_truth_with_label_smoothing(dim=5, epsilon=step * i) for i in range(5)] losses = [] n = 100 for gt in gts: tmp = [] for x in range(1, n): ps = make_prediction(x=x, dim=5) loss = calculate_cross_entropy(ps, gt) tmp.append(loss) losses.append(tmp) plt.grid() for i, loss in enumerate(losses): plt.plot(np.arange(1, n), loss, label='epsilon={:.2f}'.format(i * step)) plt.xlabel('x') plt.ylabel('Loss') plt.legend(loc='best') plt.savefig('./result.png') |
- 9-13行目:
xを与えると擬似的な予測値ベクトルを生成する関数である。dim=5としたので5次元ベクトルである。xが大きくなると正解値[0,1,0,0,0]に近づいていく。 - 24-27行目:Label Smoothingを考慮した
 を作成する関数である。
を作成する関数である。dim=5。epsilonは に相当する。
に相当する。 - 31-32行目:損失(交差エントロピー)を計算する。
このコードを実行すると、次の図を得る。横軸xの値が大きくなると擬似的な予測値が[0,1,0,0,0]に近づいていくことに注意する。
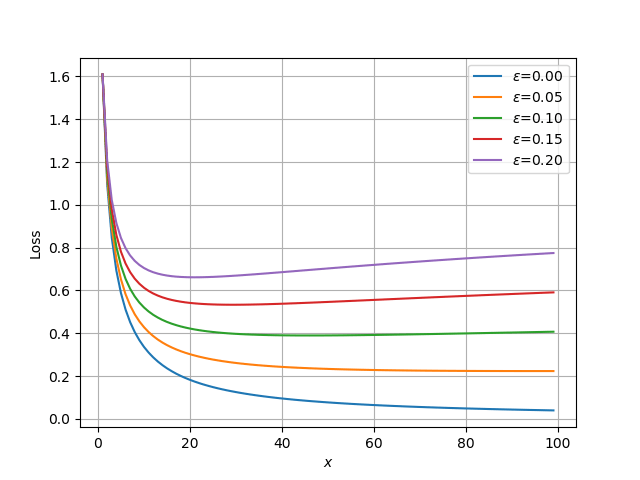
![]() が0のときはLabel Smoothingの効果はないので、通常の学習に見られる減衰曲線となる。
が0のときはLabel Smoothingの効果はないので、通常の学習に見られる減衰曲線となる。![]() の値を増やしていくと損失の減衰が抑制され、途中から増大に転ずる様子を見ることができる。増加に転じる近傍で学習を止めることで、極端な最適化を抑えることができる。
の値を増やしていくと損失の減衰が抑制され、途中から増大に転ずる様子を見ることができる。増加に転じる近傍で学習を止めることで、極端な最適化を抑えることができる。
まとめ
今回は、過学習を抑制するメカニズムのひとつであるLabel Smoothingを紹介した。Label Smoothing自体はとても簡単なロジックである。参考にした論文では、Label Smoothingにより、ILSVRC 2012のtop-1 errorとtop-5 errorの両方において、0.2%ほどの精度向上が見られたと報告されている。

