はじめに
今回は、ガウス過程のためのPythonライブラリ「GPyTorch」を紹介したい。このページに簡単なチュートリアルがある。このチュートリアルを詳細な理論式で補いながら説明したい。ガウス過程自体の説明は本ブログ(こことここ)でもしているので、興味があれば参照して欲しい。
観測値の作成
(1) 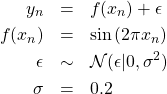
![]() は平均0、分散
は平均0、分散![]() の正規分布を表す。これを実装したのが以下である。
の正規分布を表す。これを実装したのが以下である。
|
1 2 3 4 |
# Training data is 100 points in [0,1] inclusive regularly spaced train_x = torch.linspace(0, 1, 100) # True function is sin(2*pi*x) with Gaussian noise train_y = torch.sin(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * 0.2 |
ガウス過程の導入
いま、![]() 、
、![]() とおき、ベクトル
とおき、ベクトル![]() が次のガウス過程で作られると仮定する。
が次のガウス過程で作られると仮定する。
(2) ![]()
ここで、![]() 、
、![]() である。
である。![]() は平均ベクトル、
は平均ベクトル、![]() は共分散行列である。
は共分散行列である。![]() の成分
の成分![]() として、次のRBFカーネルを仮定する。
として、次のRBFカーネルを仮定する。
(3) 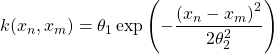
これらを実装したのが次のコードである。
|
1 2 3 4 5 6 7 8 9 10 11 |
# We will use the simplest form of GP model, exact inference class ExactGPModel(gpytorch.models.ExactGP): def __init__(self, train_x, train_y, likelihood): super(ExactGPModel, self).__init__(train_x, train_y, likelihood) self.mean_module = gpytorch.means.ConstantMean() self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel()) def forward(self, x): mean_x = self.mean_module(x) covar_x = self.covar_module(x) return gpytorch.distributions.MultivariateNormal(mean_x, covar_x) |
ExactGPModelは式(2)の正規分布を表すクラスである。コンストラクタ内で、平均ベクトルmean_moduleと共分散行列covar_moduleを定義している。ここでは平均ベクトルとして定数値を仮定する(![]() )。クラス
)。クラスRBFKernelは式(3)の指数関数部分を表す。![]() は、このクラスが持つ変数
は、このクラスが持つ変数lengthscaleに相当する。式(3)のパラメータ![]() は関数
は関数ScaleKernel(6行目)により付与される。関数forwardが返す値は、クラスMultivariateNormalのインスタンスである。
尤度の導入
![]() が式(2)から生成されるとき、
が式(2)から生成されるとき、![]() を生成する分布(尤度)は次式から計算される。
を生成する分布(尤度)は次式から計算される。
(4) 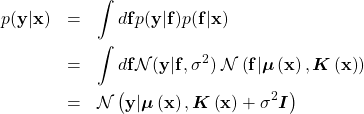
![]() として、
として、![]() とおき、パラメータ依存性を明示的に書くと、
とおき、パラメータ依存性を明示的に書くと、![]() は
は![]() と書くことができる。
と書くことができる。![]() は以下の
は以下のGaussianLikelihoodで定義される。
|
1 2 3 |
# initialize likelihood and model likelihood = gpytorch.likelihoods.GaussianLikelihood() model = ExactGPModel(train_x, train_y, likelihood) |
ExactGPModelを使う場合、その引数likelihoodはGaussianLikelihoodでなければならない。
最適化
(5) ![]()
を最大にするような![]() を勾配降下法により求める。これを実現するコードが以下である。
を勾配降下法により求める。これを実現するコードが以下である。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# this is for running the notebook in our testing framework import os smoke_test = ('CI' in os.environ) training_iter = 2 if smoke_test else 50 # Find optimal model hyperparameters model.train() likelihood.train() # Use the adam optimizer optimizer = torch.optim.Adam([ {'params': model.parameters()}, # Includes GaussianLikelihood parameters ], lr=0.1) # "Loss" for GPs - the marginal log likelihood mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model) for i in range(training_iter): # Zero gradients from previous iteration optimizer.zero_grad() # Output from model output = model(train_x) # Calc loss and backprop gradients loss = -mll(output, train_y) loss.backward() print('Iter %d/%d - Loss: %.3f lengthscale: %.3f noise: %.3f' % ( i + 1, training_iter, loss.item(), model.covar_module.base_kernel.lengthscale.item(), model.likelihood.noise.item() )) optimizer.step() |
7,8行目でmodelとlikelihoodをそれぞれ訓練モードに設定している。PyTorchでお馴染みの手順である。11行目で最適化器Adamを定義する。16行目にあるExactMarginalLogLikelihoodは式(5)に相当する。24行目のlossは
(6) ![]()
の値である。これを最小にするような計算が行われている。ループの中身は、PyTorchを用いたニューラルネットワークの最適化手順と同じである。PyTorchのクラスAdamが使われていることに注意する。上記コードを実行すると以下の出力を得る。
Iter 1/50 – Loss: 0.947 lengthscale: 0.693 noise: 0.693
Iter 2/50 – Loss: 0.916 lengthscale: 0.644 noise: 0.644
Iter 3/50 – Loss: 0.882 lengthscale: 0.598 noise: 0.598
Iter 4/50 – Loss: 0.844 lengthscale: 0.555 noise: 0.554
Iter 5/50 – Loss: 0.801 lengthscale: 0.514 noise: 0.513
Iter 6/50 – Loss: 0.752 lengthscale: 0.476 noise: 0.474
Iter 7/50 – Loss: 0.699 lengthscale: 0.439 noise: 0.437
…
Iter 47/50 – Loss: -0.064 lengthscale: 0.287 noise: 0.029
Iter 48/50 – Loss: -0.066 lengthscale: 0.284 noise: 0.030
Iter 49/50 – Loss: -0.069 lengthscale: 0.282 noise: 0.030
Iter 50/50 – Loss: -0.071 lengthscale: 0.281 noise: 0.031
損失(Loss)とlengthscale(![]() )、noise(
)、noise(![]() )が最適値へ向かう様子が出力される。
)が最適値へ向かう様子が出力される。
予測
予測したい![]() 個の位置を
個の位置を![]() とおく。対応する
とおく。対応する![]() の値
の値![]() は次式で与えられる。
は次式で与えられる。
(7) ![]()
ここで、![]() を改めて
を改めて![]() と置いてある。行列
と置いてある。行列![]() と
と![]() の成分は次式で定義される。
の成分は次式で定義される。
(8) ![]()
行列![]() は対角行列である。これらを計算するのが次のコードである。
は対角行列である。これらを計算するのが次のコードである。
|
1 2 3 4 5 6 7 8 9 |
# Get into evaluation (predictive posterior) mode model.eval() likelihood.eval() # Test points are regularly spaced along [0,1] # Make predictions by feeding model through likelihood with torch.no_grad(), gpytorch.settings.fast_pred_var(): test_x = torch.linspace(0, 1, 51) observed_pred = likelihood(model(test_x)) |
2行目、3行目で評価モードに切り替えている。9行目で式(7)を計算している(MultivariateNormalのインスタンスが作られる)。次のコードでグラフを描く。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
plt.rcParams["font.size"] = 18 plt.figure(figsize=(15,10)) with torch.no_grad(): # Get upper and lower confidence bounds lower, upper = observed_pred.confidence_region() # Plot training data as black stars plt.plot(train_x.numpy(), train_y.numpy(), 'k*') # Plot predictive means as blue line plt.plot(test_x.numpy(), observed_pred.mean.numpy(), 'b') # Shade between the lower and upper confidence bounds plt.fill_between(test_x.numpy(), lower.numpy(), upper.numpy(), alpha=0.5) plt.ylim([-3, 3]) plt.legend(['Observed Data', 'Mean', 'Confidence']) plt.show() |
これを実行すると次の画像を得る。
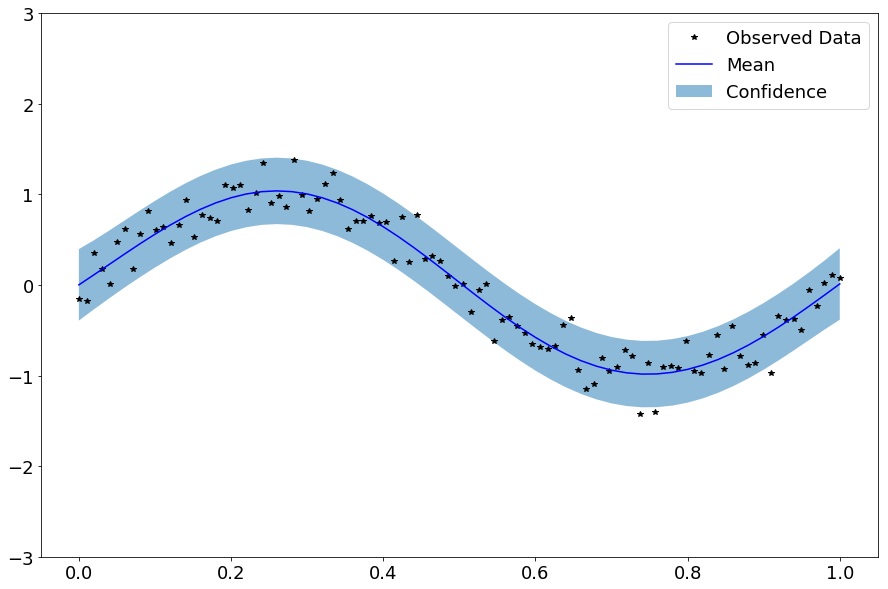
黒の星印は観測値(訓練データ)を、青の曲線は式(7)の平均ベクトル![]() を、淡い青の領域は標準偏差の下限と上限を表す。
を、淡い青の領域は標準偏差の下限と上限を表す。
まとめ
今回は、ガウス過程のためのPythonライブラリ「GPyTorch」のチュートリアルを詳細な理論式で補いながら説明した。深層学習で使われるPyTorchと統一的なコーディングができることが大きなメリットである。
参考文献
- ガウス過程と機械学習:とても良い本である。ベイズ推定による機械学習もおすすめ。

