はじめに
今回は、深層学習を用いたMetric Learningを紹介する。
Metric Learningとは
いま、教師ありの識別問題を考える。観測値![]() と、それぞれの
と、それぞれの![]() に対するラベル
に対するラベル![]() が与えられている。この問題は、特徴空間における境界面(超平面)を求める問題に帰着する。ラベル数が3、特徴ベクトルの次元が2の場合の識別後のイメージ図を、(1)と(2)に示した。
が与えられている。この問題は、特徴空間における境界面(超平面)を求める問題に帰着する。ラベル数が3、特徴ベクトルの次元が2の場合の識別後のイメージ図を、(1)と(2)に示した。
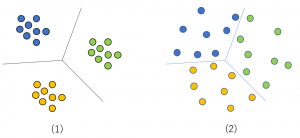
この特徴ベクトルを使い、類似検索を行うことを考える。類似検索では2点間の距離が近いものを選ぶ。従って、図(2)の場合、境界面近傍の点をクエーリにすると、境界をまたがった点(ラベルの異なる点)を選ぶ頻度が高くなる。これを防ぐには、図(1)のように、異なるラベルを持つものは離れ、同じラベルを持つものは密集するようにすれば良い。これを実現する学習法を、Metric Learningと呼ぶ(ここで言うMetricとは距離のことである)。
 -constrained Softmax Loss
-constrained Softmax Loss
Metric Learningを深層学習を用いて行う手法の1つに、「![]() -constrained Softmax Loss」と呼ばれる損失関数を用いる方法がある。これは2017年に提案された手法である(原論文)。この手法の特長は、既存のネットワークの最終層のひとつ前に、たった2層を追加するだけでMetric Learningを行える手軽さである。2017年当時は精度においても他手法より良い結果が得られていた。この原論文の概要を次に説明する。
-constrained Softmax Loss」と呼ばれる損失関数を用いる方法がある。これは2017年に提案された手法である(原論文)。この手法の特長は、既存のネットワークの最終層のひとつ前に、たった2層を追加するだけでMetric Learningを行える手軽さである。2017年当時は精度においても他手法より良い結果が得られていた。この原論文の概要を次に説明する。
原論文では顔認証(face verification)の文脈において本手法を検討している。著者らはまず初めに、特徴ベクトルの長さ(原点からの距離)と顔画像の関係を調べた(下図参照)。
L2-constrained Softmax Loss for Discriminative Face Verificationより
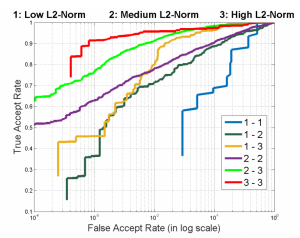
上図の一番上の行の顔は特徴ベクトルの長さが長いもの、一番下の行の顔は特徴ベクトルの長さが短いものである。真ん中の行はどちらでもない長さを持つ特徴ベクトルに相当する画像である。これら3つのカテゴリ間で顔認証(類似検索)を行った結果が下図である。
L2-constrained Softmax Loss for Discriminative Face Verificationより
上図に示されているのはROC曲線と呼ばれる精度指標であり、左上に上がっている曲線ほど精度が良いことを表す。今の場合、赤い曲線(3-3)が一番精度が良い。この曲線は、特徴ベクトルの長さが長い者同士で比較した結果である。一方、一番精度が悪いのが青い曲線(1-1)である。これは特徴ベクトルの長さが短い者同士の比較結果である。以上の結果から、特徴ベクトルの長さが顔認証の精度を大きく左右していることが分かる。そこで著者らは特徴ベクトルの長さをすべて同じにし、最も精度が良くなる長さに揃えるロジックを提案した。彼らが用いたネットワークの構造を以下に示す。
L2-constrained Softmax Loss for Discriminative Face Verificationより
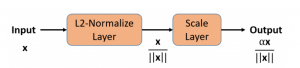
右側に見える橙色の2層を用いて特徴ベクトルの長さを固定値にしている。この2層以外の構造は、Face-Resnetと呼ばれる既存のネットワークである。この2層で処理されるデータの様子を下図に示す。
L2-constrained Softmax Loss for Discriminative Face Verificationより
最初の層で長さを1にし、次の層で長さを固定値![]() に変更している。つまり、半径
に変更している。つまり、半径![]() の超球面上で類似度を見るということである。いくつかの実験により、
の超球面上で類似度を見るということである。いくつかの実験により、![]() が選ばれている。原論文ではいくつかのデータセットに対し本手法を適用した結果が掲載されているが、ここでは省略する。
が選ばれている。原論文ではいくつかのデータセットに対し本手法を適用した結果が掲載されているが、ここでは省略する。
実践
この手法を小さなデータセットMNIST(手書き文字画像)に適用し、その効果を確認する。ベースにするネットワークは、Pytorchのexamples/mnist/main.pyに実装されているものである。このネットワークに上記の2層を追加した(コードをここに置いた)。識別問題として訓練したあと、最終層のひとつ前の層から特徴ベクトルを取り出す。この特徴ベクトルをt-SNEで2次元に圧縮したあとの点の分布を次に示す。
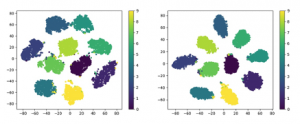
左図は2層を追加しない場合の分布、右図は2層を追加した場合の分布である。MNISTは0から9までの数字を持つので、10個のクラスタが出来上がる。左右の図を比べた時、右の方が各クラスタがギュッと集まっていることが分かる。一番上に示したイメージ図の(2)が左図に、(1)が右図に相当する。同じラベルを持つ点を密集せることで、類似検索を行った際の精度を上げることができる。
まとめ
とても簡単な手続きでMetric Learningを実現できる手法を紹介した。この手法のポイントは、特徴ベクトルの長さを揃えることであり、結果的に2つのベクトルのなす角度だけで類似度を決めていることになる。実際にMNISTに適用しその効果を確認した。