はじめに
以前、この技術ブログで時系列解析を4回に分けて解説した。1回目はMA過程を、2回目はAR過程を、3回目はARMA過程・ARIMA過程・SARIMA過程を取り上げ、4回目で実際のデータにSARIMA過程を適用した結果を示した。最近購入した書籍「Pythonによる時系列予測」に、時系列解析時の大変分かりやすい手順がまとめられていた。今回は、この本に記載された手順に従って、時系列データ解析を行ってみる。使用するプログラミング言語はPythonである。
手順
手順は下図の通りである。テキスト通りでなく、より扱いやすくするために少し変更した。
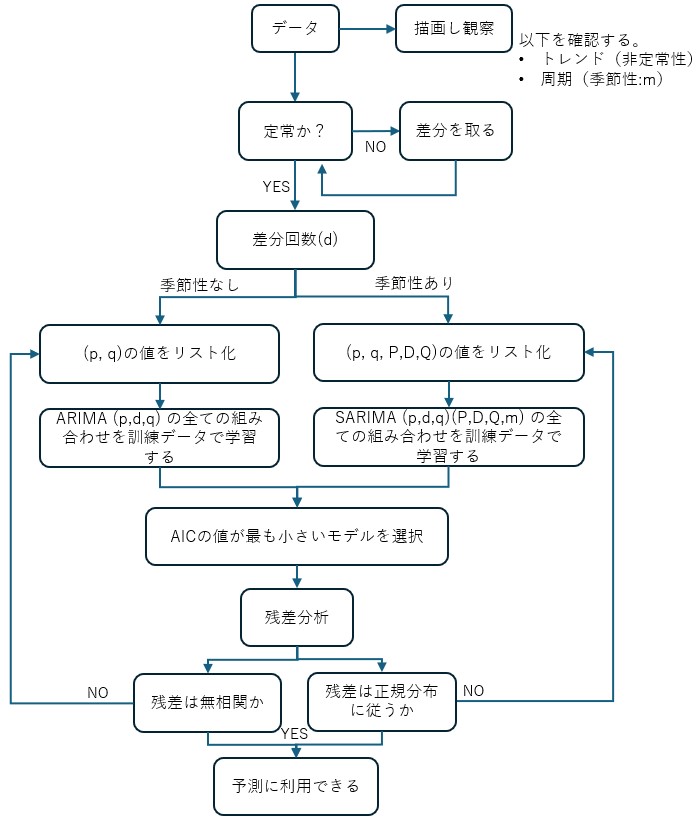
まず最初に、データを描画し、その変化を目視で確認する。時間軸に沿ってマクロな変化(単調増加や単調減少など)が見られる場合、トレンドがあることになり、そのデータは非定常過程である(定常・非定常の定義は過去の記事にまとめてある)。さらに短い期間で周期的な変動がある場合、そのデータには季節性があることになる(季節性に関しては過去の記事にまとめてある)。その周期を![]() とする。
とする。
非定常過程の場合、定常過程に変換する必要がある(その理由は過去の記事にまとめてある)。定常過程への変換を行うには隣接するデータ間の差分を取れば良い。定常過程になるまで差分を繰り返す回数を![]() とする。
とする。
そのあとは、先に見た季節性の有無から利用するモデルを決める。季節性があればSARIMAモデルを、なければARIMAモデルを使う。それぞれのモデルで最適なパラメータを決めるため、赤池情報量基準(AIC)を使う(AICについては過去の記事で説明している)。
最適なパラメータが決定されたあと、残差分析を行う。残差が無相関かつ正規分布に従うならば、そのモデルを予測に使うことができる。ここで残差とは、モデルが予測する値と観測値の差のことである。残差が無相関かつ正規分布に従う場合、採用したモデルの枠内で観測値の再現が十分になされていることを意味する。
使用するデータセット
ここでは、気象庁が提供する二酸化炭素濃度の時系列データを使用する。これにSARIMAを適用し濃度変化を予測する。
ソースコード
今回のソースコードはここにあります。
データの描画
最初にデータの全体図を示す。
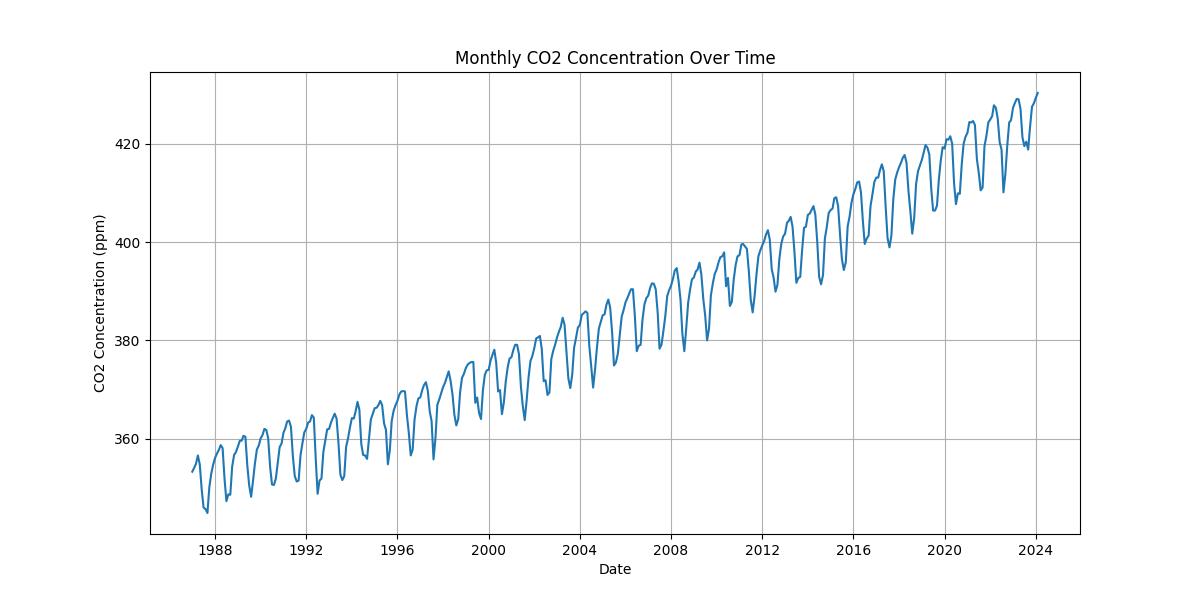
1987年1月から2024年2月までのデータである。縦軸は月平均の二酸化炭素濃度(単位はppm)、横軸は時間軸である。1年は12個のデータから構成される。これを眺めると、単調増加するマクロな変化があることから、この時系列データは非定常過程であることが分かる。また、1年周期のミクロな振動も確認できるので周期性(![]() )を持つことも分かる。
)を持つことも分かる。
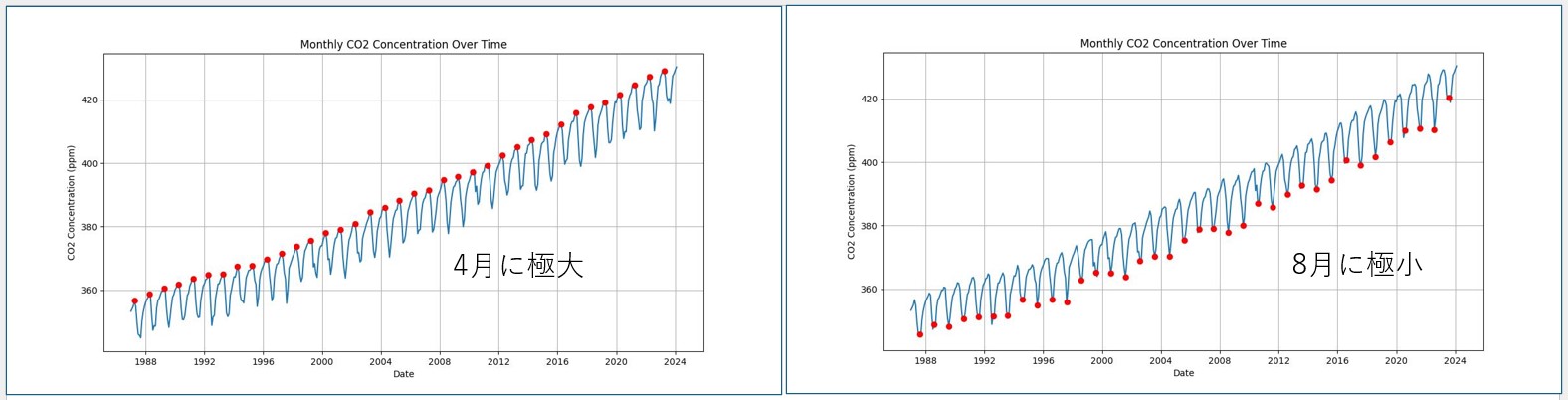
さらに、上の図から4月に極大値(赤丸)、8月に極小値(赤丸)があることが分かる。これは、春から夏にかけて植物の光合成が活発になるため二酸化炭素濃度が急激に落ちることを示している。これが季節的な周期の原因である。
差分回数の決定
上で見たように対象とするデータは非定常過程であるから差分を取ることにより定常過程に変換する必要がある。まず最初に差分を取る前の元データの定常性を判定してみる。その判定には拡張ディッキー・フラー(ADF)検定を用いる。この検定の帰無仮説と対立仮説は以下の通りである。
差分を取る前のデータが非定常であり、差分を取った後のデータが定常であるとき、差分前のデータには単位根があると言う。帰無仮説を棄却できるか否かは、ADF統計量とp値から判定できる。Pythonライブラリstatsmodelsがこの検定をサポートしている。
|
1 2 3 4 5 6 7 8 9 |
from statsmodels.tsa.stattools import adfuller ad_fuller_result = adfuller(data['co2']) criticals = ad_fuller_result[4] print(f'ADF Statistic: {ad_fuller_result[0]}') print(f'p-value: {ad_fuller_result[1]}') print(f"critical 1%: {criticals['1%']}") print(f"critical 5%: {criticals['5%']}") print(f"critical 10%: {criticals['10%']}") |
3行目のdataはデータを格納したDataFrameのインスタンスである。adfullerがADF検定を実行する関数である。これを実行すると以下を得る。
|
1 2 3 4 5 |
ADF Statistic: 2.3490677243905096 p-value: 0.9989842880293069 critical 1%: -3.445613745346461 critical 5%: -2.868269325317112 critical 10%: -2.5703544951308404 |
1行目がADF統計量であり、2行目がp値である。3行目以降は臨界値と呼ばれるものである。
有意水準とは帰無仮説を棄却する基準となる確率のことである。多くの場合0.05(5%)が使われる。計算結果を見ると、帰無仮説は棄却できないことが分かる。つまり、元データは非定常過程であることが分かる。次に1階差分のADF検定を行う。
|
1 2 3 4 5 6 7 8 9 10 |
df_diff = np.diff(data['co2'], n=1) ad_fuller_result = adfuller(df_diff) criticals = ad_fuller_result[4] print(f'ADF Statistic: {ad_fuller_result[0]}') print(f'p-value: {ad_fuller_result[1]}') print(f"critical 1%: {criticals['1%']}") print(f"critical 5%: {criticals['5%']}") print(f"critical 10%: {criticals['10%']}") |
1行目で1階差分を取っている。3行目以降でADF検定を行っている。結果は以下の通り。
|
1 2 3 4 5 |
ADF Statistic: -7.044837391957347 p-value: 5.722230484233865e-10 critical 1%: -3.445613745346461 critical 5%: -2.868269325317112 critical 10%: -2.5703544951308404 |
ADF統計量はどの臨界値よりも小さく、p値は0.05より小さいので、帰無仮説を棄却できる。すなわち1階差分データは定常過程であることが分かる。すなわち、![]() である。
である。
予測モデルのパラメータの最適化
先に見たように元データには季節性がある(![]() )。従って、SARIMAモデルを採用しパラメータ
)。従って、SARIMAモデルを採用しパラメータ![]() の最適化を行う。
の最適化を行う。
|
1 2 3 4 5 6 7 8 9 |
from itertools import product ps = range(0, 4, 1) qs = range(0, 4, 1) Ps = range(0, 4, 1) Qs = range(0, 4, 1) d = 1 D = 1 m = 12 SARIMA_order_list = list(product(ps, qs, Ps, Qs)) |
ここでは、Dについてはあらかじめ1を与えておいた。多くの場合、季節性がある場合はD=1としておけば十分である。d=1,m=12は先に決めたパラメータである。これら以外のパラメータについては0,1,2,3の4つを候補にした。以下のコードで訓練データとテストデータに分割する。テストデータは一番最近の2年分のデータである。
|
1 2 3 |
OFFSET = 24 train = data['co2'][:-OFFSET] test = data.iloc[-OFFSET:] |
以下のコードで最適なパラメータを決める。
|
1 2 |
SARIMA_result_df = optimize_SARIMA(train, SARIMA_order_list, d, D, m) SARIMA_result_df |
ここで、optimize_SARIMAは次の関数である。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
from typing import Union from statsmodels.tsa.statespace.sarimax import SARIMAX def optimize_SARIMA(endog: Union[pd.Series, list], order_list: list, d: int, D: int, s: int) -> pd.DataFrame: results = [] for order in order_list: try: model = SARIMAX( endog, order=(order[0], d, order[1]), seasonal_order=(order[2], D, order[3], s), simple_differencing=False).fit(disp=False) except: continue aic = model.aic results.append([order, aic]) result_df = pd.DataFrame(results) result_df.columns = ['(p,q,P,Q)', 'AIC'] #Sort in ascending order, lower AIC is better result_df = result_df.sort_values(by='AIC', ascending=True).reset_index(drop=True) return result_df |
特に難しいことはしていない。10行目から14行目で、パラメータを設定し訓練データで訓練する。18行目でAICを取り出し、19行目でresultsに保存する。25行目で昇順にソートする。結果は以下の通り。
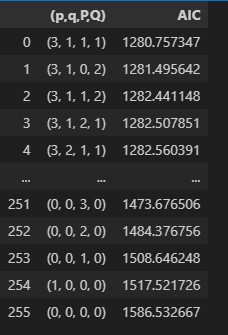
最も小さいAICを与える組が最適なパラメータである。ここでは![]() である。
である。
残差分析
次に、訓練データの残差が自己相関を持つか否かを判定するために、リュング・ボックス検定を行う。この検定の帰無仮説と対立仮説は以下の通りである。
p値が0.05を越える場合、帰無仮説は棄却されない。つまり、データ(今の場合は残差)は自己相関を持たないことになる。この検定は次のコードで実行できる。
|
1 2 3 4 |
from statsmodels.stats.diagnostic import acorr_ljungbox residuals = SARIMA_model_fit.resid result_df = acorr_ljungbox(residuals, np.arange(1, 11, 1)) result_df |
2行目で訓練データの残差を取り出し、3行目の関数acorr_ljungboxでリュング・ボックス検定を行っている。この関数の2つ目の引数は、自己相関を計算するラグの範囲を決めている。今の場合ラグ1からラグ10までの検定を行う。ラグとは自己相関を取る相手までの時間ステップの長さのことである。出力は以下の通り。
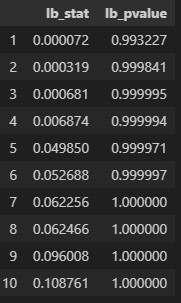
全てのラグにおいてp値(左図のlb_pvalue)は0.05を越えている。つまり、帰無仮説は棄却できず、残差は自己相関を持たないことになる。残差の評価をもう1つ行うため以下のコードを実行する。
|
1 2 3 4 5 |
(p,d,q) = (3,1,1) (P,D,Q,s) = (1,1,1,12) SARIMA_model = SARIMAX(train, order=(p, d, q), seasonal_order=(P,D,Q,s), simple_differencing=False) SARIMA_model_fit = SARIMA_model.fit(disp=False) SARIMA_model_fit.plot_diagnostics(figsize=(10, 8)) |
上のコードは残差が正規分布に従うか否かを見るためのものである。出力は以下の通り。
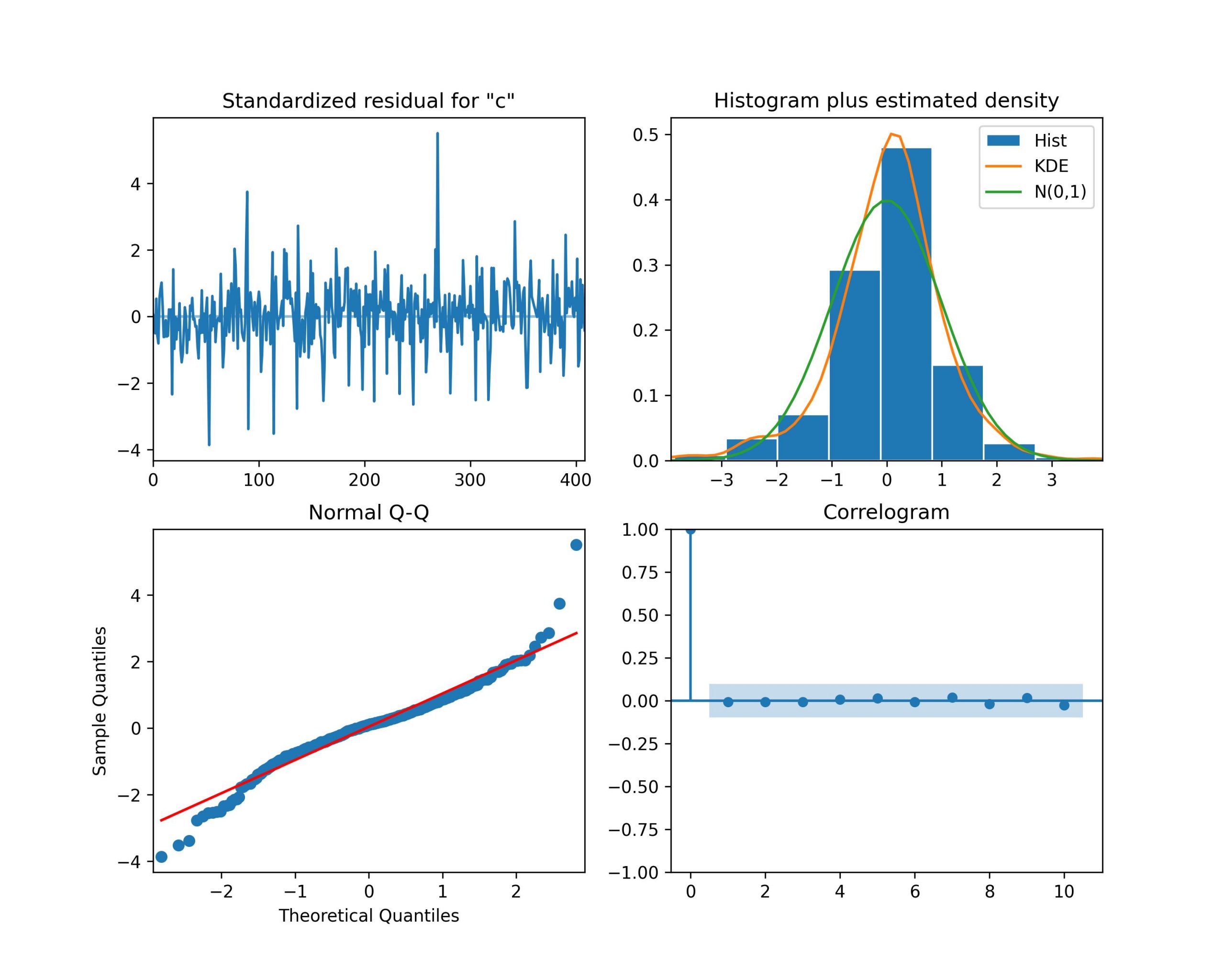
以上より、残差に自己相関はなく、正規分布に従うことを確認できた。つまり、SARIMAモデルが大変よくこのデータを再現できていることを示している。
予測
最後に、テストデータを使い、最近2年間の二酸化炭素濃度を予測する。
|
1 2 |
SARIMA_pred = SARIMA_model_fit.get_prediction(422, 445).predicted_mean test["SARIMA_pred"] = SARIMA_pred |
1行目で予測をしている。訓練データが421ステップまであるから、そこから先の24ステップ(422~445)を計算する。2行目で予測した値をDataFrameのインスタンスtestに格納している。
グラフは以下の通り。
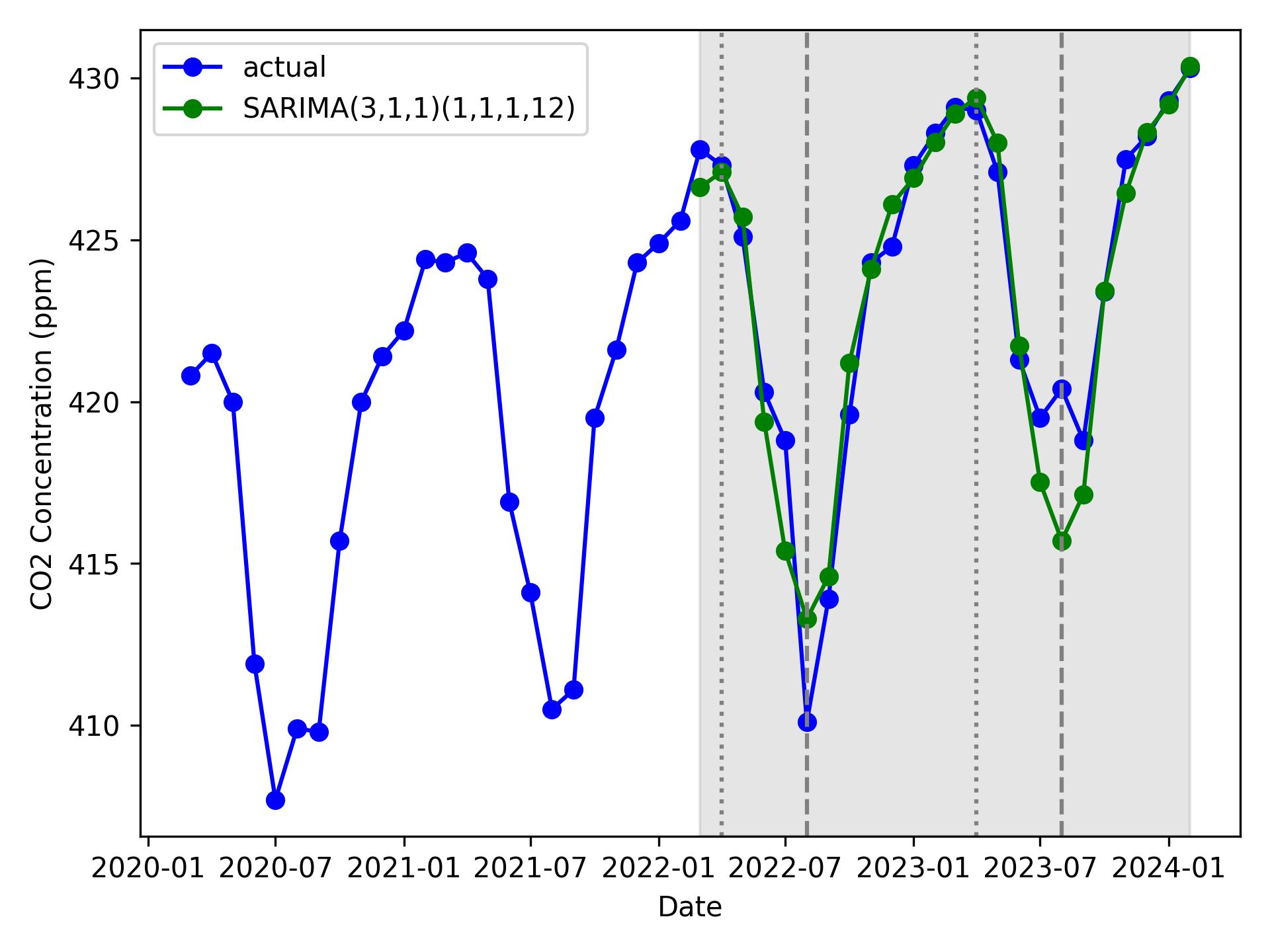
灰色背景の部分が予測した範囲である。青線が実際の値、緑の線が予測値である。垂直な点線は4月を、垂直な破線は8月を表す。予測範囲の平均絶対誤差率を計算する。
|
1 2 |
def mape(y_true, y_pred): return np.mean(np.abs((y_true - y_pred) / y_true)) * 100 |
|
1 2 |
mape_SARIMA = mape(test['co2'], test['SARIMA_pred']) print(mape_SARIMA) |
結果は0.25432273810544875となる。観測値と予測値のずれは0.25%程度であり、大変精度良く予測できていることが分かる。
まとめ
今回は、書籍「Pythonによる時系列予測」の手順に従い、気象庁の時系列データを解析し、大変精度良く予測できることを示した。もちろん、今回はたまたま上手くいっただけかもしれないが、SARIMAモデル(や今回は扱わなかったがARIMAモデル)は十分に実用に耐える予測モデルであると思う。時系列解析における最初の一手として使えるだろう。

