こんにちは、BBです。
今を時めく予測分布とハイパーパラメータのお二人についてご紹介していきます。
この記事の目的は「予測分布についてどういうものなのかイメージがうまくできていないという方がご自身でソースコードに落とし込めるようになる」です。そもそも僕がそうなりたいと思って記事を書いてます。終盤はPythonコードの説明もあります。
予測分布のご紹介
そもそも予測分布とは
そもそも予測分布とはなにかというと、これです。
(1) ![]()
突如として現れた数式に対して動揺を隠しきれませんが、これが現実です。ここで左辺の![]() を予測分布といい、
を予測分布といい、![]() を既に観測されている値、
を既に観測されている値、![]() をパラメータ、
をパラメータ、![]() を未知の値といいます。
を未知の値といいます。![]() のような縦線は
のような縦線は![]() を固定したときの
を固定したときの![]() という意味です。
という意味です。
予測分布の「分布」ってなに?
分布、分布と何度も出てきていますがこれはいったい何なのでしょうか。ここでいう分布とは「全部足したら1になる数字の並び」です。例えば![]() こんな感じです。
こんな感じです。![]() これでもいいです。合計が1になる数字の並び、簡単ですね。
これでもいいです。合計が1になる数字の並び、簡単ですね。![]() だの
だの![]() だのといった個々の数値のことを「確率」といい、この分布のことを「確率分布」と言ったりします。よく知られている確率は合計が100%ですが、合計が100なのか1なのか程度の違いしかないので同じものとします。
だのといった個々の数値のことを「確率」といい、この分布のことを「確率分布」と言ったりします。よく知られている確率は合計が100%ですが、合計が100なのか1なのか程度の違いしかないので同じものとします。
さて、分布について説明してきましたが![]() で表される予測分布も同じことです。この確率分布は
で表される予測分布も同じことです。この確率分布は![]() のように
のように![]() で書かれることが多いです。カッコの中には
で書かれることが多いです。カッコの中には![]() が入っているので変数
が入っているので変数![]() になんかすると出てくる答えを、全パターン並べると上記の「確率分布」になっていることを示しています。注意したいのは
になんかすると出てくる答えを、全パターン並べると上記の「確率分布」になっていることを示しています。注意したいのは![]() に適当な値を入れると出てくるのは
に適当な値を入れると出てくるのは![]() がその値をとりうる確率となっています。例えば
がその値をとりうる確率となっています。例えば![]() のなかの
のなかの![]() かもしれません。言い換えると変数
かもしれません。言い換えると変数![]() の全パターンの「確率」を並べたのが「確率分布」ということです。
の全パターンの「確率」を並べたのが「確率分布」ということです。
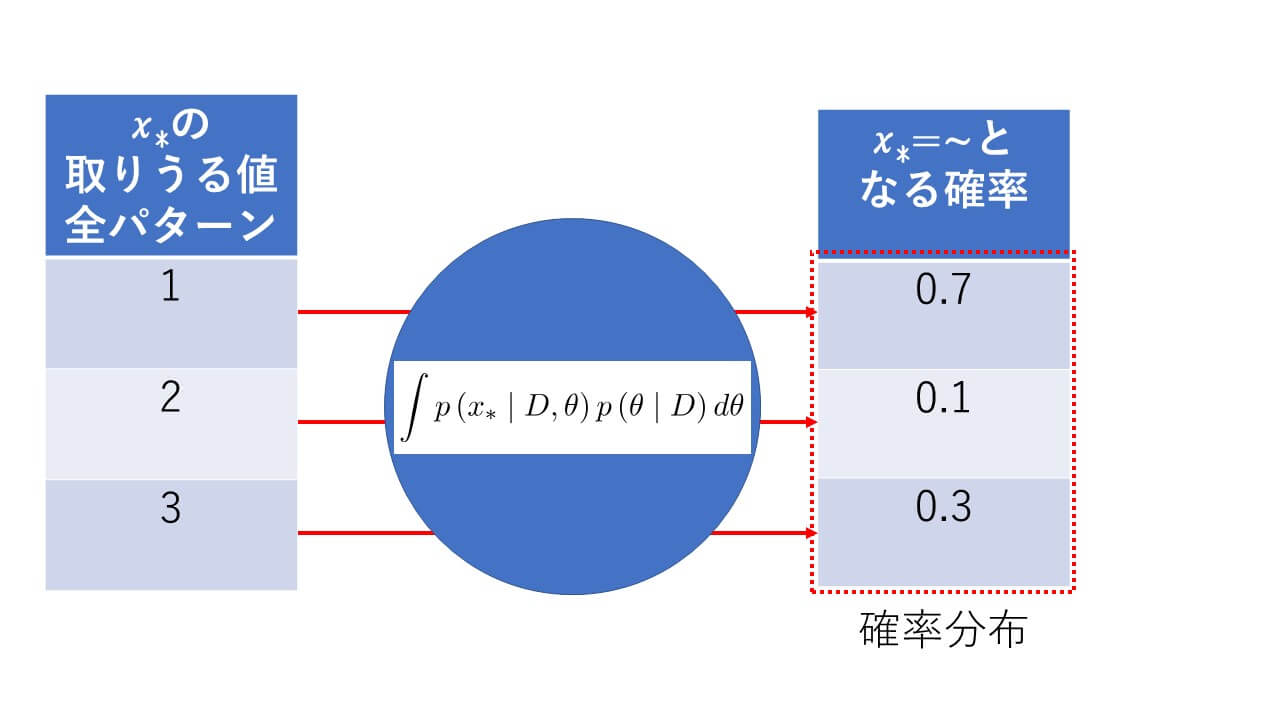
もう一度、予測分布の式を眺めてみる
もう一度、予測分布の式を眺めてみるとすでにお気づきかもしれませんが、めっちゃ使われています![]() が。ここまでの知識で予測分布の式を日本語訳してみます。長いのでまずは積分
が。ここまでの知識で予測分布の式を日本語訳してみます。長いのでまずは積分![]() の中を見てみましょう。
の中を見てみましょう。![]() =>「
=>「![]() を固定したときの
を固定したときの![]() を変数にとる確率と
を変数にとる確率と![]() を固定したときの
を固定したときの![]() の確率をかけたもの」となります。
の確率をかけたもの」となります。![]() は観測した値ですので、すでに固定されていますね。パラメータ
は観測した値ですので、すでに固定されていますね。パラメータ![]() で積分というのは
で積分というのは![]() 全パターンで出てきた値を全部足すということになります。続いて左辺
全パターンで出てきた値を全部足すということになります。続いて左辺![]() =>「
=>「![]() を固定したときの
を固定したときの![]() となる確率」つまり観測値をこの式に突っ込んでやると今後起こりうる事象の確率が予測できてしまうということです。さすが予測分布。名前に恥じない働きをしてくれそうです。
となる確率」つまり観測値をこの式に突っ込んでやると今後起こりうる事象の確率が予測できてしまうということです。さすが予測分布。名前に恥じない働きをしてくれそうです。

ハイパーパラメータのご紹介の前に
まずはパラメータだろという話
ハイパーなパラメータの前にそもそもパラメータがよくわかってないよという声が焦燥感とともに僕の中にこだましていますので、まずはパラメータのことをもう少しまとめていきましょう。そもそもパラメータって何でしょうか。ゲームとかではよく耳にする単語ですが、現実世界にパラメータが転がっているのを見たことがありませんし、食べたこともありません。そう、パラメータは数値上でのみ存在し、目的のために作られた都合の良い数字というわけです。たいていのものは食べることで認識してきた僕にとってはなかなかとっつき難い代物です。そんな都合の良い数字ですが、その予測分布で使用されるパラメータの目的は「未知の値について何らかの知見を得る」とはっきりしています。要するに「未知の値についての確率分布を求めるために定義した数字」ということになりますね。また、手元にある情報は観測された値![]() だけなのでこれを用いてパラメータ
だけなのでこれを用いてパラメータ![]() を計算していくことになります。
を計算していくことになります。
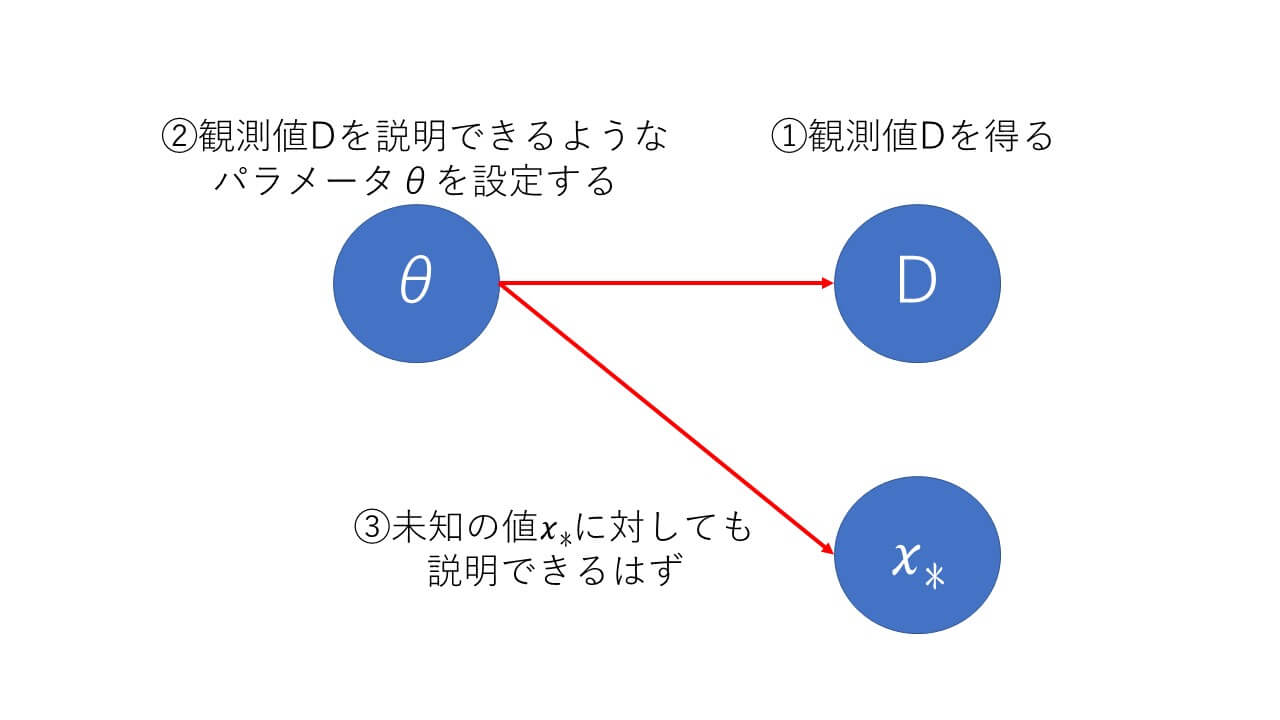
ベイズの定理でパラメータを求めよう
観測された値![]() を用いてパラメータ
を用いてパラメータ![]() を計算する手法、これこそがベイズの定理となります。ベイズの定理についての詳細は別の機会にまとめるとして、パラメータの求め方に注目して整理してきたいと思います。
を計算する手法、これこそがベイズの定理となります。ベイズの定理についての詳細は別の機会にまとめるとして、パラメータの求め方に注目して整理してきたいと思います。
(2) ![]()
こちらがベイズの定理となりますが、いかがでしょうか。すでに式の読み方はばっちりですね!念のため日本語訳していくとこんな感じです。左辺=>「観測された値![]() を固定したときのパラメータ
を固定したときのパラメータ![]() の確率(事後分布)」、右辺=>「”パラメータ
の確率(事後分布)」、右辺=>「”パラメータ![]() を固定したときの観測した値
を固定したときの観測した値![]() の確率”(尤度関数)と”パラメータ
の確率”(尤度関数)と”パラメータ![]() の確率”(事前分布)を掛けて”観測された値
の確率”(事前分布)を掛けて”観測された値![]() の確率(エビデンス)”で割る」となります。パラメータを求めたいのに右辺にやたらとパラメータが入っているので混乱しますが、ここは先人たちの匠の技で何とかなりますので安心してください。
の確率(エビデンス)”で割る」となります。パラメータを求めたいのに右辺にやたらとパラメータが入っているので混乱しますが、ここは先人たちの匠の技で何とかなりますので安心してください。
尤度関数と事前分布と事後分布
式(2)で定義したベイズの定理は問題設定によって適切に尤度関数と事前分布、事後分布を設定してやる必要があります。その前にベイズの定理を使いやすいように少し変形させておきましょう。
(3) 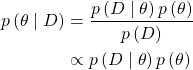
最後の行では分母にあった観測された値![]() の確率、エビデンスが省略されています。求めたい左辺、事後分布は合計が1になる確率分布ですので値そのものにはあまり価値がなく、それぞれの確率の相対的な大小さえ変動がなければ問題ないので固定値となるエビデンスは無視しても問題ないという考え方です。問題によって尤度関数を設定していくのですが、設定した尤度関数に応じて特定の形の事前分布を使用すると事後分布と事前分布が同じ関数形をとることができます。共役事前分布をとるとき左辺の
の確率、エビデンスが省略されています。求めたい左辺、事後分布は合計が1になる確率分布ですので値そのものにはあまり価値がなく、それぞれの確率の相対的な大小さえ変動がなければ問題ないので固定値となるエビデンスは無視しても問題ないという考え方です。問題によって尤度関数を設定していくのですが、設定した尤度関数に応じて特定の形の事前分布を使用すると事後分布と事前分布が同じ関数形をとることができます。共役事前分布をとるとき左辺の![]() と右辺の
と右辺の![]() が同じ式であらわされます。それがどうしたという感じですが、共役事前分布を使うと後ほど紹介しますが逐次学習が効率的に実施できるようになるなど学習を効率化することができます。
が同じ式であらわされます。それがどうしたという感じですが、共役事前分布を使うと後ほど紹介しますが逐次学習が効率的に実施できるようになるなど学習を効率化することができます。
ハイパーパラメータのご紹介
その前に問題設定
さて、ベイズの定理まで説明できましたので具体的に問題を設定して説明していきます。ベイズの定理では問題設定に応じた尤度関数、事前分布、事後分布の設定が必要となるためです。今回はサイコロを投げてどの目が出るかの予測分布を計算したいと思います。そんなものどの目も6分の1になるだろ、と思うかもしれないですが、ここではかなり出来の悪いサイコロを仮定します。そして、そんなことは何も知らないベイズの定理が適切にパラメータを設定できるかが今回の見どころです。
サイコロ問題の尤度関数と共役事前分布
今回の出来の悪いサイコロ問題では確率分布にカテゴリ分布を使います。式にするとこんな感じです。
(4) ![]()
![]() はパラメータ、
はパラメータ、![]() はサイコロの目をベクトルで表現したものになりますが、詳細は後で説明します。カテゴリ分布はサイコロの目のようなきっちり有限個に分類できる事象に対して確率分布を求めることができます。このような確率分布のことを離散確率分布といいます。対して身長が170cmとなる確率のような連続した値を扱うときは連続確率分布といい、このような問題に対しては別の関数を使用します。確率分布がカテゴリ分布の場合は尤度関数にカテゴリ分布、事前分布にディリクレ分布を使います。式(3)に突っ込んでやるとこのようになります。
はサイコロの目をベクトルで表現したものになりますが、詳細は後で説明します。カテゴリ分布はサイコロの目のようなきっちり有限個に分類できる事象に対して確率分布を求めることができます。このような確率分布のことを離散確率分布といいます。対して身長が170cmとなる確率のような連続した値を扱うときは連続確率分布といい、このような問題に対しては別の関数を使用します。確率分布がカテゴリ分布の場合は尤度関数にカテゴリ分布、事前分布にディリクレ分布を使います。式(3)に突っ込んでやるとこのようになります。
(5) 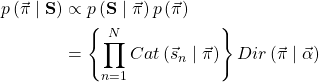
くじけず式の説明をしていきましょう。![]() はパラメータです。パラメータはディリクレ分布で生成しているので要素の和が1になる6次元の実数ベクトルとなります。
はパラメータです。パラメータはディリクレ分布で生成しているので要素の和が1になる6次元の実数ベクトルとなります。![]() は観測値です。サイコロの出た目が観測値ですので出た目の情報が配列の形で入力されます。例えばサイコロを1回振って6が出たらこう。
は観測値です。サイコロの出た目が観測値ですので出た目の情報が配列の形で入力されます。例えばサイコロを1回振って6が出たらこう。
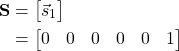
2回振って1と3が出たらこう。

このように1回振ると一つベクトルが追加され、ベクトルは出た目のところに1、他の目は0が入ります。ややこしいですね。式(5)の2行目、![]() が尤度関数のカテゴリ分布、右側が事前分布のディリクレ分布です。この式を変形していくと1行目左辺の事後分布は以下のように事前分布と同じ形をとることが明らかになります。先ほど説明した共役事前分布というわけですね。
が尤度関数のカテゴリ分布、右側が事前分布のディリクレ分布です。この式を変形していくと1行目左辺の事後分布は以下のように事前分布と同じ形をとることが明らかになります。先ほど説明した共役事前分布というわけですね。
(6) 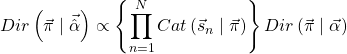
ここで![]() は以下のようなややこしい形になります。
は以下のようなややこしい形になります。![]() は観測値の次元の数となりますので、サイコロの目を考えると
は観測値の次元の数となりますので、サイコロの目を考えると![]() となります。
となります。
(7) 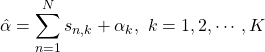
サイコロ問題の予測分布
さて、予測分布の説明を始めます。数式はこれが最後なのでもう少し頑張りますし頑張ってください。サイコロの目問題では尤度関数はカテゴリ分布や共役事前分布はディリクレ分布というようなお約束がありますが、同じように予測分布はカテゴリ分布となります。式(1)と式(3)、式(4)、式(5)を使って以下のように書くことができます。
(8) 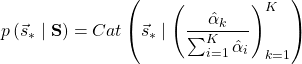
パラメータの形が非常にややこしいことになっておりますが、カテゴリ分布の形をとります。![]() は未知の値、これからサイコロを振って何が出るかを仮定して入力します。つまり右辺に
は未知の値、これからサイコロを振って何が出るかを仮定して入力します。つまり右辺に![]() を与えてやれば6が出る確率が計算できるというわけです。もちろん確率なので
を与えてやれば6が出る確率が計算できるというわけです。もちろん確率なので![]() に1~6の目それぞれを入力して出力された確率は合計1になります。
に1~6の目それぞれを入力して出力された確率は合計1になります。
ハイパーパラメータは適当に決める??
ようやくハイパーパラメータを説明する準備が整いました。今回のサイコロ問題のパラメータは式(5)の![]() が該当します。事前分布であるディリクレ分布の変数を見てみるとパラメータ
が該当します。事前分布であるディリクレ分布の変数を見てみるとパラメータ![]() はいいのですが
はいいのですが![]() を渡すことが前提となっています。これはパラメータを決めるためのパラメータが必要ということになります。つまり超パラメータ、ハイパーパラメータの登場です。サイコロの場合は6個の目がありますので6個のハイパーパラメータを適当に決めてやります。本当に適当でよいのか、非常に疑わしいのでこれから次の章で実験していきましょう。
を渡すことが前提となっています。これはパラメータを決めるためのパラメータが必要ということになります。つまり超パラメータ、ハイパーパラメータの登場です。サイコロの場合は6個の目がありますので6個のハイパーパラメータを適当に決めてやります。本当に適当でよいのか、非常に疑わしいのでこれから次の章で実験していきましょう。
予測分布の計算
予測分布の計算概要
言葉での説明も飽きてきたと思いますのでここからはPythonのコードを混ぜながら予測分布計算プログラムの実装と本当にハイパーパラメータは適当でいいのかを確認していきたいと思います。サイコロは1~10000回振ってそれぞれの結果に対して予測分布を計算しています。処理の流れは以下のような感じで行きます。
- 出来の悪いサイコロデータを生成
- ハイパーパラメータの設定
- パラメータの計算
- 予測分布の計算
出来の悪いサイコロデータを生成する際にどの目がどの確率で出るかを設定するのですが、この設定した確率を予測分布で求めるというのが今回の目的です。もちろん予測分布にはサイコロデータのみをあたえる為、データを作成する際の確率は知る由もありません。
出来の悪いサイコロデータ作成
出来の悪いサイコロを振ってそれぞれの目の出る確率を以下のように定義してみました。出来が悪すぎるので目が出る確率はすべて違っています。
| サイコロの目 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 目が出る確率 | 0.03 | 0.07 | 0.15 | 0.20 | 0.25 | 0.30 |
データを作成するために使用したコードは以下のようになります。
|
1 2 3 4 5 6 7 8 9 10 |
import numpy as np # ランダムを制御 np.random.seed(1) # 出来の悪いサイコロを1~10000回振る saikoro_data = [np.random.multinomial(i+1, [0.03, 0.07, 0.15, 0.2, 0.25, 0.3]) for i in range(1000)] print(saikoro_data) |
saikoro_dataにはサイコロを1~10000回振った結果を格納しています。1回なら1~6の目が何回出たかがそれぞれ[0, 0, 0, 0, 0, 1]、100回なら[ 2, 8, 13, 20, 27, 30]のように順番に入っています。
ハイパーパラメータの設定
値によってどのような影響を見る為、今回はハイパーパラメータを以下1パターンで設定していきます。
| パターンA | [1, 1, 1, 1, 1, 1] |
|---|---|
| パターンB | [11, 22, 33, 44, 55, 66] |
| パターンC | [66, 55, 44, 33, 22, 11] |
値によって計算結果にどのような差が生じるのでしょうか。
パラメータの計算、予測分布の計算
共役事前分布のディリクレ分布を使って![]() を求め、予測分布の計算まで一気に行っていきます。コードはこんな感じのを作りました。
を求め、予測分布の計算まで一気に行っていきます。コードはこんな感じのを作りました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
from matplotlib import pyplot as plt from scipy.stats import multinomial # ハイパーパラメータの設定 pattern = 'a' alpha = [1, 1, 1, 1, 1, 1] # alpha = [11, 22, 33, 44, 55, 66] # alpha = [66, 55, 44, 33, 22, 11] m = np.diag(np.ones(len(saikoro_label_list))) pi = np.random.dirichlet([saikoro_data_list[100][i] + alpha[i] for i in range(6)]) # 1~10000回サイコロを振ったデータを用いて予測分布を計算する pred_list = [] for saikoro_data in saikoro_data_list: # ディリクレ分布を用いたパラメータの計算 pi = np.random.dirichlet([saikoro_data[i] + alpha[i] for i in range(6)]) # カテゴリ分布を用いた予測分布の計算 pred = [multinomial.pmf(i, 1, [p for p in pi]) for i in m] pred_list.append(pred) pred_array = np.array(pred_list) # 作図 plt.plot(np.arange(1, count+1, 1), pred_array[:,0], label='{}_1'.format(pattern)) plt.plot(np.arange(1, count+1, 1), pred_array[:,1], label='{}_2'.format(pattern)) plt.plot(np.arange(1, count+1, 1), pred_array[:,2], label='{}_3'.format(pattern)) plt.plot(np.arange(1, count+1, 1), pred_array[:,3], label='{}_4'.format(pattern)) plt.plot(np.arange(1, count+1, 1), pred_array[:,4], label='{}_5'.format(pattern)) plt.plot(np.arange(1, count+1, 1), pred_array[:,5], label='{}_6'.format(pattern)) plt.xlabel('count') plt.ylabel('pred') plt.ylim(0, 0.7) plt.legend() plt.show() |
まずはパターンAで計算した結果です。
縦軸が確率、横軸がサイコロを投げた回数となっています。
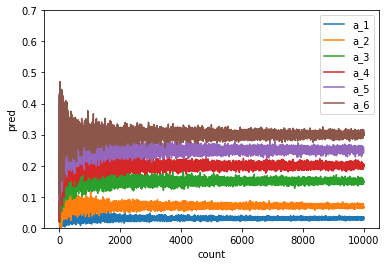
最初はばらつきのあった確率が次第に設定した確率へ収束していく様子がわかります。正しく予測分布が計算できていることがわかりますね。次にパターンBのハイパーパラメータを用いるとどうでしょうか。
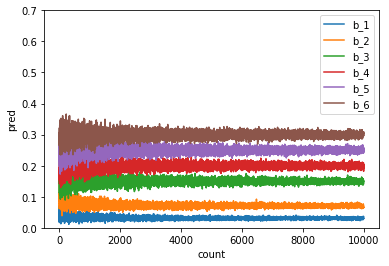
収束の速度に多少変化があるようですが、こちらも正しく予測分布が計算できているように見えます。
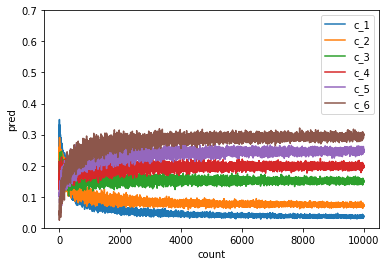
パターンCの結果は他のパターンと同様に収束しますが、初期の値からぐにゃりと曲がって収束しています。収束には他のパターンより多くの観測値が必要になっています。
ハイパーパラメータは適当でよいのか??
今回の実験ではサイコロを10000回振って予測分布の計算を行いました。その結果はどのパターンでも最終的には適切な値に落ち着いています。その点ではハイパーパラメータは適当な値でもよいということになります。これは式(8)で示した予測分布に使用している![]() は観測値の情報を取り込んで精度が改善された為です。
は観測値の情報を取り込んで精度が改善された為です。![]() の定義は式(7)で示していますが観測値
の定義は式(7)で示していますが観測値![]() が含まれていますね。このように観測値が潤沢に準備することができればハイパーパラメータは適当に設定してもいつかは精度が担保されそうです。しかし、観測値が充分に入手できない場合はどうでしょうか。サイコロを振るのに飽きてしまう場合は十分に考えられます。それぞれのパターンでは収束までの回数が異なることは先に述べました。特にパターンCのように本来の確率分布とかけ離れた値を設定してしまうと収束にはより多くの観測値が必要となります。つまり観測値が少ない場合はハイパーパラメータは適当に決めるわけにはいかないというのが結論のようです。
が含まれていますね。このように観測値が潤沢に準備することができればハイパーパラメータは適当に設定してもいつかは精度が担保されそうです。しかし、観測値が充分に入手できない場合はどうでしょうか。サイコロを振るのに飽きてしまう場合は十分に考えられます。それぞれのパターンでは収束までの回数が異なることは先に述べました。特にパターンCのように本来の確率分布とかけ離れた値を設定してしまうと収束にはより多くの観測値が必要となります。つまり観測値が少ない場合はハイパーパラメータは適当に決めるわけにはいかないというのが結論のようです。
共役事前分布のメリット
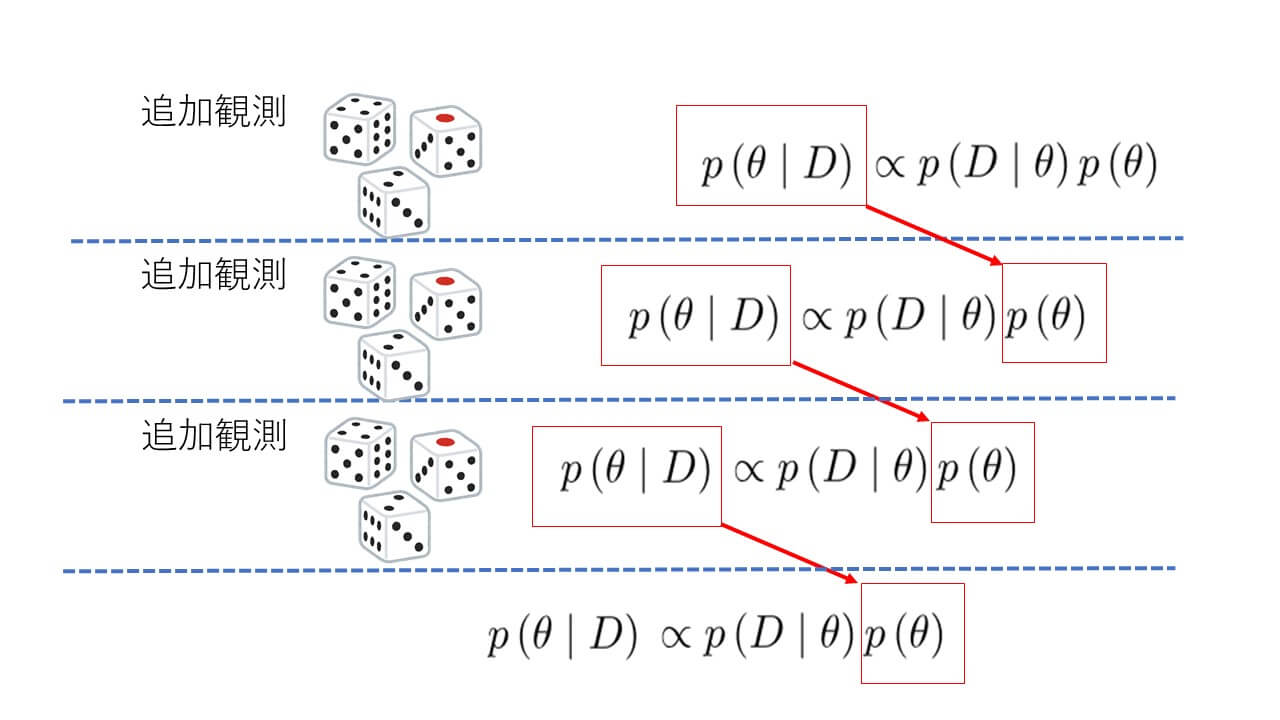
書くのを忘れてましたが、共役事前分布を使った場合のメリットを挙げておきます。サイコロを使った今回の実験でもサイコロを投げれば投げるほど予測精度が向上するという結果を得られましたが、手元にあるデータが充分であるかどうかは計算してみるまで分かりません。もし観測値が足らなかった場合に最初から計算しなおすのは無駄ですよね。そこで共役事前分布の出番です。手持ちの観測値を使って得られた計算結果つまり事後分布を事前分布として式に与えることによって続きから計算できるというわけです。この性質からリアルタイムデータを使った学習も可能になりますね。
まとめ
今回は予測分布とハイパーパラメータと題してまとめてきました。サイコロの目が出る確率を計算するという問題を扱いましたが、結論としては以下のようなことがわかりました。
- サイコロを振れば振るほど予測分布は正解に収束する
- ハイパーパラメータの設定は自由度が高いが、予測分布の収束速度に影響がある場合がある
- 観測値が少ない場合は収束が速くなるようハイパーパラメータの調整が必要となる
ハイパーパラメータの設定によっては収束速度に影響がある為、手元にある観測値が少ない場合は調整する必要がありそうですね。長くなりましたが今回はこの辺でお開きにしたいと思います!

