はじめに
最近の業務で使用したクラスタリングの1手法「DBSCAN」を紹介する。
DBSCAN
クラスタリングとは任意の点の集合(今回は2次元平面の点の集合)を、その分布の仕方に従って複数のクラスタに分割する作業である。複数あるクラスタリング手法の1つがDBSCAN(Density-Based Spatial Clustering of Applications with Noise)だ。DBSCANを実行する際に必要となるパラメータは以下の2つである。
 :ある点からの半径
:ある点からの半径 :半径
:半径 の円内に存在する点の数の最小値
の円内に存在する点の数の最小値
この2つのパラメータを用いて、対象とする各点を以下の3つのいずれかに分類する。
- コア点
- 到達可能点
- 外れ値(ノイズ)
以下で詳細に説明する。
コア点
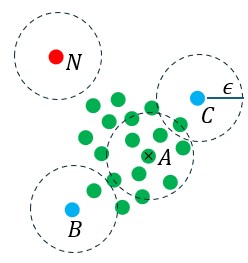
図1
ある点に注目し、その点を中心に半径![]() の円を描く(左図の点線)。その円内に自分自身も含め少なくとも
の円を描く(左図の点線)。その円内に自分自身も含め少なくとも![]() (ここでは4とする)個の点があれば、その点をコア点と定義する。左図では
(ここでは4とする)個の点があれば、その点をコア点と定義する。左図では![]() を含む緑の点は全てコア点である。
を含む緑の点は全てコア点である。
到達可能点
図1の点![]() や
や![]() は半径
は半径![]() の円内に点を持つがその個数は
の円内に点を持つがその個数は![]() 未満である。従ってコア点ではない。しかし、他のコア点(緑)を経由して、お互いに到達することができる。このような点を到達可能点と呼ぶ。点
未満である。従ってコア点ではない。しかし、他のコア点(緑)を経由して、お互いに到達することができる。このような点を到達可能点と呼ぶ。点![]() 近傍のコア点は同じクラスタを構成し、緑の点を介して到達可能な到達可能点も同じクラスタに属すると定義する。従って図の緑と青の点は同じクラスタにに属する。
近傍のコア点は同じクラスタを構成し、緑の点を介して到達可能な到達可能点も同じクラスタに属すると定義する。従って図の緑と青の点は同じクラスタにに属する。
外れ値(ノイズ)
図1の点![]() はコア点でも到達可能点でもない。このような点を外れ値あるいはノイズと定義する。外れ値はどのクラスタにも属さない。到達可能点と外れ値を合わせてノンコア点と呼ぶことがある。
はコア点でも到達可能点でもない。このような点を外れ値あるいはノイズと定義する。外れ値はどのクラスタにも属さない。到達可能点と外れ値を合わせてノンコア点と呼ぶことがある。
対象とする点を以上の3つの点のいずれかに割り振り、クラスタリングを行うのがDBSCANである。名称に「Density-Based」とあるのは、コア点の定義に見るように、局所的な密度を基準にしているためである。また、コア点を介して到達できない点は外れ値(ノイズ)とみなされる点もDBSCANの特長である。これは名称の「with Noise」に示されている。
実験
DBSCANはPythonライブラリscikit-learnがサポートしているのでこれを使い実験を行う。対象とする点の分布は弓なりに配置された2つの点分布である(下図のSamples)。以下に結果を示す。他のクラスタリング手法であるK-meansとG-meansの結果も比較のため示す。今回のソースはここにある。
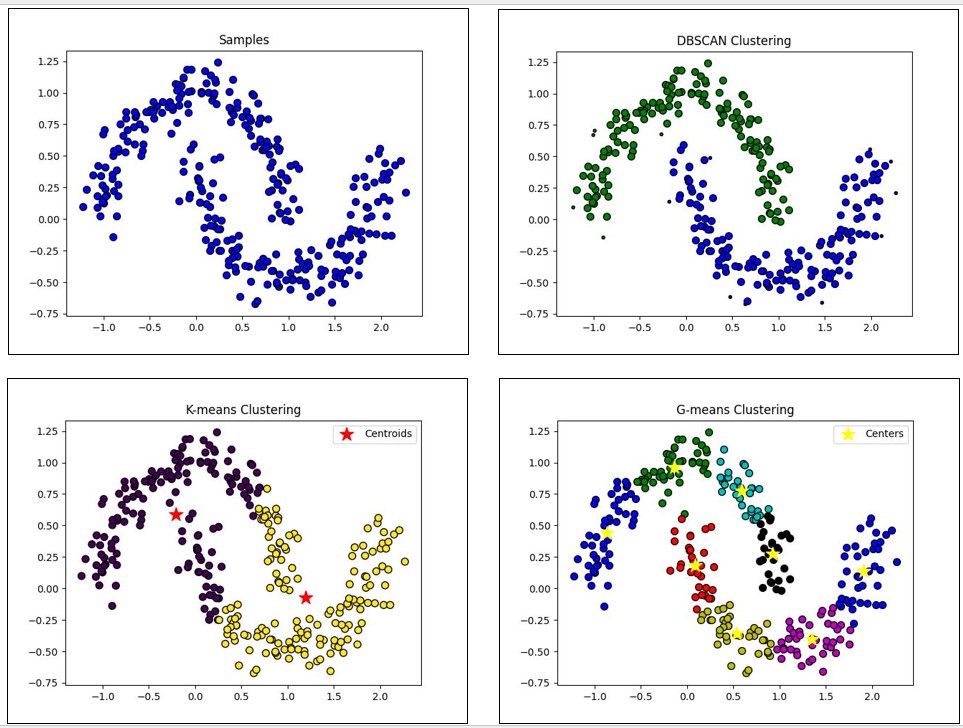
図2
図2上段右がDBSCANによる結果、下段左がK-meansによる結果、下段右がG-meansによる結果である。後者2つについてはクラスタ中心を星印で示した。K-meansではユーザがクラスタ数をあらかじめ決めておく必要があるが、DBSCANとG-meansではクラスタ数は自動的に決まる。上の結果を見ると、K-meansとG-meansでは弓なりの2つの分布を正確に捉えることができていないことが分かる。これら2つの手法はクラスタ中心周りの点の分布を大域的に観察しながら計算を進めるためである(ここではK-meansとG-meansのアルゴリズムの詳細には触れない)。一方、DBSCANでは、先に説明したように、個々の点近傍の密度を見つつ点から点へとたどりながらクラスタが決まっていく。従って、いびつな形状の点分布であっても正確にクラスタリングを行うことができる。今回のサンプルではDBSCANにより外れ値と判定された点は存在しなかった。また、計算速度に関しては、今回の検証では、DBSCANが最も速くK-meansが最も遅かった。DBSCANはK-meansのおおよそ2倍ほどの速さであった。
まとめ
今回は、クラスタリングの1手法であるDBSCANを紹介した。WikipediaのDBSCANの項目を見ると「DBSCAN は最も一般的なクラスタリングアルゴリズムのひとつであり、科学文献の中で最も引用されている。」「2014年、このアルゴリズムは主要なデータマイニングカンファレンスの KDD にて、the test of time award(理論および実践にてかなりの注目を集めたアルゴリズムに与えられる賞)を受賞した。」と書かれている。有名な手法らしいが、恥ずかしながら、今回の案件での調査時に初めて知った手法であった。
クラスタリングは適応される対象ごとに最適な手法が変わるものである。DBSCANも引き出しの1つに加えたい。

