はじめに
CCTが提供している調達DX(調達DX ~見積もり自動化技術~ | CCT)ではAIや3D CADのデータを使用して製造業の見積りの自動化技術を提供しています。
3D CADのデータを3Dプリンターで出力したり切削して作成する際に、加工時間やコストを推測するために体積を計算することがよくあります。
今回は実際にSTLファイルから体積を計算する方法を説明したいと思います。
2次元多角形の面積計算
まずは2次元多角形の面積を計算する方法について考えてみます。
2次元の多角形の面積は、任意の1点と多角形の各辺の2頂点で構成される三角形の面積を足し合わせることで算出します。
この際、多角形の頂点は左回り(反時計回り)に配置されていものとします、
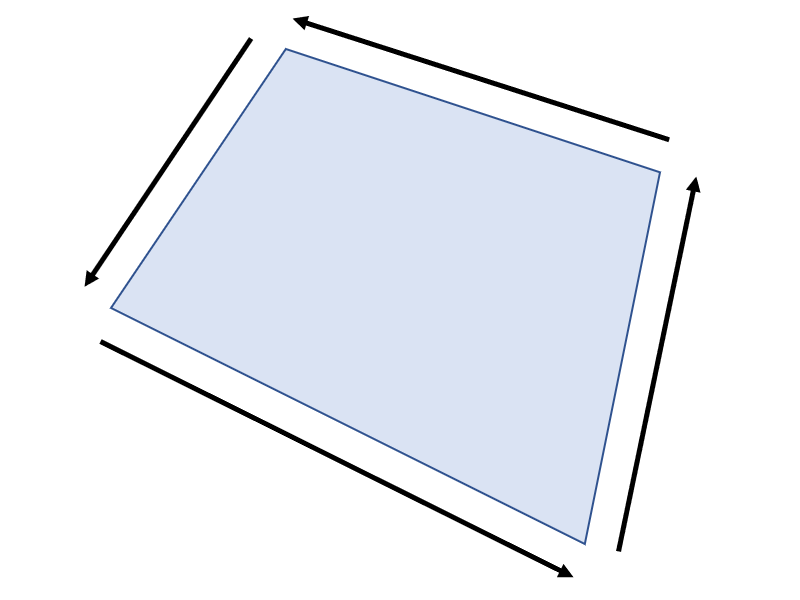
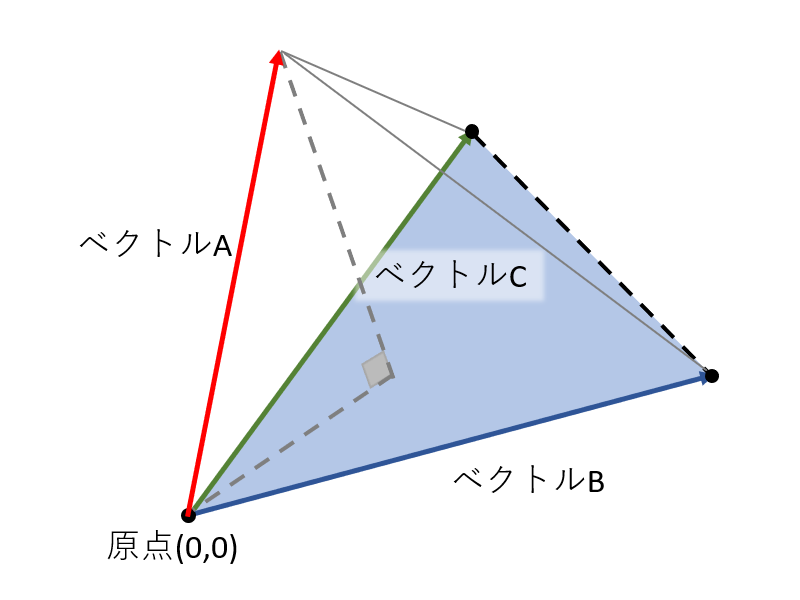
任意の1点を原点(0,0,0)とした場合、三角形の面積Sは点1へのベクトルAと点2へのベクトルBの外積を用いて以下の式で表すことができます。
S = ベクトルA×ベクトルB / 2
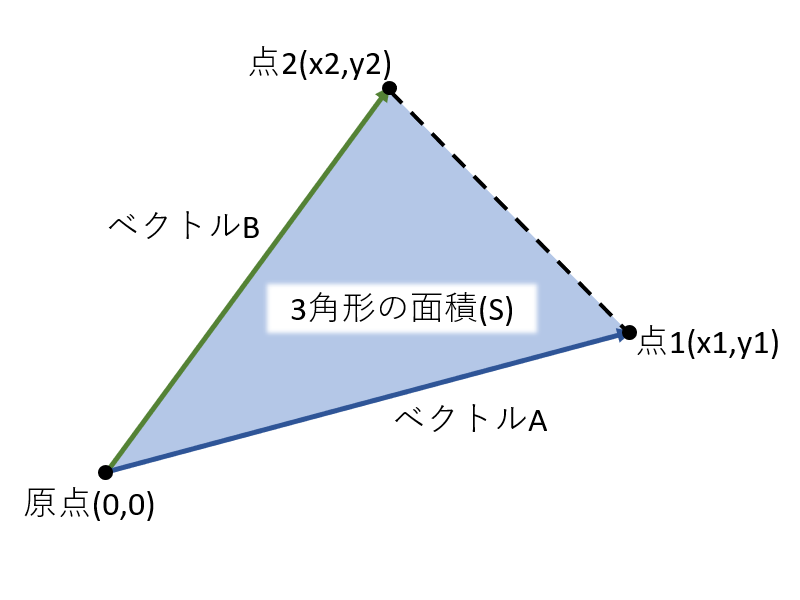
また、ベクトルAを(x1,y1)、ベクトルBを(x2,y2)とすると面積を求める式は次のように表すことができます。
S = (x1y2 – y1x2) / 2
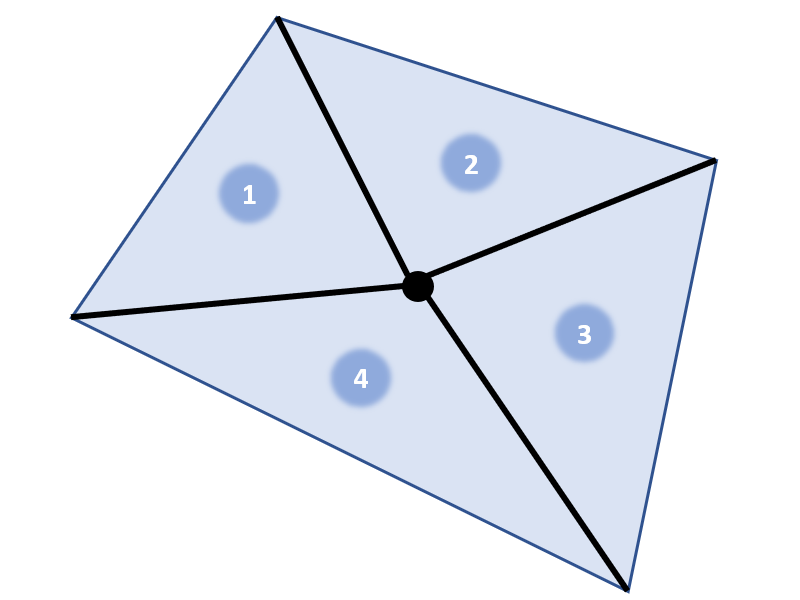
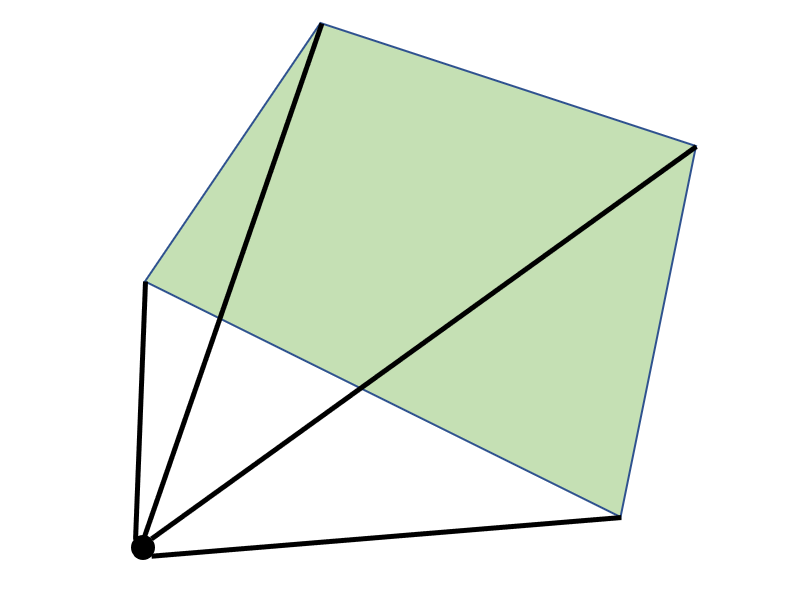
下図の場合は4つの三角形に分割することで三角形1~4の面積の合計が多角形の面積になります。
任意の点が多角形の内側ではなく、外側にある場合はどうなるでしょうか?
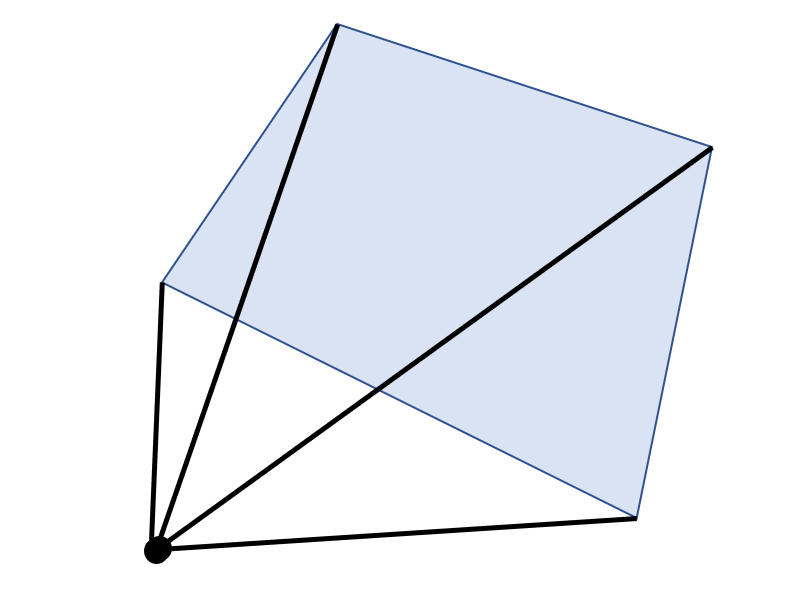
この場合三角形の面積が正になる部分と負になる部分があります。
反時計回りの三角形は面積が正になります。
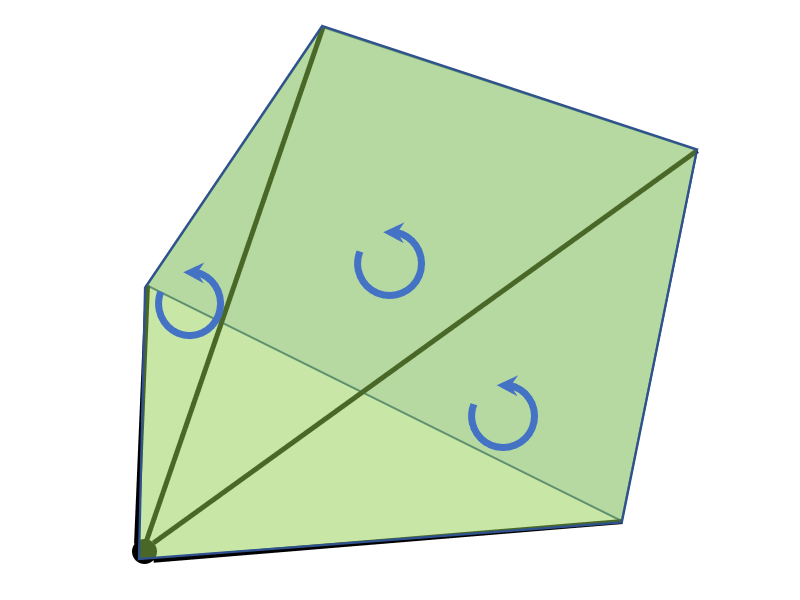
時計回りの三角形は面積が負になります。
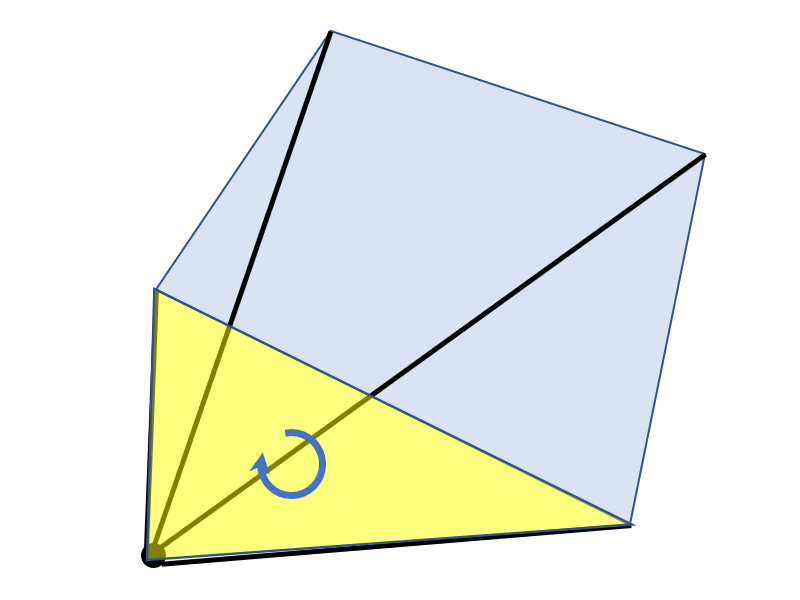
正の面積と負の面積が重なる部分の面積は足し合わすと0になるので、その部分を取り除くと多角形の内側の部分の面積が残ります。
任意の点が多角形の内側でも外側でも面積が正しく算出されることがわかります。
任意の点を原点(0,0,0)にすると計算が簡単になるため、一般的には原点が使用されます。
3次元多角形の体積計算
2次元の面積計算の考え方を用いて3次元のSTLファイルの体積を計算してみます。
三角錐の体積を求める式は以下のように底面積と高さを用いて表します。
三角錐の体積 = 底面積 × 高さ / 3
STLの3つの頂点から作成したベクトルの内積と外積を用いて表すと、三角錐の体積Vを求める式は
V = A ・ ( B × C ) / 6
に、なります。
STLファイルの三角形は表面から見て反時計回りになる規則があります。
任意の点が裏側の場合は体積は正に、表側の場合は体積は負になるため、2次元の時と同様にすべての三角形に対して三角錐の体積を計算して足し合わせることでSTLファイルの体積を求めることができます。
STLファイルの体積計算の注意点
この方法でSTLファイルの体積を求める際に、STLファイルに隙間やエラーがあると期待する値になりません。
まずは、前回のブログで紹介したSTLファイルのエラーチェックを行い、STLファイルの隙間や反転などのエラーを修正しておく必要があります。
まとめ
今回紹介した方法は、複雑なSTLファイルの体積でも個々の三角形で計算した体積を足し合わせることで求めることが可能なため並列計算での高速化なども比較的容易に実装することが可能です。
実際にはCADやSTLのライブライなどで体積計算の機能が提供されており、自分で体積計算のプログラムを作成することは少ないと思いますが、実際にどのような計算が行われているのか知ることで応用的な計算が必要な場合の役に立てばと思います。

