我々が扱っている形状認識とは、3D CADのモデルを解析して製造などに必要な情報を取り出す技術です。
今回は、形状認識に使われる数学の話をしましょう。
形状認識の対象となる3Dモデルは、製品の中に使われる都合や設計者の意図によって方向が決まるので、必ずしも形状認識に都合のよい方向を向いているとは限りません。

そこで、形状認識の過程でモデルを回転させることが、よくあります。
二次元の回転
実際に扱うモデルは三次元ですが、その前に二次元の場合について考えてみましょう。
二次元平面上の点P(x,y)を原点を中心に角度βだけ反時計回りに回転させた点P'(x’y’)を求めたいとしましょう。
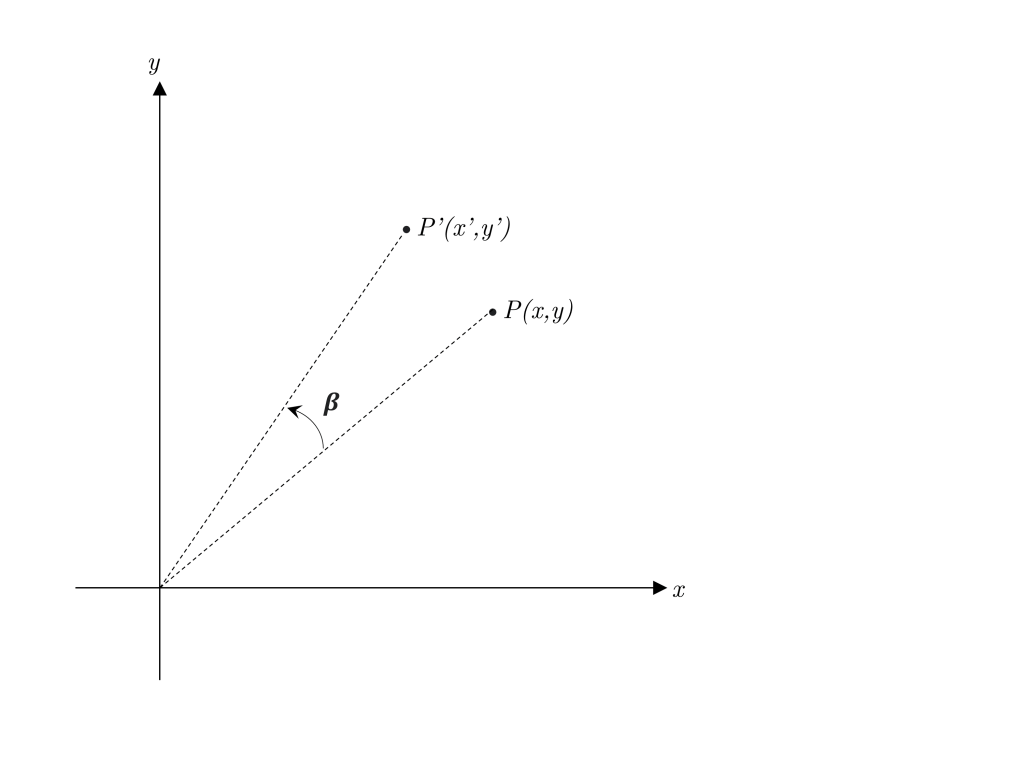
まず、点P(x,y)は、![]() と置くことで、
と置くことで、
![]()
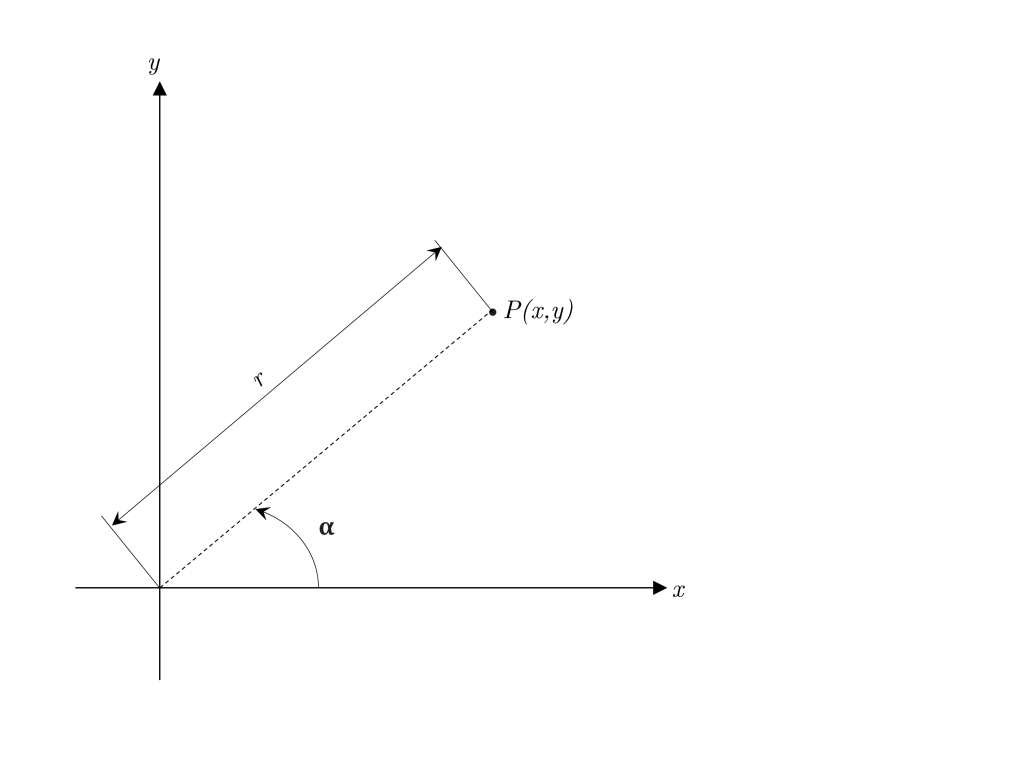
と書き直せます(式1)。![]() が単位円上にX軸から角度αだけ反時計回りに進んだ点の座標を与えることから自明です。
が単位円上にX軸から角度αだけ反時計回りに進んだ点の座標を与えることから自明です。
 求めたい点P’はここからさらに角度βだけ反時計回りに回転させた点なので、その座標は
求めたい点P’はここからさらに角度βだけ反時計回りに回転させた点なので、その座標は![]() になります。そこで加法定理(覚えていますか?)を適用すると、
になります。そこで加法定理(覚えていますか?)を適用すると、
![]()
ここに式1を代入すると、
![]()
(式2)
この式を行列とベクトルの積の形に書き換えて
![]()
(式3)
これが求める答えです。右辺で前乗(前から掛けること)している行列を回転行列と呼びます。
回転という操作が行列の掛け算で表されることがわかりました。
複素平面と回転
ところで複素数というものがありましたよね。二次方程式
![]()
の解
![]()
が、![]() の下では負の数の平方根の計算をしなければならなくなるのを解決するってヤツです。
の下では負の数の平方根の計算をしなければならなくなるのを解決するってヤツです。
どうするかというと、虚数単位iというものを考えて![]() とし、普通の代数式と同じように計算できるものとするのです。
とし、普通の代数式と同じように計算できるものとするのです。
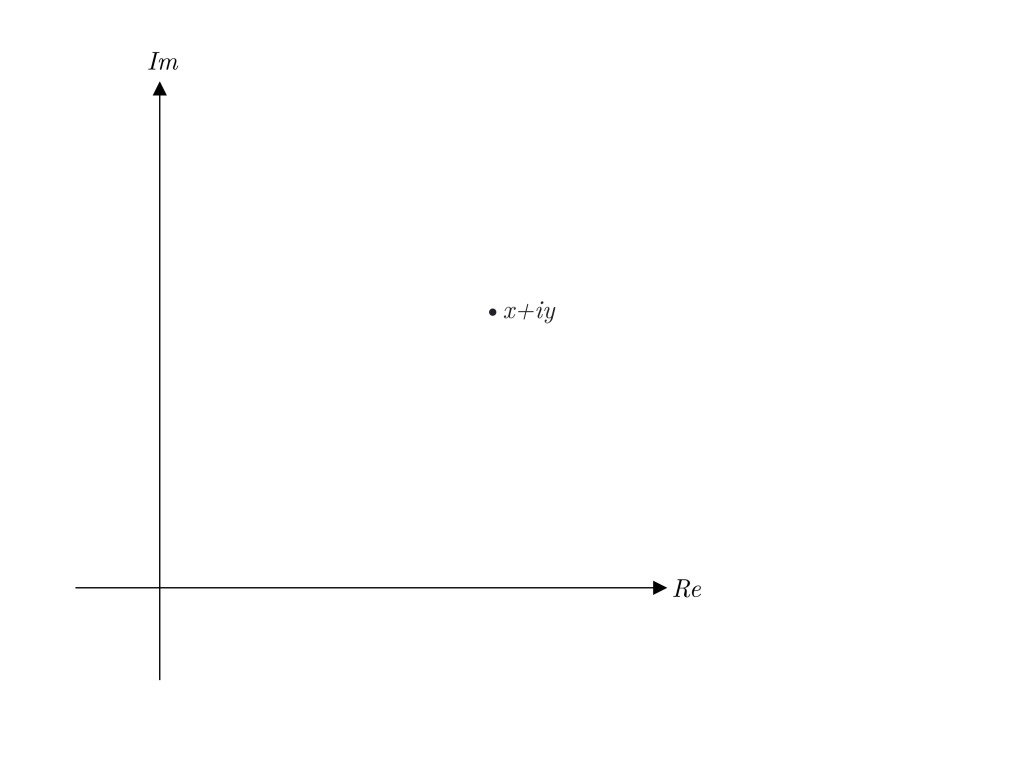
さて。ある複素数![]() を考えた時、iの係数yはこの数自体としては実数部分にはなんら影響を与えないので実数部分の係数xとは無関係に表すことができます。そこで実数部分の係数xを横軸(実軸)、iの係数yを縦軸(虚軸)に取ってプロットすることができます。
を考えた時、iの係数yはこの数自体としては実数部分にはなんら影響を与えないので実数部分の係数xとは無関係に表すことができます。そこで実数部分の係数xを横軸(実軸)、iの係数yを縦軸(虚軸)に取ってプロットすることができます。
ここで(わざとらしいですが)複素数![]() と
と![]() の積を考えてみましょう。
の積を考えてみましょう。
![]()
よく見てみるとこの式は式2とまったく同じ形をしてますね。つまり、![]() という複素数を掛けると、複素平面上で反時計回りに角度β回転させることになるのです。
という複素数を掛けると、複素平面上で反時計回りに角度β回転させることになるのです。
先に求めた行列と同じ働きですね。
このふたつのやり方、複素数と行列による回転は1989年から1998年までの短い間、高校数学の指導要領に入っていました。
わたしも幸いこの期間に高校生だったので、両方のやり方を学ぶ機会があったのですが、片方しか習ってない方も多いのではないでしょうか。
三次元への拡張
我々が形状認識で扱うのは二次元の図面ではなく、三次元のモデルです。
なので三次元空間への拡張を考えてみましょう。
と言ってもそんなに難しい話ではありません。二次元平面は三次元空間の中のz=0なるいち平面ですから、原点を中心とした回転は実はz軸を中心とした回転と見做せます。
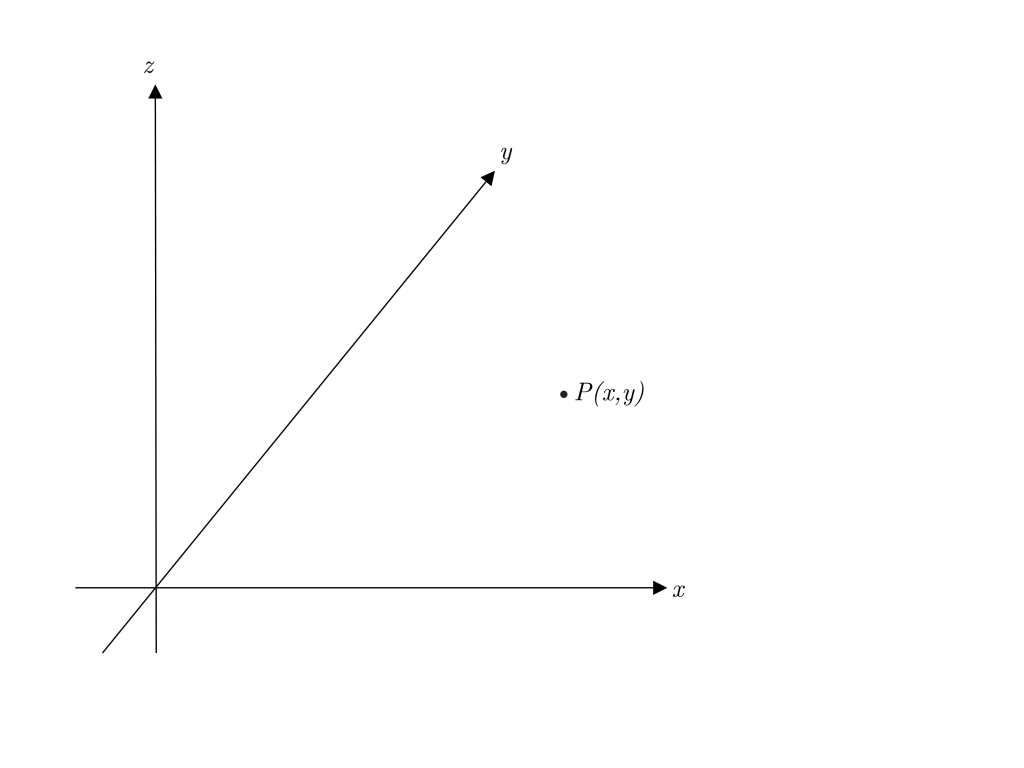
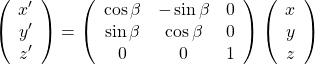
この式は元の点のz座標が回転後もx座標やy座標の影響を受けず変わらないことを表しています。
では他の軸、x軸やy軸を中心とした回転はどうでしょうか。今はz軸の矢印の先から反対方向を眺めるようにしてx-y平面上の回転から式を求めたので、同様にx軸を中心とした回転はx軸の矢印の先から反対方向を眺めるようにして、y軸を中心とした回転はy軸の矢印の先から反対方向を眺めるようにして、それぞれ二次元の回転を考えることで求めることができます。ただし、y軸を中心とした回転を考えるときは、矢印の向きが他の方向とは逆になる軸があるので符号に注意が必要です。
このようにして求めたx軸周り・y軸周り・z軸周りの回転を組み合わせることで、あらゆる方向への回転を表すことができます。
3つの軸周りの角度の組で回転を表す方法を、オイラー角と呼びます。
このように形状認識では、高校までで習うような数学が出てきます。
「三角関数など何の役に立つのだ」といった意見をよく目にするのですが、形状認識には立派に役に立ちます。
学校で習ったことが活かせる仕事があるのはすばらしいことだと個人的には思います。
ところで。複素数と同じように、三次元の回転もなにかの数の掛け算で表せないのでしょうか?
実はできるのですが、この話はまたの機会に。

