FRくんとスキーリフト

調達DXを担う部署で働いているFRくんは、大好きなスキーをするためにDXスキー場にやってきました。なるべく高い所から滑りたいFRくんは、リフトに乗って山頂を目指すことにしました。

FRくんがやってきたスキー場は少し複雑な構造になっていて、たくさんのリフトと中継地点が存在しています。山頂に到達するためには、いくつかのリフトを経由しなければなりません。

また、このスキー場のリフトは一定時間おきに発車し、一方向のみ乗車可能です。

具体的には、リフト $\:\:i\:\:$ は地点 $\:\:A_i\:\:$ →地点 $\:\:B_i\:\:$ を $\:\:T_i\:\:$ の時間で結んでおり( $\:\:A_i\:\:$ から $\:\:B_i\:\:$ 方向へのみ乗車可能)、時刻が $\:\:0+n*P_i\:(n\in\mathbb{N})\:\:$ の時に地点 $\:\:A_i\:\:$ を発車します(簡単のために時間の単位を省略しています)。

なるべく長く滑りたいFRくんは、最短時間で山頂まで到達したいです。今を時刻 $\:\:0\:\:$ とした時、どのリフトに乗れば最短時間で山頂まで到達できるでしょうか？

たくさんのリフトがあります

この問題は、グラフ理論において「2頂点対最短経路問題」と呼ばれています。最短経路問題にはいくつかのアルゴリズムが存在し、適切に使用することでこの問題を解くことが可能です。

具体例を考えてみましょう。以下の状況を仮定します。

中継地点の数： $6$ 　リフトの数： $10$

リフト番号(1～10)	出発地点A	到着地点B	所要時間T	発車間隔P
リフト1	麓(スタート地点)	中継地点1	10	3
リフト2	中継地点1	中継地点2	9	7
リフト3	中継地点1	中継地点3	12	19
リフト4	中継地点2	中継地点3	5	3
リフト5	中継地点3	中継地点4	15	6
リフト6	中継地点3	中継地点6	17	11
リフト7	中継地点2	中継地点5	12	11
リフト8	中継地点5	中継地点6	13	4
リフト9	中継地点4	山頂(ゴール地点)	7	7
リフト10	中継地点6	山頂(ゴール地点)	9	15

この状況をグラフで表現してみます。まず各地点を頂点とみなし、各頂点番号を各地点の番号と対応させます。この時、スタート地点の頂点番号を $0$ 、ゴール地点の頂点番号を $7$ とします。

次に辺の引き方を検討します。出発地点から到着地点に向かって所要時間を重みとした辺を引けば良さそうです。また今回はリフトの経路が片道であるため、有向グラフとして表現します。

これらの考察により、以下のグラフが構築できます。

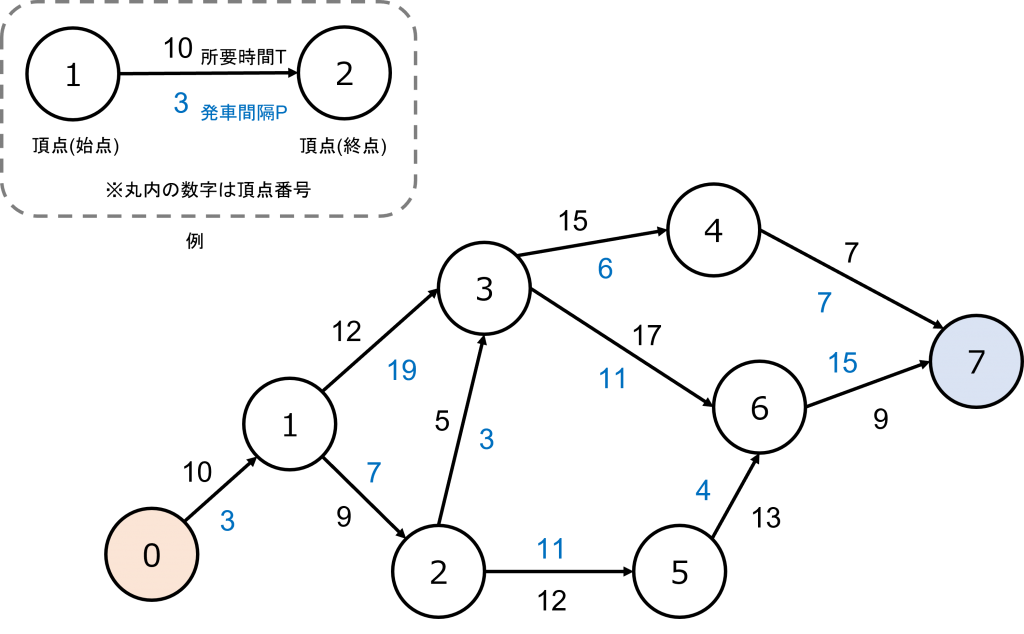
麓(スタート地点)は橙、山頂(ゴール地点)は青で着色しています

グラフを用いることで、状況を整理することができました。

ここで、上記のグラフには負の重みが存在しない(=負辺が存在しないと表現します)ことが分かります。負辺が存在しないことは、最短経路問題を解くアルゴリズムを選ぶために大切な情報の1つです。

上記のグラフにおいて、今回解きたい問題は「FRくんが頂点0から頂点7へ向かう場合の最短経路とその所要時間」になります。

負辺が存在しないグラフにおいて、2頂点対最短経路を求めるためのアルゴリズムの1つに「Dijkstra(ダイクストラ)法」があります(Wikipedia)。計算量は、heap構造を使用し適切に枝刈りを行った場合に $O(V+|E|log|V|)$ となります( $E$ ：辺の本数、 $V$ ：頂点の数)。ダイクストラ法のアルゴリズムの詳細についてはここでは割愛します。詳しくは上記に添付したリンクまたは以下のC++による実装をご覧下さい。

また各地点において、リフトは発車間隔 $P$ で稼働してします。このため、FRくんは各地点においてリフトの出発時間まで待機してから次の地点へ移動しなければなりません。この時、移動先への到着時刻 $arrival\_time$ は、FRくんがある地点に到着した時間を $now\_time$ 、その地点から乗ることができるリフトの発車間隔 $P$ を $now\_p$ 、移動先への所要時間を $now\_weight$ とすると以下の式で計算できますは( ⌈ ⌉ は床関数です)。

$arrival\_time=\lceil now\_time/now\_p \rceil *now\_p+now\_weight$

これでFRくんの移動に関する考察は全て終了しました。最短経路を復元するための配列 $previous$ を用意しつつダイクストラ法を実装すると以下のようになります(C++を使用しています)。

#include <iostream>
#include <vector>
#include <queue>
#include <utility>
#include <algorithm>
#include <cmath>

constexpr int V_MAX=200; //今回は頂点の最大個数を200とする
int N, M, A, B, T, P;

struct Edge {
    int to;
    int weight;
    int p;
};

std::vector<Edge> Graph[V_MAX]; 
std::vector<int> Time;
std::vector<int> previous;
std::vector<int> path;

void dijkstra(const int s) {
    Time.resize(N, INT_MAX);
    previous.resize(N, -1);
    std::priority_queue<std::pair<int,int>, std::vector<std::pair<int,int>>, std::greater<std::pair<int,int>>> pq;
    Time[s] = 0;
    pq.push(std::make_pair(Time[s], s));
    while (!pq.empty()) {
        const auto d = pq.top().first;
        const auto from = pq.top().second;
        pq.pop();
        if (Time[from] < d)
            continue;
        for (const auto &u : Graph[from]) {
            const auto[now_to, now_weight, now_p] = u;
            const auto arrival_time = ((Time[from]+now_p-1)/now_p)*now_p+now_weight;
            if (Time[now_to] > arrival_time) {
                Time[now_to] = arrival_time;
                previous[now_to] = from;
                pq.push(std::make_pair(Time[now_to], now_to));
            }
        }
    }
}

std::vector<int> get_result_path(const int goal) {
    std::vector<int> path;
    for (int now = goal; now != -1; now = previous[now]) {
        path.push_back(now);
    }
    std::reverse(path.begin(), path.end());
    return path;
}

int main() {
    std::cin >> N >> M;
    int start = 0, goal = N-1;
    for (int i = 0; i < M; i++) {
        std::cin >> A >> B >> T >> P;
        Graph[A].push_back({ B, T, P });
    }
    dijkstra(start);
    const auto time = Time[goal];
    std::cout << "The total Time is : " << time << std::endl;
    std::cout << "The shortest path is : ";
    for (const auto& p : get_result_path(goal)) {
        std::cout << p << " ";
    }
    std::cout << std::endl;
    return 0;
}

#include <iostream>

#include <vector>

#include <queue>

#include <utility>

#include <algorithm>

#include <cmath>

constexpr int V_MAX=200; //今回は頂点の最大個数を200とする

int N, M, A, B, T, P;

struct Edge {

int to;

int weight;

int p;

};

std::vector<Edge> Graph[V_MAX];

std::vector<int> Time;

std::vector<int> previous;

std::vector<int> path;

void dijkstra(const int s) {

Time.resize(N, INT_MAX);

previous.resize(N, -1);

std::priority_queue<std::pair<int,int>, std::vector<std::pair<int,int>>, std::greater<std::pair<int,int>>> pq;

Time[s] = 0;

pq.push(std::make_pair(Time[s], s));

while (!pq.empty()) {

const auto d = pq.top().first;

const auto from = pq.top().second;

pq.pop();

if (Time[from] < d)

continue;

for (const auto &u : Graph[from]) {

const auto[now_to, now_weight, now_p] = u;

const auto arrival_time = ((Time[from]+now_p-1)/now_p)*now_p+now_weight;

if (Time[now_to] > arrival_time) {

Time[now_to] = arrival_time;

previous[now_to] = from;

pq.push(std::make_pair(Time[now_to], now_to));

}

std::vector<int> get_result_path(const int goal) {

std::vector<int> path;

for (int now = goal; now != -1; now = previous[now]) {

path.push_back(now);

}

std::reverse(path.begin(), path.end());

return path;

}

int main() {

std::cin >> N >> M;

int start = 0, goal = N-1;

for (int i = 0; i < M; i++) {

std::cin >> A >> B >> T >> P;

Graph[A].push_back({ B, T, P });

}

dijkstra(start);

const auto time = Time[goal];

std::cout << "The total Time is : " << time << std::endl;

std::cout << "The shortest path is : ";

for (const auto& p : get_result_path(goal)) {

std::cout << p << " ";

}

std::cout << std::endl;

return 0;

}

先ほどの例を試してみましょう。各値を打ち込んで実行すると結果は以下のようになります。

The total Time is : 56
The shortest path is : 0 1 2 3 4 7

地点0(麓)→中継地点1→中継地点2→中継地点3→中継地点4→地点7(山頂)と移動するのが良いようです。確認してみましょう。各リフトの発車間隔 $P$ に注意すると以下になります。

利用経路	出発時刻	到着時刻
麓→中継地点1	3(0~3は待機)	13
中継地点1→中継地点2	14(13~14は待機)	23
中継地点2→中継地点3	24(23~24は待機)	29
中継地点3→中継地点4	30(29~30は待機)	45
中継地点4→山頂	49(45~49は待機)	56

上記の確認結果より、プログラムは合っていそうです！乗るべきリフトが分かったFRくんはとても笑顔になりました。これでスキーを楽しめそうです。

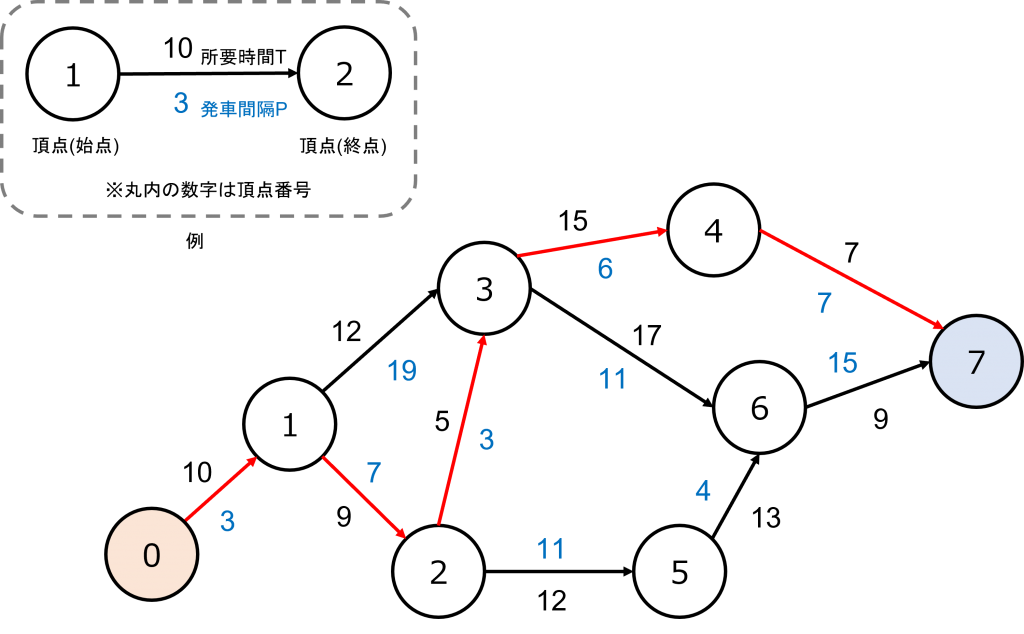
FRくんは赤線の経路を移動すれば良いです

日常生活において、グラフ構造を用いると見通しが良くなる場面はいくつか存在します。ここまで読んで下さった皆さんも、日常に潜むグラフ構造を探してみると面白いかもしれません。

このアルゴリズムは $\:\:N=10^5$ 、 $M=10^5\:\:$ 程度ならば2~3secで計算可能です。スキーリフトが10万個あるスキー場でも、FRくんは山頂までの経路を高速に知ることができます。

男性育休インタビュー

量子位相推定

FRくんとスキーリフト

最近の記事

時系列解析-1（MA過程）

ChatGPTがもたらす哲学の再構築

【モンテカルロ法】ビュフォンの針の問題

AICとBIC

Deep C# vol.2 – record struct

マジックナンバー70

毎月アルゴリズム – 第7回 –

毎月アルゴリズム – 第1回 –

毎月アルゴリズム – 第2回 –

毎月アルゴリズム – 第5回 –

FRくんのお皿洗い(Mr.FR washes the dishes)

【モンテカルロ法】プログラミングで円周率を求める方法

Google Vision APIでOCR

アーカイブ

カテゴリー